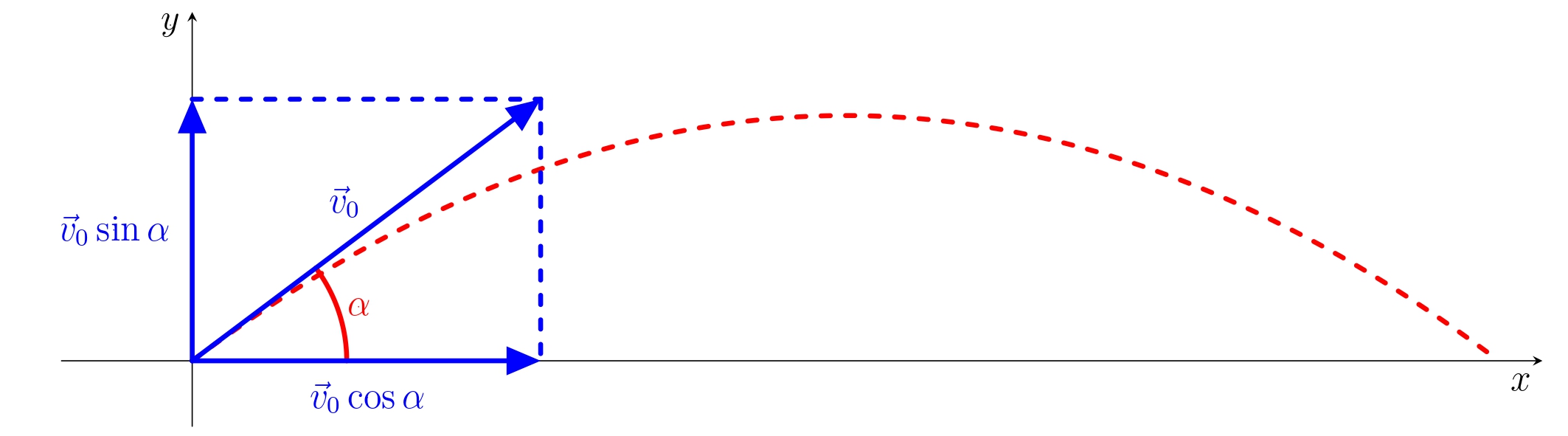
Projectile motion is the most general way of setting an object in a homogeneous gravitational field into motion. Suppose that a body (point mass) is thrown obliquely into space without resistance. The initial velocity is \(\vec{v}_0\) and the angle between the vector \(\vec{v}_0\) and horizontal direction is \(\alpha\). Let us introduce the Cartesian coordinate system with horizontal \(x\)-axis and vertical \(y\)-axis as shown in the picture. The coordinates of the initial velocity vector are
\[\vec{v}_0=(v_0\cos\alpha,v_0\sin\alpha).\]
The motion of the body is governed by an acceleration due to gravity \(g\) directed vertically downwards. The horizontal component of the gravitational acceleration is zero, therefore the motion in the horizontal direction is unaffected by the gravitational field. The vertical component of the motion is affected by the negative acceleration \(-g\). Hence, it is a movement with constant (uniform) deceleration and initial velocity \(v_0t\sin\alpha\).
We can use formulas for distance of motion with constant speed and constant acceleration to quantify the coordinates of the point mass. By doing so we get \[ \begin{aligned} x(t) &= v_0 t\cos\alpha,\\ y(t) &= v_0t\sin\alpha-\frac{1}{2}gt^2. \end{aligned}\tag{1} \]
A golfer hits a ball with an initial velocity \(v_0\). The angle between the initial velocity and the horizontal plane is \(\alpha\). Let’s assume that the drag force is negligible. The motion of the ball therefore satisfies the conditions for movement of a projectile launched at an angle in an environment without air resistance.
Exercise 1. Prove that the trajectory of the golf ball follows a parabolic path.
Solution. To find the equation of the trajectory in the form \(y=f(x)\) it is necessary to eliminate the parameter \(t\) from the system (1).
We solve the first equation with respect to time \(t=\frac{x}{v_0\cos\alpha}\) and substitute into the second equation: \[y(x) = v_0\sin\alpha\,\frac{x}{v_0\cos\alpha} -\frac{1}{2}g\frac{x^2}{v_0^2\cos^2\alpha}= -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .\] From here we see that the \(y\)-coordinate of the trajectory is a quadratic function of the \(x\)-coordinate and the trajectory of the golf ball is therefore described by a parabola.
Exercise 2. Calculate the height of the throw, i.e. the maximal height \(y_{max}\) that the launched ball reaches.
Solution. The height of the throw (projectile motion) is the maximum of the function from the previous exercise: \[f\colon y = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .\]
We calculate the derivative of the function \(f\) as
\[ y'=-\frac{g}{2v_0^2\cos^2\alpha}\cdot2x+\frac{\sin\alpha}{\cos\alpha}\ . \] To find the stationary point, we set the derivative equal to zero and obtain the equation \[ \frac{g}{v_0^2\cos^2\alpha}\cdot x=\frac{\sin\alpha}{\cos\alpha}\ . \] The solution of this equation is \[ x_{max}=\frac{v_0^2\sin\alpha\cos\alpha}{g}\ . \] Since the trajectory of the motion is a concave down quadratic function, the located stationary point is the maximum and the vertical coordinate of this point is the height of the throw.
The height of the throw is calculated by evaluating the function \(f\) at the obtained coordinate \(x_{max}\): \[y_{max}=\frac{v_0^2\sin^2\alpha}{2g}\ .\]
Exercise 3. Given constant initial velocity, find the angle \(\alpha\) which guarantees maximal distance between the initial and the terminal point of the trajectory.
Solution. To find the maximum range angle we need to obtain the terminal point \(x_d\) of the trajectory as a function of the angle \(\alpha\) and find the maximum of the function \(x_d(\alpha).\) Given that \(y=0\) when the ball hits the ground, we find zeros of the function \[y(x) = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x.\] From here we obtain: \[0 = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ ,\] \[0 = x\cdot\left(-\frac{g}{2v_0^2\cos^2\alpha}\cdot x+\frac{\sin\alpha}{\cos\alpha}\right)\ .\] This factorized equation has two solutions. The first solution \(x=0\) corresponds to the place where the ball is launched and the second solution \(x_d\) to the place of impact \[x_d(\alpha) = \frac{2v_0^2\sin\alpha\cos\alpha}{g}=\frac{v_0^2}{g}\sin2\alpha\ .\] Now we need to find the maximum of the function \(x_d(\alpha)\). It is sufficient to find the stationary point, since it has been showed that the trajectory is a parabola that opens downward. We calculate the derivative of the function \(x_d(\alpha)\) with respect to \(\alpha\)
\[x_d'(\alpha)=\frac{v_0^2}{g}\cdot\cos2\alpha\cdot 2\ .\]
By setting the derivative equal to zero, we get \(\cos2\alpha=0\), which is satisfied for \(2\alpha=90^\circ\) (for the ball to be launched, obviously \(\alpha\in\langle0^\circ,90^\circ\rangle\), so the solution is unambiguous). Thus the stationary point is \(\alpha=45^\circ\).
The maximum range in golf is achieved when hitting the ball at an angle \(\alpha=45^\circ\) and the ball lands at a distance of \[x_d(45^\circ) =\frac{v_0^2}{g}\sin(2\cdot45^\circ)=\frac{v_0^2}{g}.\]
Note that it is possible to obtain the function \(x_d(\alpha) = \frac{v_0^2}{g}\sin2\alpha\) without calculus by using the symmetry of the parabola. The vertex of the parabola is located in the middle of the zero points. Therefore, the \(x\)-coordinate of the impact point can be quantified as \(x_d(\alpha) = 2\cdot x_{max}\).
This allows us to avoid solving the quadratic equation obtained by substituting \(y=0\) into the function \(y(x)\) and factorizing the right-hand side.