Odpal golfovej loptičky
 30 min.,
30 min.,  3/3
3/3 Šikmý vrh
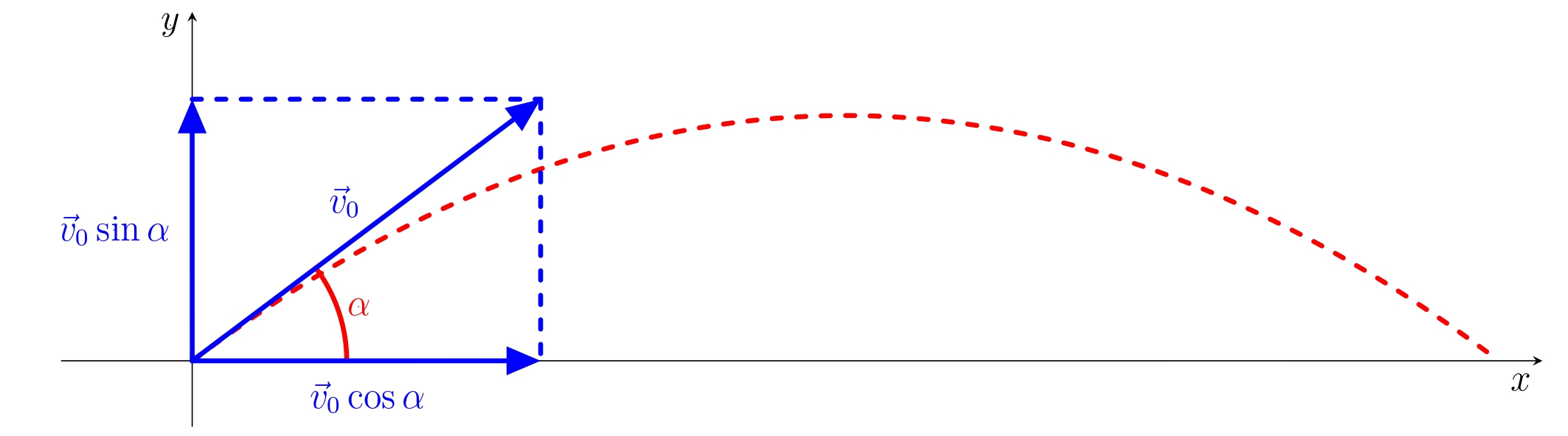
Šikmý vrh je najvšeobecnejší spôsob uvedenia telesa do pohybu v homogénnom ťiažovom poli. Predpokladajme, že teleso (hmotný bod) je vrhnuté šikmo do priestoru bez odporu. Počiatočná rýchlosť je \(\vec{v}_0\) a zviera s vodorovnou rovinou uhol \(\alpha\). Zavedieme karteziánsky súradnicový systém s vodorovnou osou \(x\) v smere vrhu a osou \(y\) zvislou nahor, ako je znázornené na obrázku. Počiatočnú rýchlosť \(v_0\) rozložíme na zložky vzhľadom na zvolený súradnicový systém:
\[\vec{v}_0=(v_0\cos\alpha,v_0\sin\alpha).\]
Pohyb telesa je ovplyvnený tiažovým zrýchlením \(g\), ktoré smeruje zvislo nadol. Horizontálna zložka tiažového zrýchlenia je nulová, preto pohyb vo vodorovnom smere nie je ovplyvnený tiažovým poľom a horizontálna rýchlosť zostáva konštantná. Zvislá zložka pohybu je ovplyvnená konštantným záporným zrýchlením \(-g\), teda smerom nadol. Ide o pohyb s konštantným spomalením a počiatočnou zvislou rýchlosťou \(v_0\sin\alpha\).
Pre súradnice polohy hmotného bodu bude platiť
\[ \begin{aligned} x(t) &= v_0 t\cos\alpha,\\ y(t) &= v_0t\sin\alpha-\frac{1}{2}gt^2. \end{aligned}\tag{1} \]
Odpal golfovej loptičky
Hráč golfu odpáli loptičku s počiatočnou rýchlosťou \(v_0\), ktorá zviera s vodorovnou rovinou uhol \(\alpha\). Predpokladajme, že odporová sila je zanedbateľná. Pohyb loptičky preto spĺňa podmienky pre pohyb šikmo vrhnutého telesa v prostredí bez odporu vzduchu.
Úloha 1. Dokážte, že trajektória golfovej loptičky (pri zanedbaní odporu vzduchu) je parabola.
Riešenie. Na nájdenie trajektórie využijeme, že je daná tvarom funkcie \(y=f(x)\). Je potrebné odstrániť parameter \(t\) z rovníc určujúcich polohu (1). Z prvej rovnice vyjadríme čas \(t=\frac{x}{v_0\cos\alpha}\) a dosadíme ho do druhej rovnice: \[y(x) = v_0\sin\alpha\,\frac{x}{v_0\cos\alpha} -\frac{1}{2}g\frac{x^2}{v_0^2\cos^2\alpha}= -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .\] Ak si označíme \[A=-\frac{g}{2v_0^2\cos^2\alpha}\] \[B=\frac{\sin\alpha}{\cos\alpha}\] vidíme, že sme získali vzťah v tvare \[ y(x)= Ax^2+Bx, \] čo je rovnica kvadratickej funkcie, kde \(A\neq0 \ \). Keďže trajektória golfovej loptičky je daná tvarom funkcie \(y=f(x)\) môžme povedať, že dráha loptičky je parabola.
Úloha 2. Vypočítajte výšku vrhu, t. j. maximálnu výšku \(y_{max}\), ktorú dosiahne vystrelená loptička .
Riešenie. Pre výpočet výšky vrhu potrebujeme vypočítať maximum funkcie z predchádzajúcej úlohy:
\[f\colon y = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .\]
Vypočítame deriváciu funkcie \(f\)
\[ y'=-\frac{g}{2v_0^2\cos^2\alpha}\cdot2x+\frac{\sin\alpha}{\cos\alpha}\ . \] Na nájdenie stacionárneho bodu položíme deriváciu rovnú nule a dostaneme rovnicu
\[ \frac{g}{v_0^2\cos^2\alpha}\cdot x=\frac{\sin\alpha}{\cos\alpha}\ . \] Riešením tejto rovnice je \[ x_{max}=\frac{v_0^2\sin\alpha\cos\alpha}{g}\ . \] Keďže trajektória pohybu je daná tvarom konkávnej kvadratickej funkcie, nájdený stacionárny bod je maximum a zvislá súradnica tohto bodu je výška vrhu.
Výšku vrhu vypočítame dosadením súradnice \(x_{max}\) funkcie \(f\):
\[y_{max}=\frac{v_0^2\sin^2\alpha}{2g}\ .\]
Úloha 3. Vypočítajte pre aký uhol \(\alpha\) doletí golfová loptička pri konštantnej počiatočnej rýchlosti do maximálnej vzdialenosti
Riešenie. Pre výpočet uhla maximálneho dostrelu potrebujeme získať súradnice \(x_d\) miesta dopadu ako funkciu uhla \(\alpha\) a nájsť maximum funkcie \(x_d(\alpha).\) Keďže \(y=0\), keď loptička dopadne na zem tak dosadíme do funkcie \[y(x) = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\] za \(y\) nulovú výšku a vyriešime získanú rovnicu \[0 = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ ,\] \[0 = x\cdot\left(-\frac{g}{2v_0^2\cos^2\alpha}\cdot x+\frac{\sin\alpha}{\cos\alpha}\right)\ .\] Táto rovnica v súčinovom tvare má dve riešenia. Prvé riešenie \(x=0\) zodpovedá miestu odpalu loptičky a druhé riešenie \(x_d\) miestu dopadu \[ x_d(\alpha) = \frac{2v_0^2\sin\alpha\cos\alpha}{g}=\frac{v_0^2}{g}\sin2\alpha\ . \] Teraz potrebujeme nájsť maximum funkcie \(x_d(\alpha)\). Stačí nájsť stacionárny bod vzhľadom na trajektóriu. Vypočítame deriváciu funkcie \(x_d(\alpha)\) podľa \(\alpha\)
\[ x_d'(\alpha)=\frac{v_0^2}{g}\cdot\cos2\alpha\cdot 2\ . \]
Ak položíme deriváciu rovnú nule, tak dostaneme pre stacionárny bod \(\cos2\alpha=0\), čo je splnené pre \(2\alpha=90^\circ\) (pre odpal loptičky platí \(\alpha\in\langle0^\circ,90^\circ\rangle\), takže riešenie je jednoznačné). Stacionárny bod je teda \(\alpha=45^\circ\).
Maximálny dostrel v golfe dosiahneme pri odpálení loptičky pod uhlom \(\alpha=45^\circ\) a loptička dopadne do vzdialenosti \[ x_d(45^\circ) =\frac{v_0^2}{g}\sin(2\cdot45^\circ)=\frac{v_0^2}{g}. \]
Pripomeňme, že je možné získať funkciu \(x_d(\alpha) = \frac{v_0^2}{g}\sin2\alpha\) bez diferenciálneho počtu len využitím symetrie paraboly. Vrchol paraboly sa nachádza v strede medzi nulovými bodmi. Preto možno \(x\)-súradnicu bodu dopadu zapísať ako \(x_d(\alpha) = 2\cdot x_{max}\). To nám umožňuje vyhnúť sa riešeniu kvadratickej rovnice v súčinovom tvare získanej dosadením \(y=0\) do funkcie \(y(x)\).
Literatúra
- Kubera, Miroslav; Nečas, Tomáš; Beneš, Vojtěch. Online učebnice fyziky pro gymnázia - Vrhy [online]. Available from https://e-manuel.cz/kapitoly/pouziti-pohybovych-zakonu/vyklad/vrhy/ [cit. 27.9.2023].
- Moc, Ondřej; Eisenmann, Petr. Šikmý vrh z rozhledny [online]. Available from https://mfi.upol.cz/files/26/2602/mfi_2602_129_137.pdf [cit. 27.9.2023]