Strzał piłką golfową
 30 min.,
30 min.,  3/3
3/3 Skośny ruch pocisku
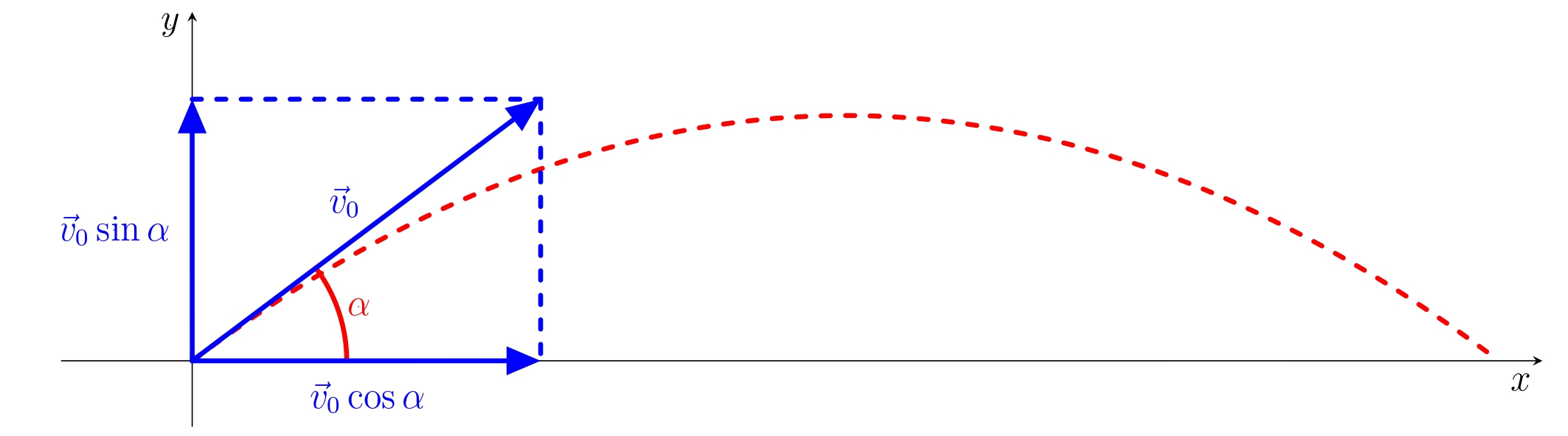
Ruch pocisku jest najbardziej ogólnym sposobem wprawiania w ruch obiektu znajdującego się w jednorodnym polu grawitacyjnym. Załóżmy, że ciało (masa punktowa) jest wyrzucane ukośnie w przestrzeń bez oporu. Prędkość początkowa wynosi \(\vec{v}_0\), a kąt pomiędzy wektorem \(\vec{v}_0\) i kierunkiem poziomym wynosi $. Wprowadźmy kartezjański układ współrzędnych z poziomą osią \(x\) i pionową osią \(y\), jak pokazano na rysunku. Współrzędne wektora prędkości początkowej są następujące \[\vec{v}_0=(v_0\cos\alpha,v_0\sin\alpha).\]
Ruch ciała jest regulowany przez przyspieszenie grawitacyjne \(g\) skierowane pionowo w dół. Pozioma składowa przyspieszenia grawitacyjnego wynosi zero, dlatego ruch w kierunku poziomym pozostaje bez wpływu pola grawitacyjnego. Pionowa składowa ruchu jest pod wpływem ujemnego przyspieszenia \(-g\). Stąd jest to ruch ze stałym (równomiernym) opóźnieniem i prędkością początkową \(v_0t\sin\alpha\).
Możemy użyć wzorów na odległość ruchu ze stałą prędkością i stałym przyspieszeniu do ilościowego określenia współrzędnych punktu masy. W ten sposób otrzymujemy
\[ \begin{aligned} x(t) &= v_0 t\cos\alpha,\\ y(t) &= v_0t\sin\alpha-\frac{1}{2}gt^2. \end{aligned}\tag{1} \]
Ruch piłki golfowej
Golfista uderza piłkę z prędkością początkową \(v_0\). Kąt między prędkością początkową a płaszczyzną poziomą wynosi \(\alpha\) . Załóżmy, że siła oporu jest pomijalna. Ruch kuli spełnia warunki ruchu pocisku wystrzelonego pod kątem w środowisku bez oporu powietrza.
Ćwiczenie 1. Udowodnij, że trajektoria piłki golfowej podąża ścieżką paraboliczną.
Rozwiązanie: Znajdz równanie trajektorii w postaci \(y=f(x)\) . Konieczne jest wyeliminowanie parametru \(t\) z układu (1).
Rozwiązujemy pierwsze równanie względem czasu \(t=\frac{x}{v_0\cos\alpha}\) i podstawiamz do drugiego równania: \[y(x) = v_0\sin\alpha\,\frac{x}{v_0\cos\alpha} -\frac{1}{2}g\frac{x^2}{v_0^2\cos^2\alpha}= -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .\] Stąd widzimy, że współrzędna \(y\) trajektorii jest funkcją kwadratową współrzędnej \(x\), a trajektoria piłki golfowej jest zatem opisana przez parabolę.
Ćwiczenie 2. Oblicz wysokość rzutu, tj. maksymalną wysokość piłki golfowej. wysokość \(y_{max}\) jaką osiągnie wystrzelona kula.
Rozwiązanie: Wysokość rzutu (ruch pocisku) to maksimum funkcji z poprzedniego ćwiczenia: \[f\colon y = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .\]
Pochodną funkcji \(f\) obliczamy jako
\[ y'=-\frac{g}{2v_0^2\cos^2\alpha}\cdot2x+\frac{\sin\alpha}{\cos\alpha}\ . \]
Aby znaleźć punkt stacjonarny, ustawiamy pochodną równą zero i otrzymujemz równanie
\[ \frac{g}{v_0^2\cos^2\alpha}\cdot x=\frac{\sin\alpha}{\cos\alpha}\ . \]
Rozwiązaniem tego równania jest
\[ x_{max}=\frac{v_0^2\sin\alpha\cos\alpha}{g}\ . \]
Ponieważ trajektoria ruchu jest wklęsłą funkcją kwadratową, zlokalizowany punkt stacjonarny jest maksimum, a współrzędna pionowa tego punktu jest wysokością rzutu.
Wysokość rzutu oblicza się poprzez obliczenie funkcji \(f\) w uzyskanej współrzędnej \(x_{max}\):
\[y_{max}=\frac{v_0^2\sin^2\alpha}{2g}\ .\]
Ćwiczenie 3. Biorąc pod uwagę stałą prędkość początkową, znajdź kąt \(\alpha\) który gwarantuje maksymalną odległość między punktem początkowym a punktem końcowym trajektorii.
Rozwiązanie Aby znaleźć maksymalny kąt zasięgu, musimy uzyskać punkt końcowy \(x_d\) trajektorii jako funkcję kąta
\(\alpha\) i znaleźć maksimum funkcji \(x_d(\alpha)\) Biorąc pod uwagę że \(y=0\), gdy piłka uderza w ziemię, znajdujemy zero funkcji
\[y(x) = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x.\]
Stąd otrzymujemy:
\[0 = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ ,\]
\[0 = x\cdot\left(-\frac{g}{2v_0^2\cos^2\alpha}\cdot x+\frac{\sin\alpha}{\cos\alpha}\right)\ .\]
To równanie ma dwa rozwiązania. Pierwsze rozwiązanie \(x=0\) odpowiada miejscu wystrzelenia piłki, a drugie rozwiązanie \(x_d\) do miejsca uderzenia
\[ x_d(\alpha) = \frac{2v_0^2\sin\alpha\cos\alpha}{g}=\frac{v_0^2}{g}\sin2\alpha\ . \]
Teraz musimy znaleźć maksimum funkcji \(x_d(\alpha)\). Wystarczy znaleźć punkt stacjonarny, ponieważ wykazano, że trajektoria jest parabolą, która otwiera się w dół. Obliczamy pochodną funkcji \(x_d(\alpha)\) względem \(\alpha\)
\[ x_d'(\alpha)=\frac{v_0^2}{g}\cdot\cos2\alpha\cdot 2\ . \]
Ustawiając pochodną równą zero, otrzymujemy \(\cos2\alpha=0\), który jest spełniony dla \(2\alpha=90^\circ\) ( piłka zostanie wystrzelona, oczywiście \(\alpha\in\langle0^\circ,90^\circ\rangle\), więc rozwiązanie jest jednoznaczne). Tak więc punkt stacjonarny to \(\alpha=45^\circ\).
Maksymalny zasięg w golfie osiąga się uderzając piłkę pod kątem \(\alpha=45^\circ\) a piłka ląduje w odległości
\[ x_d(45^\circ) =\frac{v_0^2}{g}\sin(2\cdot45^\circ)=\frac{v_0^2}{g}. \]
Należy zauważyć, że możliwe jest uzyskanie funkcji \(x_d(\alpha) = \frac{v_0^2}{g}\sin2\alpha\) bez rachunku różniczkowego, wykorzystując symetrię paraboli. Wierzchołek paraboli znajduje się w środku punktów zerowych. Dlatego współrzędna $x punktu uderzenia można określić ilościowo jako \(x_d(\alpha) = 2\cdot x_{max}\).
Pozwala nam to uniknąć rozwiązywania równania kwadratowego otrzymanego przez podstawienie \(y=0\) do funkcji \(y(x)\) i faktoryzując prawą stronę.
Literatura
- Kubera, Miroslav; Nečas, Tomáš; Beneš, Vojtěch. Podręcznik online fizyka dla szkół średnich - Linie [online]. Dostępne pod adresem https://e-manuel.cz/kapitoly/pouziti-pohybovych-zakonu/vyklad/vrhy/. [cytowany 2023 września 27].
- Moc, Ondřej; Eisenmann, Petr. Pochyły szczyt z wieży. [online]. Dostępne pod adresem https://mfi.upol.cz/files/26/2602/mfi_2602_129_137.pdf [cytowany 27.9.2023]