Odpal golfového míčku
 30 min.,
30 min.,  3/3
3/3 Šikmý vrh
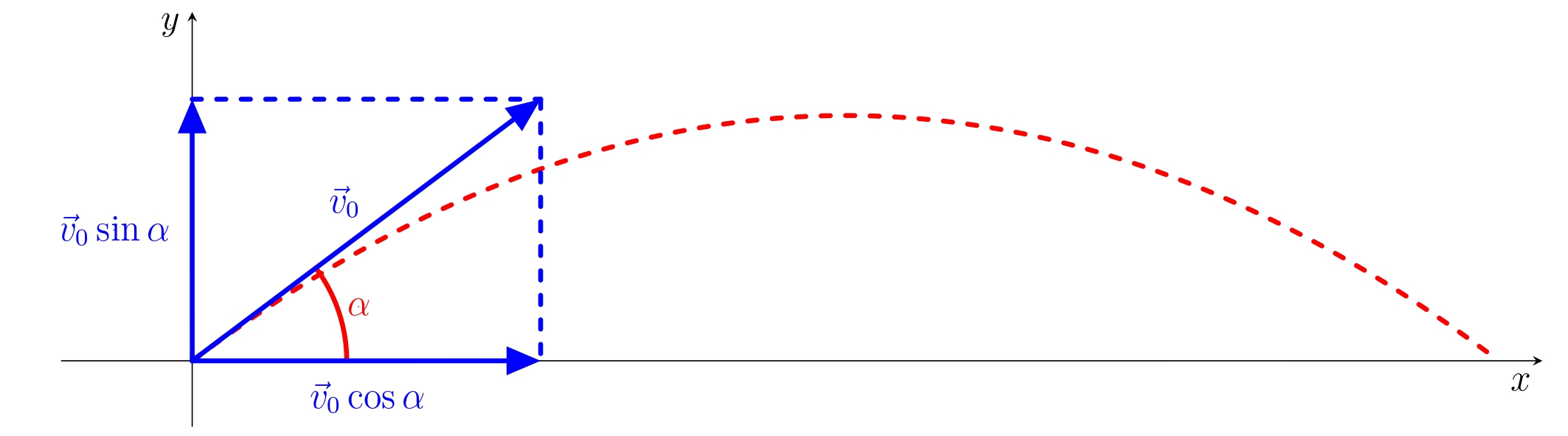
Šikmý vrh je nejobecnější způsob uvedení tělesa v homogenním tíhovém poli do pohybu. Předpokládejme, že hmotný bod byl šikmo vržen v prostředí bez odporu a vektor jeho počáteční rychlosti \(\vec {v}_0\) svírá s vodorovnou rovinou úhel \(\alpha\). Při zavedení kartézského souřadného systému s osou \(x\) vodorovnou ve směru vrhu a osou \(y\) svislou vzhůru bude počáteční rychlost dána vektorem
\[\vec{v}_0=(v_0\cos\alpha,v_0\sin\alpha).\]
Pohyb tělesa je ovlivněn tíhovým zrychlením o velikosti \(g\) mířícím svisle dolů. Vodorovná komponenta tíhového zrychlení je nulová a proto ve vodorovném směru pohyb není tíhovým polem ovlivněn. Ve směru svislém je pohyb tělesa ovlivněn zrychlením \(-g\) a jedná se o rovnoměrně zpomalený pohyb s počáteční rychlostí \(v_0\sin\alpha\).
Pro souřadnice polohy hmotného bodu bude platit
\[ \begin{aligned} x(t) &= v_0 t\cos\alpha,\\ y(t) &= v_0t\sin\alpha-\frac{1}{2}gt^2. \end{aligned}\tag{1} \]
Odpal golfového míčku
Hráč golfu odpaluje míček počáteční rychlostí \(v_0\) svírající s vodorovnou rovinou úhel \(\alpha\). Předpokládejme, že na míček působí zanedbatelné odporové síly. Pohyb míčku tedy splňuje podmínky pro pohyb šikmo vrženého tělesa v prostředí bez odporu vzduchu.
Úloha 1. Dokažte, že trajektorií golfového míčku je parabola.
Řešení. Pro nalezení rovnice trajektorie, tedy funkce \(y=f(x)\), je nutné z rovnic (1) určujících polohu bodu odstranit parametr \(t\).
Proto vyjádříme z první rovnice čas \(t=\frac{x}{v_0\cos\alpha}\) a dosadíme ho do rovnice druhé: \[y(x) = v_0\sin\alpha\,\frac{x}{v_0\cos\alpha} -\frac{1}{2}g\frac{x^2}{v_0^2\cos^2\alpha}= -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .\] Odtud vidíme, že \(y\)-ová souřadnice trajektorie je kvadratickou funkcí \(x\)-ové souřadnice a trajektorií golfového míčku je proto parabola.
Úloha 2. Vypočítejte výšku vrhu, tj. maximální výšku \(y_{max}\), do které se dostane vystřelený míček.
Řešení. Pro výpočet výšky vrhu potřebujeme vypočítat extrém funkce z předchozího bodu: \[f\colon y = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .\] Vypočítáme derivaci funkce \(f\)
\[ y'=-\frac{g}{2v_0^2\cos^2\alpha}\cdot2x+\frac{\sin\alpha}{\cos\alpha}\ . \] Pro nalezení stacionárního bodu položíme derivaci rovnu nule a dostaneme rovnici \[ \frac{g}{v_0^2\cos^2\alpha}\cdot x=\frac{\sin\alpha}{\cos\alpha}\ . \] Jejím řešením je \[ x_{max}=\frac{v_0^2\sin\alpha\cos\alpha}{g}\ . \] Vzhledem k tomu, že trajektorií pohybu je konkávní kvadratická funkce, musí být nalezený stacionární bod jejím maximem, tj. jeho svislá souřadnice odpovídá výšce vrhu.
Výšku vrhu vypočítáme dosazením získané souřadnice \(x_{max}\) do funkce \(f\): \[y_{max}=\frac{v_0^2\sin^2\alpha}{2g}\ .\]
Úloha 3. Vypočítejte, při jakém úhlu \(\alpha\) doletí míček při konstantní velikosti počáteční rychlosti do maximální vzdálenosti.
Řešení. Pro výpočet úhlu maximálního dostřelu potřebujeme získat souřadnice \(x_d\) místa dopadu jako funkci úhlu \(\alpha\) a tuto funkci maximalizovat, tj. najdeme maximum funkce \(x_d(\alpha).\) Vzhledem k tomu, že při dopadu míčku bude \(y=0\), dosadíme do funkce \[y(x) = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\] za \(y\) nulovou výšku a vyřešíme získanou rovnici: \[0 = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ ,\] \[0 = x\cdot\left(-\frac{g}{2v_0^2\cos^2\alpha}\cdot x+\frac{\sin\alpha}{\cos\alpha}\right)\ .\] Tato rovnice v součinovém tvaru má dvě řešení. První řešení \(x=0\) odpovídá místu odpalu míčku a druhé řešení \(x_d\) místu dopadu \[ x_d(\alpha) = \frac{2v_0^2\sin\alpha\cos\alpha}{g}=\frac{v_0^2}{g}\sin2\alpha\ . \] Nyní je nutné nalézt maximum funkce \(x_d(\alpha)\). Vzhledem k tvaru trajektorie stačí najít její stacionární bod. Vypočítáme derivaci funkce \(x_d(\alpha)\) podle \(\alpha\)
\[ x_d'(\alpha)=\frac{v_0^2}{g}\cdot\cos2\alpha\cdot 2\ . \]
Položíme-li derivaci rovnu nule, dostaneme pro stacionární bod \(\cos2\alpha=0\), což je splněno pro \(2\alpha=90^\circ\) (pro odpal míčku zřejmě platí \(\alpha\in\langle0^\circ,90^\circ\rangle\), proto je řešení jednoznačné). Odsud \(\alpha=45^\circ\).
Maximálního dostřelu při golfu docílíme při odpalu pod úhlem \(\alpha=45^\circ\) a míček dopadne do vzdálenosti \[ x_d(45^\circ) =\frac{v_0^2}{g}\sin(2\cdot45^\circ)=\frac{v_0^2}{g}\ .\]
Funkci \(x_d(\alpha) = \frac{v_0^2}{g}\sin2\alpha\) jsme mohli získat i snadněji využitím symetrie paraboly. Vrchol paraboly totiž leží uprostřed trajektorie míčku. Proto pro místo dopadu \(x_{d}\) platí \(x_d(\alpha) = 2\cdot x_{max}\). Tím se vyhneme řešení kvadratické rovnice v součinovém tvaru získané dosazením \(y=0\) do funkce \(y(x)\).
Literatura
- Kubera, Miroslav; Nečas, Tomáš; Beneš, Vojtěch. Online učebnice fyziky pro gymnázia - Vrhy [online]. Dostupné z https://e-manuel.cz/kapitoly/pouziti-pohybovych-zakonu/vyklad/vrhy/ [cit. 27.9.2023].
- Moc, Ondřej; Eisenmann, Petr. Šikmý vrh z rozhledny [online]. Dostupné z https://mfi.upol.cz/files/26/2602/mfi_2602_129_137.pdf [cit. 27.9.2023]