Cruzando el río
 25 min.,
25 min.,  1/3
1/3 El barquero debe llegar desde su embarcadero en una orilla del río hasta el otro muelle, que se encuentra en la orilla opuesta, \(500\ \text{m}\) río abajo. El río entre los muelles es recto y \(100\ \text{m}\) de ancho. La velocidad de la corriente es de \(2\ \text{m}/\text{s}\). También sabemos que la barca del barquero se mueve a una velocidad de \(12\ \text{km}/\text{h}\) respecto al agua.
Problema 1. El barquero quiere viajar directamente de un muelle al otro. Él puede lograr esto inclinando el barco a través del río y manteniendo esta dirección. ¿Con qué ángulo debe el barquero desviarse de la trayectoria directa para llegar directamente al otro muelle?
Solución. Denotemos por \(A\) y \(B\) el punto de partida y de llegada. Denotemos también por \(P\) el pie de la recta perpendicular desde el punto \(B\) hasta la orilla opuesta del río. A continuación, marquemos los vectores de la velocidad de la corriente, la velocidad de la embarcación respecto al agua y la velocidad resultante de la embarcación (velocidad de la embarcación respecto al fondo del río) todos ellos con sus puntos iniciales en el punto A y sus puntos finales de la siguiente forma (ver figura):
- \(\overrightarrow{AM}\) es el vector de la velocidad de la corriente.
- \(\overrightarrow{AL}\) es el vector de la velocidad del barco con respecto al agua (sin incluir la corriente).
- \(\overrightarrow{AK}\) es el vector de la velocidad resultante de la embarcación respecto al fondo del río (corriente + velocidad de la embarcación).
Como \(K\in AB\), nuestra tarea es determinar el ángulo \(KAL\), que denotamos por \(\alpha\). Por la regla de adición de vectores, el cuadrilátero \(MALK\) es un paralelogramo.
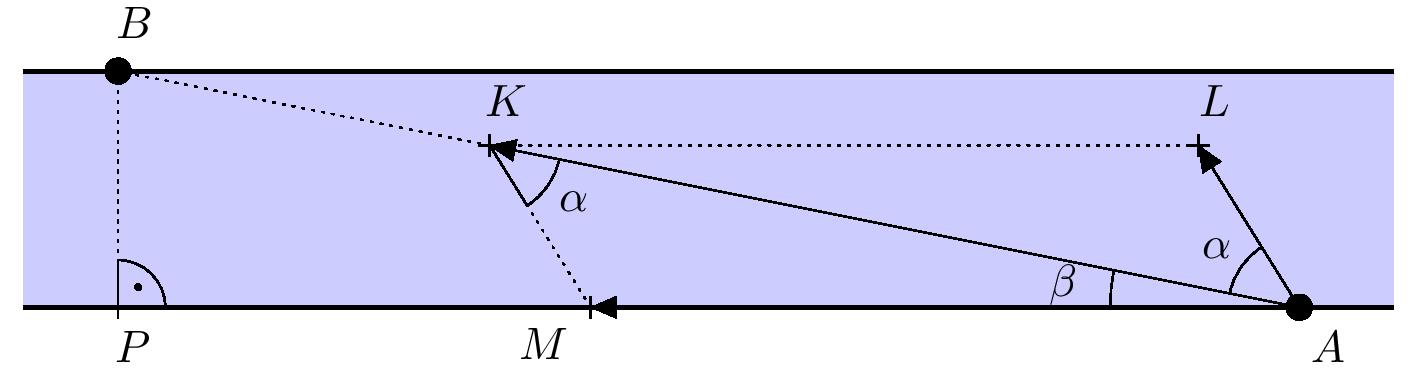
Además, vamos a denotar \(\lvert \sphericalangle MAK \rvert = \beta\). Entonces \(\lvert \sphericalangle MAL \rvert = \alpha + \beta\). Se da que \(|BP|=100\ \text{m}\) y \(|AP|=500\ \text{m}\). Utilizando la función tangente en el triángulo rectángulo \(PAB\) obtenemos \(\beta = \arctan\frac{1}{5} \doteq 11^{\circ}19'\).
Como un paralelogramo se divide por su diagonal en dos triángulos congruentes, se cumple que \(\lvert \sphericalangle AKM \rvert= \lvert \sphericalangle KAL \rvert = \alpha\). Para calcular \(\alpha\), utilizamos la ley de los senos para el triángulo \(AKM\). Tras convertir las longitudes de los lados a una unidad común (km/h en nuestra solución), obtenemos concretamente \(|KM|=12\,\text{km/h}\) y \(|AM|=2\cdot 3.6=7.2\,\text{km/h}\). Expresamos ahora \(\alpha\) a partir de la ley de los senos:
\[ \frac{|KM|}{\sin \beta} = \frac{|AM|}{\sin \alpha} \] \[ \sin \alpha = \frac{|AM|}{|KM|}\cdot \sin\beta \qquad \Rightarrow \qquad \alpha = \arcsin \left( \frac{|AM|}{|KM|}\cdot \sin\beta \right) \] Tras sustituir los valores, obtenemos \(\alpha \doteq 6^{\circ}45'\). Así, el barquero tiene que girar su barco aproximadamente 7^{circ}$ a la derecha desde el rumbo directo al destino.
Problema 2. Si el reloj digital del barco marca las 11:00 en el momento de la salida (sin mostrar los segundos), ¿qué hora marcará el reloj en el momento en que el barco llegue al otro muelle?
Solución. Determinemos primero la distancia entre los dos muelles utilizando el teorema de Pitágoras en el triángulo rectángulo \(ABP\):
\[ \begin{aligned} |AB| &= \sqrt{|AP|^2 + |BP|^2}\\ |AB| &= \sqrt{0.5^2 + 0.1^2}\,\text{km}\\ |AB| &\doteq 0.51\,\text{km}. \end{aligned} \]
Ahora determinamos la magnitud de la velocidad resultante de la barca respecto al fondo del río, que es igual a la longitud del segmento de recta \(AK\). Esto, por ejemplo, se puede determinar utilizando la ley de los cosenos en el triángulo \(AKM\). Denotamos el ángulo interior \(\lvert \sphericalangle AMK \rvert =\gamma\), que mide \(180^{\circ}-\alpha - \beta \doteq 161^{\circ}56'\). Entonces para \(|AK|\) podemos escribir:
\[ \begin{aligned} |AK| &= \sqrt{|KM|^2 + |AM|^2 - 2\cdot |KM| \cdot |AM| \cdot \cos \gamma}\\ |AK| &= \sqrt{12^2 + 2^2 - 2\cdot 12 \cdot 2 \cdot \cos(161^{\circ}56')}\,\text{km/h}\\ |AK| &\doteq 19.0\,\text{km/h} \end{aligned} \] El barco recorre un trayecto directo de \(0.51\ \text{km}\) a una velocidad media de \(19\ \text{km}/\text{h}\), lo que tarda: \[ \begin{aligned} t &= \frac{\text{espacio recorrido}}{\text{velocidad}}\\ t &= \frac{0.51}{19}\ \text{h}\\ \end{aligned} \]
que son aproximadamente 97 segundos. Por lo tanto, el reloj mostrará las 11:01 o las 11:02 al llegar al muelle de destino.