Přeplutí řeky
 25 min.,
25 min.,  1/3
1/3 Převozník se musí dostat ze svého přístaviště na břehu řeky do druhého přístaviště, které se nachází na opačném břehu \(500\ \text{m}\) po proudu. Na tomto úseku řeka nemá žádné zákruty, teče rychlostí \(2\ \text{m}/\text{s}\) a je široká \(100\ \text{m}\). Dále víme, že převozníkova loď pluje vůči vodě rychlostí \(12\ \text{km}/\text{h}\).
Úloha 1. O kolik stupňů by měl převozník stočit svou loď vůči přímému směru k cíli?
Řešení. Označme výchozí přístaviště \(A\) a cílové přístaviště \(B\) a dále označme \(P\) patu kolmice spuštěné z bodu \(B\) na protější břeh řeky. Dále vyznačme vektory rychlosti řeky, rychlosti lodi vůči vodě a celkové rychlosti lodi na vodě do počátečního bodu \(A\):
- \(\overrightarrow{AM}\) je vektor rychlosti proudu řeky;
- \(\overrightarrow{AL}\) je vektor rychlosti lodi vůči vodě (bez započtení proudu);
- \(\overrightarrow{AK}\) je vektor výsledné rychlosti vůči zemskému povrchu (proud + rychlost vody).
Přičemž platí, že \(K\in AB\) a dle pravidla pro sčítání vektorů je čtyřúhelník \(MALK\) rovnoběžník. Naším úkolem je určit velikost úhlu \(KAL\), kterou označíme \(\alpha\).
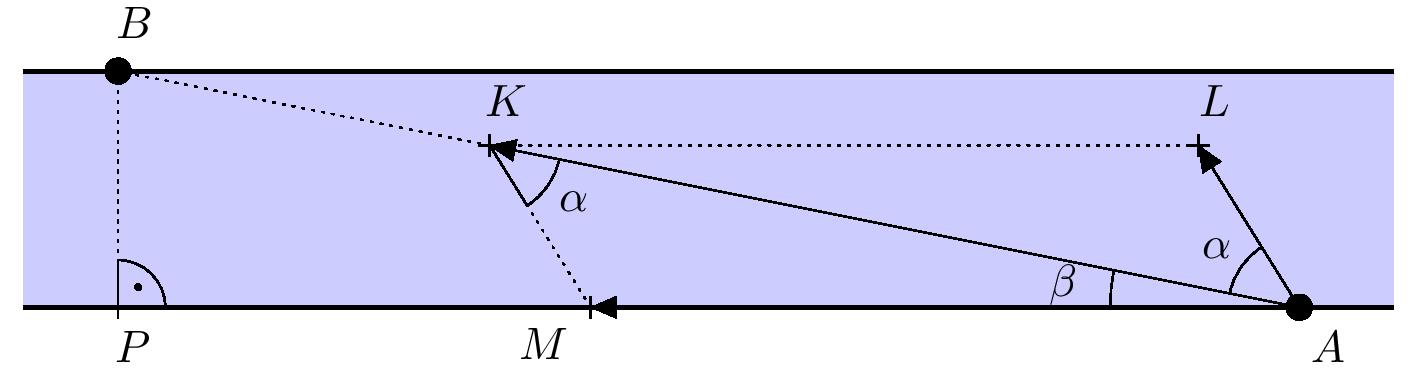
Označme \(\lvert \sphericalangle MAK \rvert = \beta\), tedy platí \(\lvert \sphericalangle MAL \rvert = \alpha + \beta\). Ze zadání víme, že \(|BP|=100\ \text{m}\) a \(|AP|=500\ \text{m}\); užitím funkce tangens v pravoúhlém trojúhelníku \(PAB\) tak dostáváme \(\beta = \arctg\,\frac{1}{5}\doteq 11^{\circ}19'\).
Protože je rovnoběžník půlen svou úhlopříčkou na dva shodné trojúhelníky, je \(\lvert \sphericalangle AKM \rvert= \lvert \sphericalangle KAL \rvert = \alpha\). K výpočtu \(\alpha\) využijeme sinovou větu pro trojúhelník \(AKM\), neboť velikosti \(|KM|\) a \(|AM|\) jeho stran odpovídají skutečným velikostem zadaných rychlostí. Po převodu na společnou jednotku (v našem řešení km/h) dostáváme konkrétně \(|KM|=12\,\text{km/h}\) a \(|AM|=2\cdot 3{,}6=7{,}2\,\text{km/h}\). Vyjádřeme nyní ze sinové věty:
\[ \frac{|KM|}{\sin \beta} = \frac{|AM|}{\sin \alpha} \] \[ \sin \alpha = \frac{|AM|}{|KM|}\cdot \sin\beta \qquad \Rightarrow \qquad \alpha = \arcsin \left( \frac{|AM|}{|KM|}\cdot \sin\beta \right) \] Po dosazení konkrétních hodnot dostáváme \(\alpha \doteq 6^{\circ}45'\). Převozník tak musí stočit svou loď o přibližně \(7^{\circ}\) doprava oproti přímému směru k cíli.
Úloha 2. Jestliže digitální hodiny na lodi ukazují v okamžik vyplutí 11:00 (sekundy neukazují), kolik na nich bude v okamžiku, kdy loď přijede do druhého přístaviště?
Řešení. Určeme nejprve vzdálenost obou přístavišť užitím Pythagorovy věty v pravoúhlém trojúhelníku \(ABP\):
\[ \begin{aligned} |AB| &= \sqrt{|AP|^2 + |BP|^2}\\ |AB| &= \sqrt{0{,}5^2 + 0{,}1^2}\ \text{km}\\ |AB| &\doteq 0{,}51\,\text{km}. \end{aligned} \]
Nyní musíme určit velikost rychlosti lodi vzhledem k zemskému povrchu, která je rovna velikosti úsečky \(AK\). Tu můžeme určit např. z kosinové věty pro trojúhelník \(AKM\). Vnitřní úhel \(\gamma\) přilehlý vrcholu \(M\) má přitom velikost \(180^{\circ}-\alpha - \beta\).
\[ \begin{aligned} |AK| &= \sqrt{|KM|^2 + |AM|^2 - 2\cdot |KM| \cdot |AM| \cdot \cos \gamma}\\ |AK| &= \sqrt{12^2 + 2^2 - 2\cdot 12 \cdot 2 \cdot \cos(161^{\circ}56')}\,\text{km/h}\\ |AK| &\doteq 19{,}0\,\text{km/h}. \end{aligned} \] Loď tak urazí dráhu \(0{,}51\ \text{km}\) rychlostí \(19\ \text{km}/\text{h}\), což jí zabere čas \[ \begin{aligned} t &= \frac{\text{dráha}}{\text{rychlost}}\\ t &= \frac{0{,}51}{19}\ \text{h}\\ \end{aligned} \] tj. přibližně 97 sekund. V cíli tak budou hodiny ukazovat 11:01 nebo 11:02.