Precio Óptimo de la Entrada
 30 min.,
30 min.,  1/3
1/3 El propietario del carrusel quiere establecer el precio de la entrada para su atracción de forma que su beneficio sea máximo. Para simplificar, fija el precio de la entrada en múltiplos de 10 CZK. Sabe que, con el precio actual de 50 CZK, puede esperar unos 600 visitantes al día. Por su experiencia de años anteriores, estima que si el precio de la entrada aumenta 10 CZK, acudirán unos 50 visitantes menos al día. Al contrario, si el precio de la entrada disminuye 10 CZK, asistirán 50 visitantes más. Además, para fomentar el interés, uno de cada tres visitantes recibirá un algodón de azúcar por valor de 30 CZK a cargo del propietario.
Como resulta que el hijo del dueño está estudiando matemáticas, decide ayudar a su padre con este problema.
Ejercicio 1. Después de pensarlo un poco, el hijo escribió la fórmula
\[ y= (50+10x)\cdot (600-50x) - \frac{600-50x}{3}\cdot 30.\] Interpreta cada una de las partes de esta fórmula.
Solución. La siguiente tabla explica el significado de cada parte de la fórmula:
| Parte de la fórmula | Significado |
|---|---|
| \(10x\) | cambio en el precio de la entrada por \(x\cdot 10\ \text{CZK}\) |
| \(50+10x\) | nuevo precio de la entrada |
| \(600-50x\) | número estimado de visitantes depués del cambio de precio |
| \((50+10x)(600-50x)\) | ingresos por entradas diarias |
| \(\frac{600-50x}{3}\) | número de visitantes que reciben algodón de azúcar |
| \(\frac{600-50x}{3}\cdot 30\) | coste diario del algodón de azúcar |
| \(y\) | beneficio diario total |
Ejercicio 2. Si consideramos la anterior fórmula como una función de la variable \(x\), ¿qué tipo de función es y cómo es su gráfica?
Solución. Simplificando el lado derecho dela fórmula, la convertimos a la forma \[ y=-500x^2+4\ 000x+24\ 000\ . \] Esta es una función cuadrática cuya gráfica es una parábola. Debido al coeficiente negativo del término cuadrático, esta parábola es cóncava hacia abajo.
Ejercicio 3. ¿A qué precio de entrada se obtendría el máximo beneficio?
Solución. Nuestra tarea es determinar el máximo de la función \[f(x)=-500x^2+4\ 000x+24\ 000\ .\] Sabemos que la gráfica de la función \(f\) interseca con el eje \(x\) en los puntos correspondientes a las raíces del polinomio cuadrático. En el punto medio del segmento que une estos puntos, podemos encontrar el máximo de la función que estamos buscando (debido a la simetría de la parábola). Por lo tanto, determinamos las raíces del polinomio cuadrático. \[\begin{aligned} -500x^2 + 4\,000x + 24\,000 &= 0 \\ x^2 - 8x - 48 &= 0\\ (x-12)(x+4)&=0 \end{aligned}\] Las soluciones de la ecuación son las raíces \(x_1=12\) y \(x_2=-4\), luego el máximo de la función \(f\) es el punto \(x_{max}=\frac{12-4}{2}=4\). Por lo tanto, hemos aumentado el precio original de la entrada en \(40\) hasta el nuevo precio de \(90\ \text{CZK}\) para conseguir el máximo beneficio.
Exercise 4. ¿En cuánto es mayor el beneficio máximo que el beneficio con el precio original de la entrada?
Solución. La respuesta a este problema es la diferencia \(f(4)-f(0)\). Sustituyendo ambos valores en la función \(f\), obtenemos \(f(4)=32 000\) y \(f(0)=24 000\). La diferencia entre las dos cantidades es \(8 000\ \text{CZK}\). A continuación se muestra la gráfica de la función \(f\) con los valores \(f(4)\) y \(f(0)\) señalados:
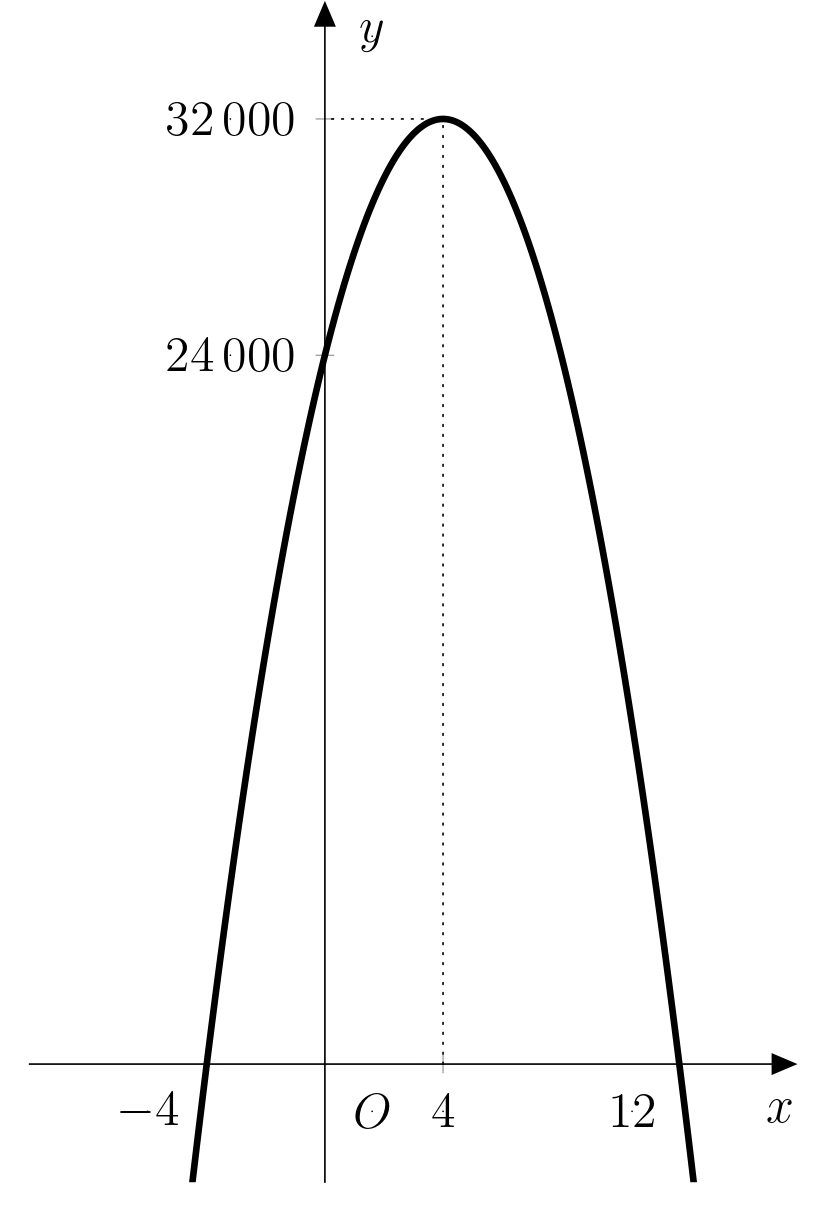
Ejercicio 5. Al crear la fórmula, el hijo simplificó un aspecto del problema. ¿Sabes cuál? ¿Podrías resolver el problema sin esta simplificación? Compara tu modelo con el del hijo del propietario del carrusel.
Solución. La fórmula del hijo es exacta solo si el número de visitantes al día \(600-50x\) es divisible por tres. En caso contrario, entonces el número de visitantes que reciben el regalo es la parte entera inferior del número \(\frac{600-50x}{3}\), denotada como \(\left\lfloor\frac{600-50x}{3}\right\rfloor\).
La función que toma como entrada un número real \(x\) y devuelve el mayor entero \(m\) tal que \(m\leq x\) se llama función de parte entera. Por ejemplo, \(\left\lfloor \frac{5}{2}\right\rfloor = 2\), \(\left\lfloor \pi\right\rfloor = 3\) nebo \(\left\lfloor -8{,}3\right\rfloor = -9\).
Ahora, vamos a comparar la función anteriormente usada \(f\) con la nueva función \(g\), la cual usa la parte entera inferior: \[ g(x) = (50+10x)\cdot (600-50x) - \left\lfloor\frac{600-50x}{3}\right\rfloor\cdot 30. \] \(x_{max}=4\). Compararemos los resultados alrededor del máximo ya determinado, \(x_{max}=4\). Para \(x\), sustituiremos valores del intervalo \(\langle 3{,}5;4{,}5 \rangle\), considerando valores para los que tanto el precio de la entrada como el número de visitantes sean enteros. Se puede observar que basta con que el precio de la entrada sea un entero, lo que ocurrirá para valores de \(x\) con un decimal como máximo.
Los valores de la función pueden resumirse en una tabla (es recomendable utilizar programas como MS Excel para los cálculos):
\[ \begin{array}{c|ccccccccccc} x & 3{,}5 & 3{,}6 & 3{,}7 & 3{,}8 & 3{,}9 & 4{,}0 & 4{,}1 & 4{,}2 & 4{,}3 & 4{,}4 & 4{,}5 \\\hline f(x) & 31\,875 & 31\,920 & 31\,955 & 31\,980 & 31\,995 & 32\,000 & 31\,995 & 31\,980 & 31\,955 & 31\,920 & 31\,875 \\\hline g(x) & 31\,895 & 31\,920 & 31\,965 & 32\,000 & 31\,995 & 32\,010 & 32\,015 & 31\,980 & 31\,965 & 31\,940 & 31\,875 \\ \end{array} \]
El beneficio diario determinado por la función \(g\) siempre es mayor o igual que el beneficio diario determinado por la función \(f\). Además, el máximo de la función \(g\) está en un punto diferente, en concreto \(4{,}1\), que corresponde al precio de entrada de \(91\ \text{CZK}\)
y una asistencia diaria de 395 personas.
Podemos observar los siguientes hechos:
Las diferencias entre los beneficios son muy pequeñas, simplemente fracciones del precio de una entrada individual. No importa si la entrada cuesta 90 o 91 CZK, porque la única persona que asiste de más (o no asiste) en comparación con las estimaciones, elimina totalmente cualquier diferencia entre los beneficios de los dos modelos.
Mientras el máximo de la función \(f\) se determina mediante un cálculo directo y relativamente sencillo, el máximo de la función \(g\) se calcula sustituyendo todos los valores admisibles (de un intervalo relativamente estrecho).
Por lo tanto, a pesar de la simplificación, utilizar la función \(f\) para calcular el beneficio máximo es suficiente y más conveniente.