Funkcje troficzne w modelach drapieżnik–ofiara

20 min., 1/3

Modele matematyczne odgrywają nieocenioną rolę w badaniach nad przyrodą. Modele te nie tylko pozwalają nam przewidywać przyszłe zmiany, ale służą również kilku innym ważnym celom.

Wykorzystanie modeli ekologicznych jest czasami określane jako stosowanie metod fizycznych w ekologii, ponieważ ekosystemy są badane pod kątem dynamiki populacji przy użyciu technik matematycznych opracowanych pierwotnie do rozwiązywania problemów fizycznych. Wyniki takich modeli mogą dostarczyć następujących informacji:

• Prognozowanie. Umiejętność pracy z matematycznymi modelami ekosystemów pozwala przewidywać przyszłe zmiany. Mogą one dotyczyć środowiska stabilnego lub takiego, w którym zmieniają się określone parametry. Zrozumienie modelu pozwala nam ocenić, jak takie zmiany wpłyną na ekosystem.
• Zrozumienie zasad. Modele matematyczne pomagają ekologom i naukowcom badać interakcje między różnymi elementami ekosystemów i uzyskać wgląd w ich dynamikę. To z kolei pomaga zidentyfikować czynniki, które kształtują strukturę i funkcjonowanie tych ekosystemów.
• Optymalizacja procesu podejmowania decyzji. Modelowanie matematyczne może być również wykorzystywane do usprawnienia procesu podejmowania decyzji w takich obszarach, jak ochrona różnorodności biologicznej lub zarządzanie lasami i rybołówstwem. Pomaga ono zidentyfikować najskuteczniejsze strategie osiągnięcia określonych celów.

Jedną z podstawowych relacji ekologicznych jest interakcja drapieżnik–ofiara. Relacja ta może być jedyną interakcją w danym ekosystemie lub może jej towarzyszyć kilka innych. Znaczenie modelowania współistnienia drapieżników i ofiar zostanie zilustrowane za pomocą kilku historycznie znaczących modeli.

Model Lotki-Volterry

W 1926 r. włoski matematyk Vito Volterra opublikował jeden z pierwszych modeli matematycznych interakcji drapieżnik–ofiara. Motywacją do tego była obserwacja dokonana podczas I wojny światowej, kiedy ograniczenia połowowe doprowadziły do wzrostu odsetka ryb drapieżnych w połowach. Na tę zaskakującą tendencję zwrócił uwagę Volterrze jego zięć, biolog morski Umberto D’Ancona, który spodziewał się czegoś przeciwnego: zakładał, że zmniejszenie presji połowowej spowoduje wzrost udziału mniejszych gatunków ryb, które służą jako ofiary dla drapieżników. Model Volterry wyjaśnił to zjawisko jako wynik prostych interakcji między rybami drapieżnymi a ich ofiarami.

Model składa się z dwóch równań. Pierwsze opisuje populację ofiar, zakładając, że rośnie ona naturalnie, ale wzrost ten jest ograniczony przez obecność drapieżników. Większa liczba drapieżników spowalnia wzrost populacji ofiar w bardziej znaczący sposób. Jeśli drapieżników jest zbyt wiele, populacja ofiar może nawet zacząć spadać i ostatecznie wyginąć. Drugie równanie opisuje populację drapieżników. Zakłada ono, że bez ofiar drapieżniki wymierają. Jednak im więcej jest ofiar, tym bardziej tendencja ta ulega odwróceniu, umożliwiając wzrost populacji drapieżników.

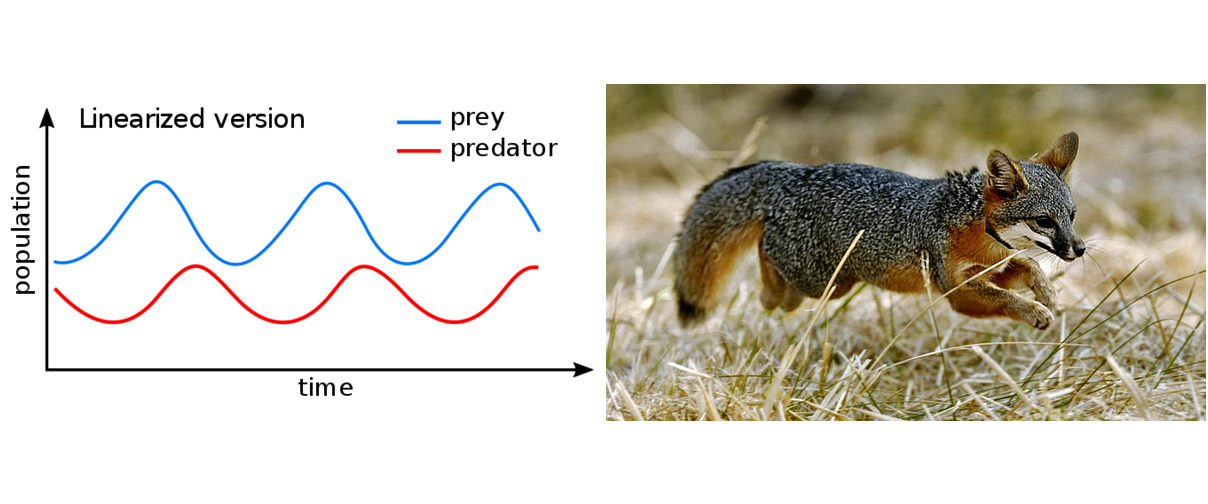
System ten w naturalny sposób tworzy cykle. Obfitość ofiar pozwala na wzrost populacji drapieżników. Wraz ze wzrostem liczby drapieżników wywierają one coraz większą presję na populację ofiar, ostatecznie doprowadzając do jej spadku. Prowadzi to do niedoboru pożywienia dla drapieżników, co z kolei powoduje spadek ich liczebności. W końcu populacja drapieżników staje się tak mała, że populacja ofiar odczuwa mniejszą presję i może ponownie wzrosnąć, ostatecznie osiągając swój pierwotny poziom. To z kolei pozwala populacji drapieżników na odbudowę, a cykl się powtarza. Te okresowe wahania liczebności populacji można wyraźnie zaobserwować w historycznych rejestrach handlu futrami z królików śnieżnych i rysiów w rejonie Zatoki Hudsona.

Model Volterry wyjaśniał nie tylko powstawanie takich cykli, ale także dlaczego ograniczenie polowań lub połowów może przesunąć punkt równowagi – wokół którego oscylują obie populacje – na korzyść drapieżnika, a nie ofiary. Zjawisko to, zaobserwowane przez D’Anconę, znane jest jako efekt Volterry.

Ten sam model został zaproponowany już wcześniej, w 1910 roku, przez amerykańskiego matematyka Alfreda J. Lotkę. Z tego powodu jest on obecnie znany jako model Lotki-Volterry.

Model pączkowca świerkowego

Podobne okresowe wahania, jak te opisane w modelu Lotki-Volterry, można również zaobserwować w lasach kanadyjskich. Mniej więcej co 30–40 lat dochodzi do masowego pojawienia się pączkowca świerkowego (Choristoneura fumiferana). Gatunek ten występuje zazwyczaj w stosunkowo niewielkiej liczbie, ale w niektórych latach jego populacja wzrasta tysiąckrotnie. Podczas takich epidemii larwy mogą zniszczyć nawet 80% drzew w lesie, skutecznie dewastując cały obszar. Jedna z ostatnich epidemii na dużą skalę rozpoczęła się w 2006 roku w Quebecu. Do 2019 roku dotknęła ona około 9,6 miliona hektarów lasów [^1] – obszar większy niż powierzchnia Węgier. [^1]: source at https://www.nrcan.gc.ca. W 1978 roku naukowcy D. Ludwig, D. D. Jones i C. S. Holling zaproponowali model, który nie tylko opisywał dynamikę populacji brudnicy świerkowej, ale także pomagał wyjaśnić mechanizmy stojące za tymi epidemiami. Kluczowym czynnikiem było drapieżnictwo – a konkretnie ptaki żywiące się larwami brudnicy. W naturalnym ekosystemie ptaki pomagały kontrolować populację brudnicy, ale tylko do pewnego momentu. Gdy las osiągnął wystarczającą wielkość, zapewniał również obfite pożywienie dla budwormów. Ich populacja wzrosła wtedy tak bardzo, że ptaki osiągnęły nasycenie i nie były już w stanie konsumować larw w tempie wystarczającym do ograniczenia ich liczebności. W rezultacie rola ptaków jako drapieżników zmniejszyła się, a populacja budwormów gwałtownie wzrosła, powodując ostatecznie rozległe szkody w lesie.

W tym przypadku drapieżnictwo odgrywa kluczową rolę w ograniczaniu populacji budwormów. Jednak ponieważ ptaki rozmnażają się znacznie wolniej niż budwormy, ich populację można uznać za stałą dla celów modelowania. Gdy ptaki osiągną punkt nasycenia, mogą ograniczyć wzrost populacji budwormów tylko w ograniczonym zakresie. Po przekroczeniu pewnego progu kontrola ta staje się nieskuteczna, co prowadzi do niekontrolowanego wzrostu populacji i pełnej epidemii.

Model lisów wyspowych

Lis wyspowy (Urocyon littoralis) to wyjątkowy gatunek, endemiczny ssak żyjący wyłącznie na kilku małych wyspach u wybrzeży Kalifornii. Lis wyspowy, wielkością zbliżony do kota domowego, jest niezwykle ufny ze względu na brak naturalnych drapieżników w swoim środowisku. Jako gatunek jest bardzo wrażliwy i podatny na zagrożenia, charakteryzuje się niską zmiennością genetyczną i ograniczoną odpornością na choroby przenoszone z kontynentu. Jest jednym z najmniejszych psowatych na świecie i w przeciwieństwie do większości innych przedstawicieli rodziny psowatych potrafi wspinać się na drzewa.

W wyniku działalności człowieka populacja lisów wyspowych drastycznie spadła na przełomie tysiącleci. Na wyspie San Miguel liczba dorosłych osobników spadła z 450 w 1994 r. do zaledwie 15 w 1999 r.¹. Podobna sytuacja miała miejsce na okolicznych wyspach, z których każda jest domem dla własnego podgatunku lisa wyspowego. Spadek ten był spowodowany łańcuchem wydarzeń: produkcja środka owadobójczego DDT w latach 40. XX wieku doprowadziła do wyginięcia bielików amerykańskich (Haliaeetus leucocephalus) na tym obszarze. W związku z ich brakiem pojawiły się orły przednie (Aquila chrysaetos). W przeciwieństwie do bielików, które żywią się rybami, orły przednie preferują ssaki, co okazało się katastrofalne dla lisów wyspowych. Lis, niegdyś największy drapieżnik na wyspach, nagle stał się ofiarą – i na początku XXI wieku gatunek ten znalazł się na skraju wyginięcia. W przeciwieństwie do modelu Lotki-Volterry, nie było nadziei, że populacja lisów naturalnie się odbuduje dzięki oscylacjom drapieżnik-ofiara, ponieważ orły miały alternatywne źródła pożywienia, takie jak dziki i skunksy.

Na szczęście lis wyspowy został uratowany dzięki niezwykłym wysiłkom konserwatorskim. Po prawidłowym zidentyfikowaniu przyczyn spadku liczebności populacji można było rozpocząć działania mające na celu jej odbudowę. Konserwatorzy skupili się na zwiększeniu populacji lisów i stabilizacji ich środowiska. Obejmowało to eliminację dzikich świń, przeniesienie orłów przednich, ponowne wprowadzenie bielików amerykańskich, hodowlę lisów w niewoli, wypuszczanie ich na wolność oraz szczepienia przeciwko wprowadzonym chorobom. Wszystko to osiągnięto w rekordowym czasie – w ciągu zaledwie jednej dekady. Stało się to jednym z najbardziej udanych programów odbudowy populacji ssaków w historii.

Funkcje troficzne

Istotnym elementem modeli drapieżnik–ofiara – niezależnie od tego, który z powyższych przykładów weźmiemy pod uwagę – jest funkcja troficzna. Funkcja ta opisuje wpływ pojedynczego drapieżnika na populację ofiar. Wyraża ona tempo, w jakim jeden drapieżnik spowalnia wzrost populacji ofiar. Jeśli oznaczamy \(x\) jako wielkość populacji ofiar, a \(y\) jako tempo, w jakim jeden drapieżnik spowalnia wzrost populacji ofiar (tj. ilość ofiar złapanych przez jednego drapieżnika w jednostce czasu), to zależność tę można zapisać matematycznie jako: \[y=f(x).\] Spróbujemy zidentyfikować kilka naturalnych założeń, które powinna spełniać każda funkcja troficzna. Następnie spróbujemy znaleźć odpowiednią ogólną postać takiej funkcji.

Rozwiązanie.

1. Funkcja \(y=f(x)\) jest rosnąca.

2. Funkcja \(y=f(x)\) przechodzi przez punkt początkowy, tj. \(f(0)=0\).

3. Funkcja \(y=f(x)\) jest ograniczona od góry. Ponieważ funkcja jest rosnąca i jest ograniczona od góry, jej wykres ma asymptotę poziomą, gdy \(x\) dąży do nieskończoności.

Funkcja troficzna typu II Hollinga

Funkcja troficzna wyraża, ile ofiar pojedynczy drapieżnik konsumuje w jednostce czasu, biorąc pod uwagę wielkość populacji ofiar. Dlatego funkcja ta musi być zdefiniowana wyłącznie dla wartości nieujemnych, a jej wyniki również muszą być nieujemne (wynika to z punktów 1 i 2 poprzedniego ćwiczenia). W poprzedniej sekcji ustaliliśmy, że funkcja troficzna powinna przechodzić przez punkt początkowy i rosnąć w kierunku asymptoty poziomej — oznacza to, że funkcja powinna rosnąć, ale być ograniczona od góry. Właściwości te nie mogą być spełnione przez funkcję liniową, dlatego przechodzimy do najprostszego przypadku nieliniowego: odwrotnej proporcjonalności.

Rozwiązanie.

1. Funkcja uzyskana poprzez pionowe skalowanie \(y=\frac{1}{x}\) o współczynnik \(k\) jest następująca: \[y=\frac{k}{x}.\]

2. Odwrócenie uzyskuje się poprzez pomnożenie funkcji przez współczynnik \(-1\), a przesunięcie poprzez dodanie wartości \(S\). Te poprawki dają funkcję \[y=S-\frac{k}{x}.\]

3. Przesunięcie w lewo o \(b\) uzyskuje się poprzez zastąpienie wyrażenia \(x+b\) za \(x\). Daje nam to funkcję \[y=S-\frac{k}{x+b}.\] Po przeliczeniu na wspólny mianownik funkcja przyjmuje postać \[y=\frac{Sx+Sb}{x+b}-\frac{k}{x+b}=\frac{Sx + (Sb-k)}{x+b}.\] Aby zapewnić, że \(f(0)=0\), musimy mieć: \[Sb-k=0\]. Warunek ten pokazuje, że trzy stałe nie są niezależne, ale istnieje między nimi zależność.

Uwaga. W poprzednim ćwiczeniu wyprowadziliśmy ogólną postać jednej z podstawowych funkcji troficznych. Jest to funkcja rosnąca, która zaczyna się w punkcie początkowym i stopniowo rośnie w kierunku asymptoty poziomej. Tempo wzrostu spada wraz z upływem czasu. Taka funkcja nazywana jest funkcją Hollinga typu II. Zazwyczaj zapisuje się ją w postaci: \[f(x)=\frac {Sx}{x+b} (1),\tag{1}\] gdzie \(S\) jest poziomem nasycenia, a \(b\) jest stałą, której znaczenie zostanie wyjaśnione w następnym ćwiczeniu.

Rozwiązanie. Podstawiając bezpośrednio \(x=b\) do (1), otrzymujemy \[f(b)=\frac{Sb}{b+b}=\frac {Sb}{2b}=\frac S2.\] To dowodzi twierdzenia.

Poniższe ćwiczenie ilustruje proces odwrotny, w którym z funkcji troficznej w postaci (1) wyprowadzimy postać, która pokazuje, jak można ją uzyskać poprzez kolejne przekształcenia funkcji \(y=\frac {1}{x}\).

Rozwiązanie. Aby rozwiązać to zadanie, sprytnie przepisujemy ułamek. W liczniku tworzymy wielokrotność mianownika, dzielimy wyrażenie na dwa ułamki i upraszczamy:

\[\frac {6x}{x+2} = \frac {6(x+2)-12}{x+2}=\frac {6(x+2)}{x+2}-\frac {12}{x+2}=6-12\frac 1{x+2}\]

Obliczenia te pokazują, że wykres danej funkcji uzyskuje się poprzez skalowanie wykresu funkcji \(y=\frac{1}{x}\) w pionie o współczynnik 12, odwrócenie go względem osi poziomej i przesunięcie o 6 jednostek w górę i 2 jednostki w lewo.

Ten sam wynik można uzyskać, wykonując dzielenie wielomianowe licznika przez mianownik.

Rozwiązanie. Z uwagi przed ćwiczeniem 3 wiemy, że ogólna postać funkcji troficznej jest następująca: \[ y=\frac{Sx}{x+b}, \]

gdzie \(S\) jest wartością nasycenia drapieżnika, więc podstawiamy \(S=6\):

\[ y=\frac{6x}{x+b}. \]

Wartość parametru \(b\) możemy od razu określić na podstawie wyniku ćwiczenia 3, ale możemy ją również szybko obliczyć na podstawie drugiego warunku podanego w treści zadania. Wiemy, że

\[ 3=\frac{6\cdot 210}{210+b} \]

i stąd otrzymujemy \(b=210\). Ostateczna postać funkcji jest więc następująca:

\[ y=\frac{6x}{x+210}. \]

Bibliografia

Literatura

• Wikipedia, https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations 3 marca 2024 r.
• R Mařík, Dynamické modely populací (w języku czeskim), https://robert-marik.github.io/dmp/uvod.html, 3 marca 2024 r.
• D. Ludwig, D.D. Jones, C.S. Holling: Qualitative analysis of insect outbreak systems: the spruce budworm and forest, Journal of Animal Ecology 47(1): 315–332, luty 1978 r.

Źródła zdjęć

• https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations#/media/File:Lotka_Volterra_dynamics.svg
• https://www.npr.org/sections/thetwo-way/2016/08/11/489695842/once-nearly-extinct-california-island-foxes-no-longer-endangered Kevork Djansezian/AP