Previous ES TOC View on GitHub PDF PDF reduced EN CS ES PL SK Next ES

Funciones tróficas en modelos depredador-presa

Keywords: función, función fraccionaria racional, asíntota
20 min., 1/3

Los modelos matemáticos desempeñan un papel fundamental en el estudio de la naturaleza. Estos modelos permiten predecir desarrollos futuros, pero también cumplen otras funciones más importantes.

El uso de modelos ecológicos se denomina a veces métodos físicos en ecología, ya que el ecosistema se estudia desde la perspectiva del desarrollo poblacional y se emplean métodos matemáticos derivados originalmente de la resolución de problemas físicos. Los resultados de los modelos contienen, por ejemplo, la siguiente información.

  • Predicción La capacidad de trabajar con modelos matemáticos de ecosistemas nos permite predecir desarrollos futuros. Estos pueden ser desarrollos en un entorno inmutable o en un entorno en el que algunos parámetros cambian. El conocimiento del modelo nos permite evaluar el impacto de este cambio en el ecosistema.
  • Comprensión de los Principios Los modelos matemáticos permiten a los ecólogos y científicos estudiar las interacciones entre los diferentes componentes de los ecosistemas y comprender la dinámica de estos sistemas. Ayudan a identificar los factores que influyen en la estructura y el funcionamiento de estos ecosistemas.
  • Optimización de la toma de decisiones El modelado matemático de ecosistemas puede utilizarse para optimizar la toma de decisiones en áreas como la conservación de la biodiversidad o la gestión forestal y pesquera. Ayuda a identificar las mejores estrategias para alcanzar los objetivos establecidos.

Una de las relaciones fundamentales en los ecosistemas es la relación entre depredador y presa. Esta relación puede ser la única interacción en un ecosistema o complementarse con otras interacciones. La importancia de modelar la coexistencia depredador-presa se ilustrará con los siguientes modelos de importancia histórica.

Modelo Lotka-Volterra

En 1926, el matemático italiano Vito Voterra publicó uno de los primeros modelos depredador-presa. La motivación para construir este modelo fue el aumento del porcentaje de peces depredadores en las capturas durante las restricciones pesqueras de la Primera Guerra Mundial. Volterra fue informado por su yerno el biólogo marino Umberto D’Ancona, quien no pudo explicar el fenómeno Incluso esperaba lo contrario: un aumento en el porcentaje de especies de peces más pequeñas que sirven de alimento a los depredadores cuando se restringía la pesca. El modelo de Volterra explica este comportamiento como consecuencia de la simple idea de la interacción entre peces depredadores y presas.

El modelo contiene dos ecuaciones. La primera, que describe la población de presas, asume que esta crece de forma natural, pero los depredadores ralentizan su crecimiento. Un mayor número de depredadores provoca una mayor ralentización del crecimiento de las presas. Un exceso de depredadores puede incluso provocar la disminución del tamaño de la población de presas y su extinción. La ecuación dedicada a la población de depredadores asume que, sin presas, la población de depredadores se extinguiría. Sin embargo, cuantas más presas tengan disponibles los depredadores, mayor será la probabilidad de que esta extinción se traduzca en un aumento de la población de depredadores.

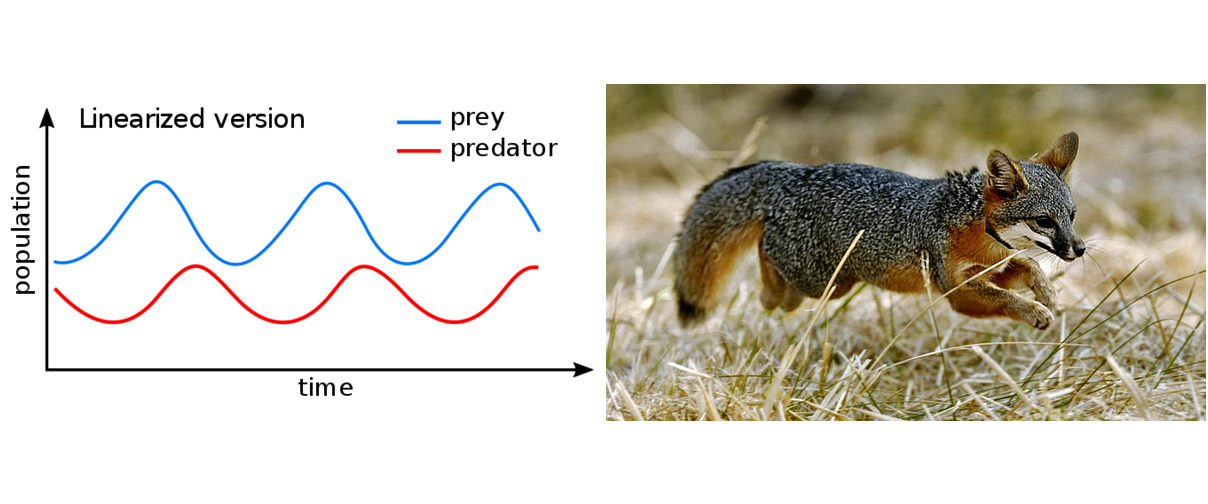
En el sistema descrito anteriormente, los ciclos surgen de forma natural. La abundancia de presas permite el crecimiento de la población de depredadores. Una alta cantidad de depredadores afecta negativamente a la población de presas, hasta el punto de que esta comienza a extinguirse. Esta mortandad resulta en falta de alimento para los depredadores, quienes también comienzan a extinguirse. Con el tiempo, la población de depredadores se reduce tanto que la presa apenas percibe su presencia. Por lo tanto, su población puede volver a crecer y multiplicarse hasta alcanzar su estado original. Sin embargo, esto permite que la población de depredadores crezca de nuevo, y el ciclo se completa. Los cambios periódicos en el tamaño de ambas poblaciones son claramente evidentes en los registros de compra de pieles de liebre americana y lince en la zona de la Bahía de Hudson.

El modelo de Volterra explicó no solo el origen de los ciclos, sino también que, al restringir la caza, el equilibrio en torno al cual oscilan las poblaciones de depredadores y presas se desplaza a favor del depredador y no de la presa. Este fenómeno, observado por D’Ancona, se denomina “efecto Volterra”.

El mismo modelo que Volterra fue propuesto en 1910 por el matemático estadounidense Alfred J. Lotka, razón por la cual el modelo ahora se llama modelo Lotka-Volterra.

Figura 1. A la izquierda, una progresión típica del tamaño de las poblaciones de depredadores y presas. Un pico de presas es seguido por un pico de depredadores y luego un declive en ambas poblaciones. A la derecha, un zorro isleño, que pasó de ser el principal depredador de su isla a ser una presa al borde de la extinción

Modelo de envoltura de abeto

Fluctuaciones periódicas similares a las del modelo Lotka-Volterra se observan n los bosques canadienses. En este caso, tras aproximadamente 30 a 40 años se produjo una sobrepoblación masiva de la mariposa cogollera (Choristoneura fumiferana). La población de esta mariposa es relativamente pequeña, pero en algunos años se multiplica por mil y sus orugas pueden matar hasta el 80 % de los árboles de un bosque, prácticamente destruyéndolo. Uno de los últimos casos masivos ocurrió en Quebec en 2006. Para 2019, se habían visto afectadas aproximadamente 9,6 millones de hectáreas de bosque 1, una superficie mayor que la de Hungría.

En 1978, los científicos D. Ludwig, D. D. Jones y C. S. Holling propusieron un modelo que no solo podía modelar el desarrollo de la población de polillas, sino que también ayudaba a explicar las razones por las que se produce la superpoblación descrita. La razón era la depredación. En este caso, era el consumo de orugas de polilla por las aves. Las aves sirvieron en la naturaleza como un factor que limitaba el número de orugas, pero solo hasta cierto límite. Cuando el bosque creció lo suficiente, también proporcionó suficiente alimento para la población de orugas. La población de orugas creció entonces hasta tal punto que las aves alcanzaron su punto de saturación en el consumo de alimentos y no pudieron reducir aún más la población de orugas. Esto hizo que el papel de las aves como depredadores fuera menos significativo y la población de orugas pudiera multiplicarse muy rápidamente y luego devastar el bosque.

En este caso, la depredación es importante para limitar la población de orugas. Dado que las aves, como depredadoras, tienen un ciclo reproductivo mucho más lento que la oruga, su población puede considerarse constante. Gracias a la saturación, las aves pueden limitar la tasa de crecimiento de la oruga solo hasta cierto punto. Sin embargo, esta limitación ya no es suficiente más allá de cierto tamaño de la población de orugas, que comienza a multiplicarse sin control.

Modelo del zorro isleño

El zorro isleño (Urocyon littoralis) es una especie animal única, endémica de las islas que rodean California. Tiene el tamaño de un gato y, debido a la ausencia de enemigos naturales, es confiado. Como especie es sensible y vulnerable debido a su baja variabilidad genética y baja resistencia a enfermedades introducidas desde el continente. Es uno de los cánidos más pequeños. Sin embargo, a diferencia de otros, puede trepar a los árboles.

Debido a las actividades humanas, la población de zorros isleños se vio seriamente afectada a principios del milenio. En la isla de San Miguel, la población disminuyó de 450 adultos en 1994 a 15 en 1999 2. Una situación similar se observó en las islas circundantes, cada una habitada por una subespecie distinta de zorro isleño. La causa de la muerte fue una serie de acontecimientos: la producción del insecticida DDT en la década de 1940 provocó la extinción del águila calva (Haliaeetus leucocephalus) y fue reemplazada por el águila real (Aquila chrysaetos). El depredador que se alimentaba de peces fue reemplazado en la isla por un depredador que prefiere los mamíferos. Esto fue fatal para el zorro isleño. Los zorros, anteriormente grandes depredadores, se convirtieron repentinamente en presas y, a principios del milenio, se encontraron al borde de la extinción. Y a diferencia del modelo de Lotka-Volterra, no era posible esperar que los zorros volvieran a sus niveles originales debido a las oscilaciones, porque las águilas también tenían alimento alternativo en forma de jabalíes y zorrillos.

Afortunadamente, gracias a inmensos esfuerzos, se logró salvar la especie de zorros isleños. Primero, se identificaron correctamente las causas de su declive. Después, bastó con repoblar la población de zorros y asegurar condiciones estables. Esto incluyó el exterminio de jabalíes, la reubicación de águilas reales, el regreso de las águilas calvas, la cría artificial de zorros, su retorno a la naturaleza y su vacunación contra las enfermedades introducidas. Todo esto se logró en un tiempo récord, en tan solo una década. Fue uno de los programas de rescate de mamíferos más exitosos.

Funciones tróficas

Un componente importante de los modelos depredador-presa, en cualquiera de los casos anteriores, es la “función trófica”. Esta función modela la acción de un solo depredador sobre una población de presas. Indica la tasa a la que un solo depredador ralentiza el crecimiento de las presas. Si \(x\) es el tamaño de la población de presas e \(y\) es la velocidad a la que un solo depredador ralentiza el crecimiento de las presas (es decir, la cantidad de presas capturadas por el depredador por unidad de tiempo), podemos escribir esta función matemáticamente en la forma \[ y=f(x). \] Intentaremos encontrar los supuestos naturales que debe satisfacer la función trófica. Luego, intentaremos encontrar una forma analítica adecuada para ella.

Tarea 1. Las suposiciones sobre el efecto de un depredador sobre su presa se reflejan en las características que debe tener una función trófica.

  1. Un depredador en un entorno con escasez de alimento también tiene pocas presas. Un mayor número de presas implica un acceso más fácil a ellas y, por lo tanto, una mayor captura.
  2. Sin alimento, un depredador no capturará nada. Si la cantidad de presas es cero, la cantidad de presas que un depredador captura por unidad de tiempo también es cero.
  3. Los depredadores consumen alimento solo hasta su saturación. Si hay abundancia de alimento, los depredadores no capturarán más alimento por unidad de tiempo de lo que corresponde a su saturación.

Expresa estas propiedades usando los términos que usamos para describir las propiedades de las funciones. ¿A qué propiedades de las funciones corresponde cada uno de los siguientes puntos?

Solución.

  1. La función \(y=f(x)\) es creciente.

  2. La función \(y=f(x)\) pasa por el origen, es decir se cumple \(f(0)=0\).

  3. La función \(y=f(x)\) está acotada verticalmente. Dado que la función es creciente y acotada verticalmente, su gráfica tiene una asíntota horizontal en el infinito.

Función trófica de Holling de tipo II

La función trófica indica la cantidad de presas que un depredador mata por unidad de tiempo para un tamaño de población dado. Por lo tanto, debe definirse en un conjunto de números no negativos, y los valores funcionales serán no negativos (esto también se deduce de los puntos 1 y 2 del problema anterior). En la sección anterior, se demostró que la función trófica debe pasar por el origen y crecer hasta una asíntota horizontal (crecimiento y acotación desde arriba). Estas propiedades no se cumplirán si buscamos una función trófica entre funciones lineales. Probemos, pues, con la función no lineal más simple: la proporcionalidad indirecta.

Figura 2. A la izquierda, dos funciones tróficas típicas, llamadas funciones de tipo Holling. La función de tipo II crece cada vez más lentamente. La función de tipo III crece lentamente al principio, se acelera y luego se ralentiza. A la derecha, la función de tipo II como parte de un gráfico de proporcionalidad inversa transformado. (Imagen propia)

Tarea 2. Comienza con la gráfica de la función \(y=\frac 1x\). En esta función, realiza transformaciones que modifiquen la gráfica como se describe a continuación.

  1. Reescala la gráfica \(k\) veces en dirección vertical. Esto no cambiará la monotonía ni la posición de la asíntota horizontal, pero sí la tasa de crecimiento.
  2. Invierte la gráfica sobre el eje horizontal y desplázala \(S\) hacia arriba. Esto garantizará que, para \(x\) positivo, la función sea creciente y crezca hasta la asíntota \(S\).
  3. Después de las transformaciones anteriores, la gráfica tiene una asíntota vertical en cero y una intersección con el eje horizontal a la derecha del origen. Desplaza la gráfica hacia la izquierda para que la asíntota vertical esté a la izquierda del eje vertical y la intersección con el eje \(x\) se mueva al origen.

Solución. La función cuyo gráfico se crea al reescalar \(y=\frac{1}{x}\) verticalmente \(k\) veces es \[y=\frac{k}{x}.\] La inversión se logra multiplicando la función por el factor \(-1\) y el desplazamiento se logra sumando el valor \(S\). Con estas modificaciones, obtenemos la función \[ y=S-\frac{k}{x}. \] El desplazamiento a la izquierda de \(b\) se logra sustituyendo \(x+b\) por la expresión \(x\). Esto nos da la función \[y=S-\frac {k}{x+b}.\] Tras convertirla a un denominador común la función tiene la forma \[ y=\frac{Sx+Sb}{x+b}-\frac{k}{x+b}=\frac{Sx + (Sb-k)}{x+b}. \] Para \(f(0)=0,\) se debe cumplir la condición \[ Sb-k=0. \] Esta condición muestra que las tres constantes no son independientes, sino que existe una relación entre ellas.

Nota. En el problema anterior, derivamos la forma analítica de una de las funciones tróficas básicas. Se trata de una función creciente que inicialmente crece hacia una asíntota horizontal y cuya tasa de crecimiento disminuye gradualmente. Esta función se denomina función de Holling de tipo II Se suele escribir en la forma \[f(x)=\frac {Sx}{x+b},\tag{1}\] donde \(S\) es el nivel de saturación y \(b\) es una constante, cuyo significado se explicará en la siguiente tarea.

Tarea 3. Demuestre que para un tamaño de población igual a \(b\) el valor de la función trófica (1) es igual a la mitad del valor de saturación.

Solución. Por sustitución directa en (1) obtenemos \[ f(b)=\frac{Sb}{b+b}=\frac {Sb}{2b}=\frac S2. \] Esto demuestra la afirmación.

El siguiente problema muestra el proceso opuesto, donde a partir de la función trófica en la forma (1) derivamos una forma que muestra las transformaciones sucesivas de la función \(y=\frac 1x\).

Tarea 4. Modifica la fórmula de la función \[y=\frac {6x}{x+2}\] a su forma básica, es decir, de modo que podamos leer las transformaciones sucesivas de la función \(y=\frac 1x\) en la gráfica de la función dada.

Solución. Resolvemos el problema modificando ingeniosamente la fracción. En el numerador, creamos un múltiplo del denominador, dividimos la fracción entre dos y reducimos:

\[\frac {6x}{x+2} = \frac {6(x+2)-12}{x+2}=\frac {6(x+2)}{x+2}-\frac {12}{x+2}=6-12\frac 1{x+2}\]

Este cálculo muestra que la gráfica de la función dada se obtiene extendiendo la gráfica de la función verticalmente doce veces, girándola alrededor del eje horizontal y desplazándola seis unidades hacia arriba y dos unidades hacia la izquierda.

Podríamos obtener el mismo resultado dividiendo el denominador por el numerador.

Tarea 5. Construye una función trófica si sabes que la tasa de consumo de alimentos en la saturación del depredador es \(6\), y que el consumo ocurre a la mitad de la tasa para una población de presas de tamaño \(210\).

Solución. Gracias a la nota anterior al tercer problema sobre la forma general de la función trófica, sabemos que la prescripción será de la forma \[ y=\frac{Sx}{x+b}, \] donde \(S\) es el valor de saturación del depredador, es decir, \[ y=\frac{6x}{x+b}\,. \] Podemos decir inmediatamente el valor del parámetro \(b\) gracias al Problema 3, pero también podemos calcularlo rápidamente a partir de la segunda condición de la asignación, ya que sabemos que \[ 3=\frac{6\cdot 210}{210+b} \] y de aquí se sigue \(b=210\). Por lo tanto, la prescripción de la función resultante es \[ y=\frac{6x}{x+210}. \]

Bibliografía y referencias

Bibliografía

Fuentes de las imágenes

  1. Ver fuente https://www.nrcan.gc.ca.↩︎

  2. Ver fuente https://www.iucnredlist.org/species/22781/13985603.↩︎