Ciśnienie krwi

45 min., 2/3

Funkcje trygonometryczne i zjawiska okresowe

Podstawowe funkcje trygonometryczne sinus i cosinus są często wykorzystywane do modelowania fal świetlnych, dźwiękowych i elektromagnetycznych. Są one również wykorzystywane do aproksymacji ¹ innych zjawisk okresowych, takich jak pływy lub ciśnienie krwi.

Zrozumienie tych funkcji (i ich poszczególnych składników) pozwala nam skutecznie przewidywać i analizować zjawiska okresowe oraz ich właściwości. Możemy na przykład obliczyć wysokość fal oceanicznych lub czas przypływu. W poniższym tekście skupimy się na funkcjach przybliżających ciśnienie krwi.

Podstawowe informacje o ciśnieniu krwi

Serce działa jak pompa, która pompuje natlenioną krew przez naczynia krwionośne w całym organizmie, dostarczając mu niezbędny tlen i składniki odżywcze. Ciśnienie krwi to ciśnienie, jakie krew wywiera na ścianki naczyń krwionośnych, przez które przepływa. Ciśnienie to różni się w różnych częściach układu krążenia. Zazwyczaj, gdy mówimy o ciśnieniu krwi, mamy na myśli ciśnienie tętnicze — ciśnienie w dużych tętnicach. Zbyt wysokie ciśnienie krwi obciąża tętnice (i serce), co może prowadzić do zawału serca lub udaru mózgu.

Wysokie ciśnienie krwi, znane również jako nadciśnienie, jest czymś, czego zazwyczaj nie czujemy ani nie zauważamy. Często nie daje wyraźnych objawów ani sygnałów ostrzegawczych. Jedynym sposobem, aby poznać swoje ciśnienie krwi, jest jego pomiar. Pierwsze urządzenia pomiarowe określały ciśnienie krwi na podstawie wysokości słupa rtęci, dlatego wartości nadal podaje się w milimetrach słupa rtęci. Ciśnienie krwi zapisuje się jako stosunek dwóch liczb. Na przykład, jeśli odczyt wynosi 120/80 mm Hg, ciśnienie krwi wynosi 120 na 80.

Wyższa liczba oznacza ciśnienie skurczowe. Jest to maksymalne ciśnienie osiągane, gdy serce kurczy się i pompuje krew do układu krążenia. Niższa liczba to ciśnienie rozkurczowe, czyli minimalne ciśnienie osiągane, gdy mięsień sercowy rozluźnia się między uderzeniami.

Poniższa tabela ciśnienia krwi przedstawia zakresy wysokiego, niskiego i zdrowego ciśnienia krwi.

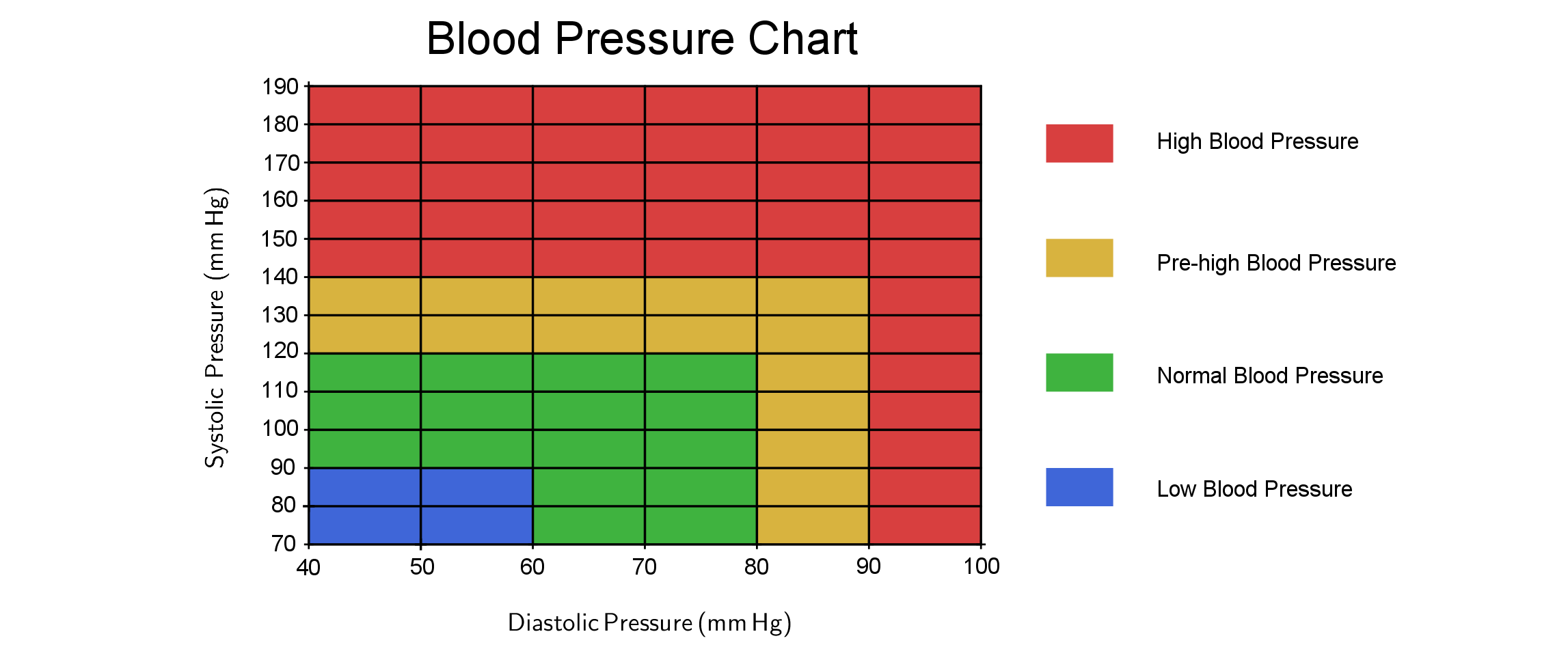
Przybliżenie funkcji ciśnienia krwi

Podczas skurczów serca ciśnienie krwi wzrasta i opada w powtarzającym się cyklu. Czas trwania jednego uderzenia serca odpowiada okresowi funkcji reprezentującej ciśnienie krwi. Każdy okres funkcji ciśnienia krwi odpowiada jednemu uderzeniu serca (informuje nas, ile czasu zajmuje pełny cykl uderzeń serca). Ponadto wiemy, że lokalne maksimum funkcji reprezentuje wartość ciśnienia skurczowego, natomiast lokalne minimum odpowiada ciśnieniu rozkurczowemu. Funkcję ciśnienia krwi możemy przybliżyć za pomocą funkcji sinusoidalnej lub cosinusoidalnej. Przypomnijmy, że ogólna postać funkcji sinusoidalnej to

\[ f\left(x\right) = a\cdot\sin\left(bx + c\right) +d, \]

gdzie \(a\) reprezentuje amplitudę, która określa, jak daleko fala sinusoidalna przesuwa się powyżej lub poniżej swojej średniej pozycji. Wartość \(b\) wpływa na okres funkcji (okres jest określony przez \(\frac{2\pi}{|b|}\).). Współczynnik \(c\) określa przesunięcie w kierunku osi \(x\), a \(d\) przesunięcie w kierunku osi \(y\).

Rozwiązanie. Okres \(p_1\) funkcji \(P_1\) można obliczyć jako

\[p_1=\frac{2\pi}{\frac{7\pi}{3}}=\frac{6}{7}\,\text{seconds}.\]

Ponieważ czas trwania jednego uderzenia serca wynosi \(\frac{6}{7}\) sekundy, częstość akcji serca \(f_1\) wynosi

\[ f_1=\frac{60}{\frac{6}{7}}=70\,\text{uderzeń na minutę}. \]

Podobnie dla funkcji \(P_2\) okres wynosi

\[ p_2=\frac{2\pi}{2\pi}=1\,\text{second}. \]

Tętno wynosi zatem \(f_2=60\) uderzeń na minutę.

Rozwiązanie.
Aby wykreślić wykres funkcji, oś \(x\) reprezentuje czas \(t\) w sekundach. Oś \(y\) reprezentuje ciśnienie krwi \(P\) w milimetrach słupa rtęci. Jednostki na osiach powinny być tak dobrane, aby wykres był przejrzysty i łatwy do interpretacji. Na przykład dobrym wyborem jest, aby jedna jednostka na osi \(x\) odpowiadała stu jednostkom na osi \(y\). Na wykresie pokazanym w przykładzie stosunek jednostek na osiach wynosi \(1:125\). Funkcja

\[ P_1=25\cdot\sin\left(\frac{7\pi}{3}t\right)+105 \]

oscyluje wokół wartości 105, a jej amplituda wynosi 25. Zatem lokalne wartości maksymalne funkcji (ciśnienie skurczowe) wynoszą: 105+25=130, a lokalne wartości minimalne (ciśnienie rozkurczowe) wynoszą: 105-25=80.

Funkcja

\[ P_2=30\cdot\cos\left(2\pi t\right)+125 \]

oscyluje wokół wartości 125, z amplitudą 30. Jego lokalne wartości maksymalne wynoszą: 125+30=155 (ciśnienie skurczowe), a lokalne wartości minimalne wynoszą: 125-30=95 (ciśnienie rozkurczowe).

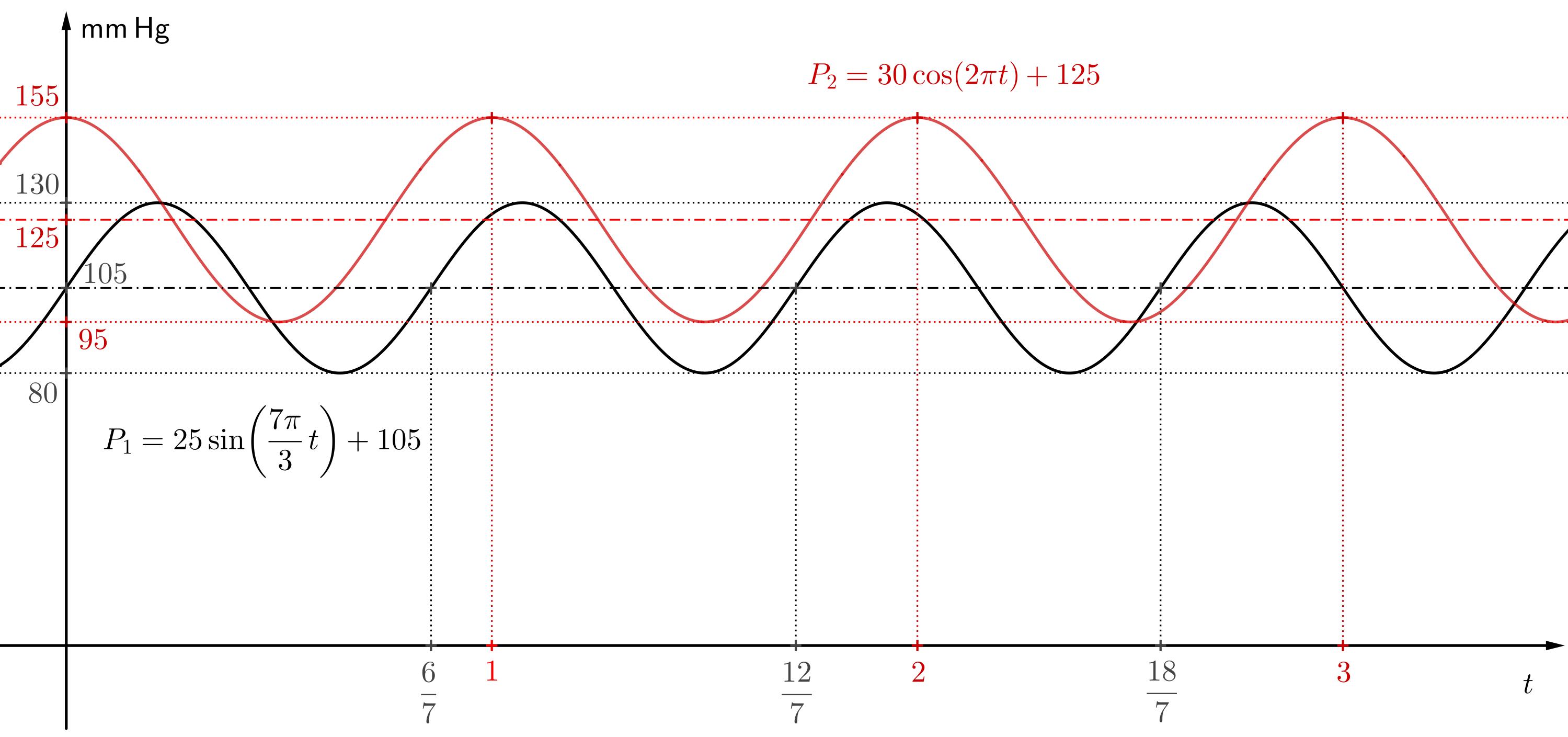
Funkcja \(P_1\) odpowiada ciśnieniu krwi wynoszącemu około \(130\) na \(80\). Zgodnie z tabelą zamieszczoną we wstępie odpowiada to wartościom granicznym między ciśnieniem normalnym a wysokim (w niektórych krajach jest to ciśnienie normalne, w innych już dolna granica wysokiego ciśnienia). Funkcja \(P_2\) odpowiada ciśnieniu \(155\) na \(95\), co wyraźnie mieści się w zakresie wysokiego ciśnienia krwi.

Wizualizacja takich wykresów pomaga nam zrozumieć zmiany ciśnienia krwi i inne zjawiska cykliczne, co jest niezbędne zarówno w matematyce, jak i w praktycznych zastosowaniach.

Wysokie ciśnienie krwi jest stanem niebezpiecznym i głównym czynnikiem ryzyka chorób serca i udaru mózgu. Zdrowy tryb życia — na przykład spożywanie dużej ilości owoców i warzyw, ograniczenie spożycia sodu i aktywność fizyczna — może pomóc w zapobieganiu wysokiemu ciśnieniu krwi. Wysoka wartość pojedynczego pomiaru niekoniecznie oznacza, że masz wysokie ciśnienie krwi, ponieważ na ciśnienie krwi może wpływać wiele czynników w ciągu dnia, takich jak temperatura, pora ostatniego posiłku lub stres. Wykreślając funkcje \(P_1\) i \(P_2\), od razu widzimy różnice między nimi. Czasami jednak dwie funkcje, które na pierwszy rzut oka wydają się różne, mogą w rzeczywistości tworzyć ten sam wykres. Czy potrafisz od razu stwierdzić, że poniższe dwie funkcje mają identyczne wykresy?

\[ y=\sin\frac{3x}{5},\qquad y=\cos\left(\frac{3x}{5}-\frac{\pi}{2}\right) \]

Te dwie funkcje mają ten sam wykres, a okres obu funkcji wynosi

\[ \frac{2\pi}{\frac{3}{5}}=\frac{10\pi}{3}. \]

Ale uwaga: wykres funkcji \(y=\cos\left(\frac{3x}{5}-\frac{\pi}{2}\right)\) nie jest przesunięty o \(\frac{\pi}{2}\) w prawo w porównaniu z wykresem funkcji \(y=\cos\frac{3x}{5}\), mimo że z wyrażenia mogłoby się tak wydawać. Zamiast tego jest on przesunięty o jedną czwartą okresu funkcji. Możemy to zobaczyć, jeśli przepisujemy wzór:

\[ y=\cos\left(\frac{3x}{5}-\frac{\pi}{2}\right)=\cos\left(\frac{3}{5}\left(x-\frac{5\pi}{6}\right)\right) \]

Aby porównać takie funkcje, często przydatne jest przekształcenie jednej funkcji do postaci drugiej. Właśnie tym zajmiemy się w następnym ćwiczeniu.

Rozwiązanie. Dla funkcji podstawowych \(\sin x\) i \(\cos x\) mamy tożsamość:

\[ \sin x=\cos\left(x-\frac{\pi}{2}\right), \]

gdzie \(\frac{\pi}{2}\) stanowi jedną czwartą okresu. Okres funkcji \(P_1\) wynosi \(p_1=\frac{6}{7}\), a jedna czwarta tego okresu wynosi

\[ \frac{p_1}{4}=\frac{6}{28}=\frac{3}{14}. \]

Korzystając z tego, możemy zapisać:

\[ \sin\left(\frac{7\pi}{3}t\right)=\cos\left(\frac{7\pi}{3}\left(t-\frac{3}{14}\right)\right) \]

a funkcja \(P_1\) może być wyrażona jako:

\[ P_1=25\cdot\cos\left(\frac{7\pi}{3}t-\frac{1}{2}\pi\right)+105. \]

W poprzednim ćwiczeniu mogliśmy również pójść w drugą stronę i wyrazić funkcję \(P_2\) za pomocą funkcji sinusoidalnej zamiast cosinusoidalnej.

Rozwiązanie. Aby przybliżyć funkcję ciśnienia krwi, użyjemy funkcji sinusoidalnej (rozwiązanie z wykorzystaniem funkcji cosinusowej byłoby podobne).

Amplituda funkcji wynosi \(\frac{110-70}{2}=20\), a funkcja oscyluje wokół wartości środkowej \(\frac{110+70}{2}=90\).

Okres funkcji wynosi

\[ p=\frac{60}{50}=\frac{6}{5}, \]

co oznacza, że jedno uderzenie serca trwa 1,2 sekundy. Wykorzystując wzór na okres p:

\[ p=\frac{2\pi}{b} = 1{.}2 \]

znajdujemy: \(b= \frac{5}{3}\pi\).

Wartość \(c\) można wybrać dowolnie, najprościej jest wybrać \(c = 0\). Podstawiając powyższe wartości do ogólnego wzoru funkcji, otrzymujemy

\[ P(t) = 20\cdot\sin\left(\frac{5\pi}{3}t\right)+90. \]

Ta funkcja w przybliżeniu modeluje ciśnienie krwi osoby o określonych wartościach jako funkcję czasu (w sekundach).

Technika osłuchiwania do pomiaru ciśnienia krwi

Na zakończenie pokrótce wyjaśnijmy, jak mierzy się ciśnienie krwi w rzeczywistości. Jedną z dokładnych metod jest tak zwana technika osłuchiwania. Metoda ta wykorzystuje ciśnieniomierz składający się z gumowego mankietu, nadmuchiwanego pęcherza, manometru (mechanicznego miernika ciśnienia) i stetoskopu.

Mankiet gumowy umieszcza się mniej więcej w połowie ramienia. Ciśnienie w mankiecie zwiększa się do wartości wyższej niż ciśnienie w tętnicy, co powoduje sztuczne zablokowanie przepływu krwi. Poprzez stopniowe i powolne zmniejszanie ciśnienia w mankiecie, w pewnym momencie przywracany jest przepływ krwi.

Początkowo wysokie ciśnienie w mankiecie powoduje deformację tętnicy, co sprawia, że początkowy przepływ krwi jest burzliwy. Ciśnienie, przy którym bicie serca staje się słyszalne przez stetoskop, odpowiada skurczowemu ciśnieniu krwi.

Dźwięki są słyszalne tak długo, jak długo ciśnienie w mankietce jest wystarczające, aby zdeformować tętnicę i tym samym utrzymać burzliwy przepływ. Gdy ciśnienie w mankietce spadnie tak nisko, że nie wystarcza już do deformacji tętnicy, pierwotny przepływ krwi zostaje przywrócony, a dźwięki zanikają. Ciśnienie, przy którym dźwięki są słyszalne po raz ostatni, odpowiada rozkurczowemu ciśnieniu krwi.

Udoskonalenie

Warto zauważyć, że bardziej realistyczne modele funkcji ciśnienia krwi są bardziej złożone. Wymagają one zastosowania sum funkcji trygonometrycznych o różnych okresach.

Poniższy rysunek przedstawia konkretny przykład takiej sumy i odpowiadający jej wykres. Rysunek pokazuje również, w jaki sposób mierzy się ciśnienie krwi. Szybkość opróżniania mankietu jest w przybliżeniu stała. Ciśnienie w mankiecie spada zatem w stałym tempie (w przybliżeniu) i jest przedstawione na rysunku jako linia prosta.

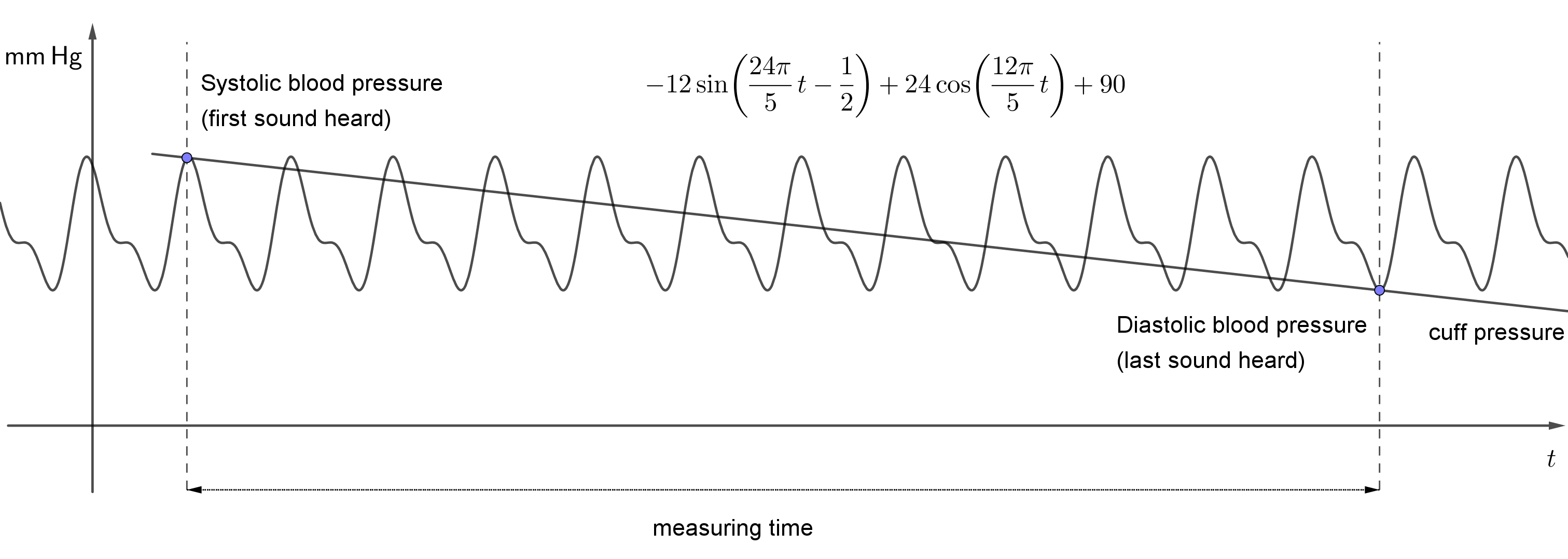
Udoskonalenie funkcji ciśnienia krwi przy użyciu sum sinusów i cosinusów jest związane z twierdzeniem Fouriera, które mówi, że każda funkcja okresowa ciągła może być wyrażona jako nieskończona suma funkcji sinusoidalnych i cosinusoidalnych — każda o określonej amplitudzie i okresie.

Wynik ten został odkryty w 1822 roku przez francuskiego matematyka Josepha Fouriera w ramach rozwiązania równania przewodzenia ciepła. Jest to kluczowa koncepcja w analizowaniu i rozumieniu wszelkiego rodzaju zjawisk okresowych. Twierdzenie Fouriera stanowi podstawę współczesnego przetwarzania sygnałów.

Literatura

• https://www.vaia.com/en-us/textbooks/math/calculus-an-applied-approach-8-edition/chapter-8/problem-72-health-the-function-p100-20-cos-5-pi-t-3-approxim/
• https://www.vaia.com/en-us/textbooks/math/precalculus-9-edition/chapter-4/problem-90-the-function-p100-20-cos-frac5-pi-t3-approximates/#short-answer
• https://www.bloodpressureuk.org/your-blood-pressure/understanding-your-blood-pressure/what-do-the-numbers-mean/