Vektory
 30 min.,
30 min.,  2/3
2/3 Vektory predstavujú dôležitý pojem nielen v matematike, ale aj vo fyzike či informatike. V matematike sa nimi zaoberá lineárna algebra.
Normálne možno vektor definovať ako prvok vektorového priestoru, čo je abstraktná algebraická štruktúra so zavedenými operáciami sčítania vektorov a násobenia vektora skalárom. Typickým príkladom takéhoto priestoru je množina všetkých usporiadaných \(n\)-tíc reálnych čísel, teda napríklad dvojíc alebo trojíc, s príslušnými operáciami.
Na strednej škole sa však vektor často predstavuje názorne ako množina všetkých orientovaných úsečiek s rovnakou veľkosťou (dĺžkou) a rovnakým smerom.
Vo fyzike majú vektory zásadný význam pri popise veľkosti a smeru rôznych veličín, napríklad rýchlosti, zrýchlenia, síl pôsobiacich na teleso alebo elektromagnetických polí.
V informatike sa pod pojmom vektor spravidla rozumie usporiadaný zoznam prvkov (nielen čísel), pričom tento dátový typ sa používa ako efektívny spôsob ukladania a spracovávania údajov, napríklad v aplikáciách strojového učenia.
Existuje však odvetvie informatiky, kde sa vektory uplatňujú v rovnakom význame, ako ho poznáme zo stredoškolskej matematiky alebo fyziky – je ním prostredie počítačových hier.
Schopnosť pracovať s vektormi patrí k najzákladnejším predpokladom programátora hier.
V závislosti od toho, či ide o 2D alebo 3D hru, majú vektory dve alebo tri súradnice. Uplatňujú sa pri reprezentácii geometrických vlastností objektov v hernom svete.
Zjednodušene sa preto obmedzíme na dvojrozmerný priestor, teda rovinu, a budeme pracovať v kartézskej súradnicovej sústave.
Poznámka: Takých základných stavebných kameňov je potrebných samozrejme oveľa viac. Okrem príslušného programovacieho nástroja je potrebné poznať aj matice transformácií, ako je posunutie, otočenie a podobne.
V nasledujúcich cvičeniach sa však sústredíme výhradne na operácie s vektormi.
Body a smerové vektory
V nasledujúcich príkladoch budeme rozlišovať zadanie bodov (v hranatých zátvorkách) a vektorov (v okrúhlych zátvorkách). Súčasne však budeme mať na pamäti, že bod \(A = [a_1;a_2]\) môžeme interpretovať aj ako koncový bod vektora \(\overrightarrow{a} = (a_1;a_2)\), ktorý má za počiatočný bod počiatok súradnicovej sústavy.
Bod je teda určený svojimi súradnicami, avšak na rozdiel od vektora ho neurčuje veľkosť (dĺžka) a smer. Bod \([0,0]\) alebo vektor \((0, 0)\) budeme chápať ako stred herného sveta.
Častým prípadom využitia vektorov je výpočet takého vektora, ktorý vyjadruje vzťah jedného objektu voči druhému. Uvažujme body \(A = [a_1;a_2]\) a \(B = [b_1;b_2]\). Vektor \(\overrightarrow{u}=\overrightarrow{AB}= (b_1-a_1; b_2-a_2)\) obvykle nazývame smerový vektor.
Ak budú body \(A\) a \(B\) v hre reprezentovať postavy, tak vektor \(\overrightarrow{AB}\) určuje smer a jeho veľkosť potom vzdialenosť, ktorú postava \(A\) musí prejsť, aby sa dostala k postave \(B\).
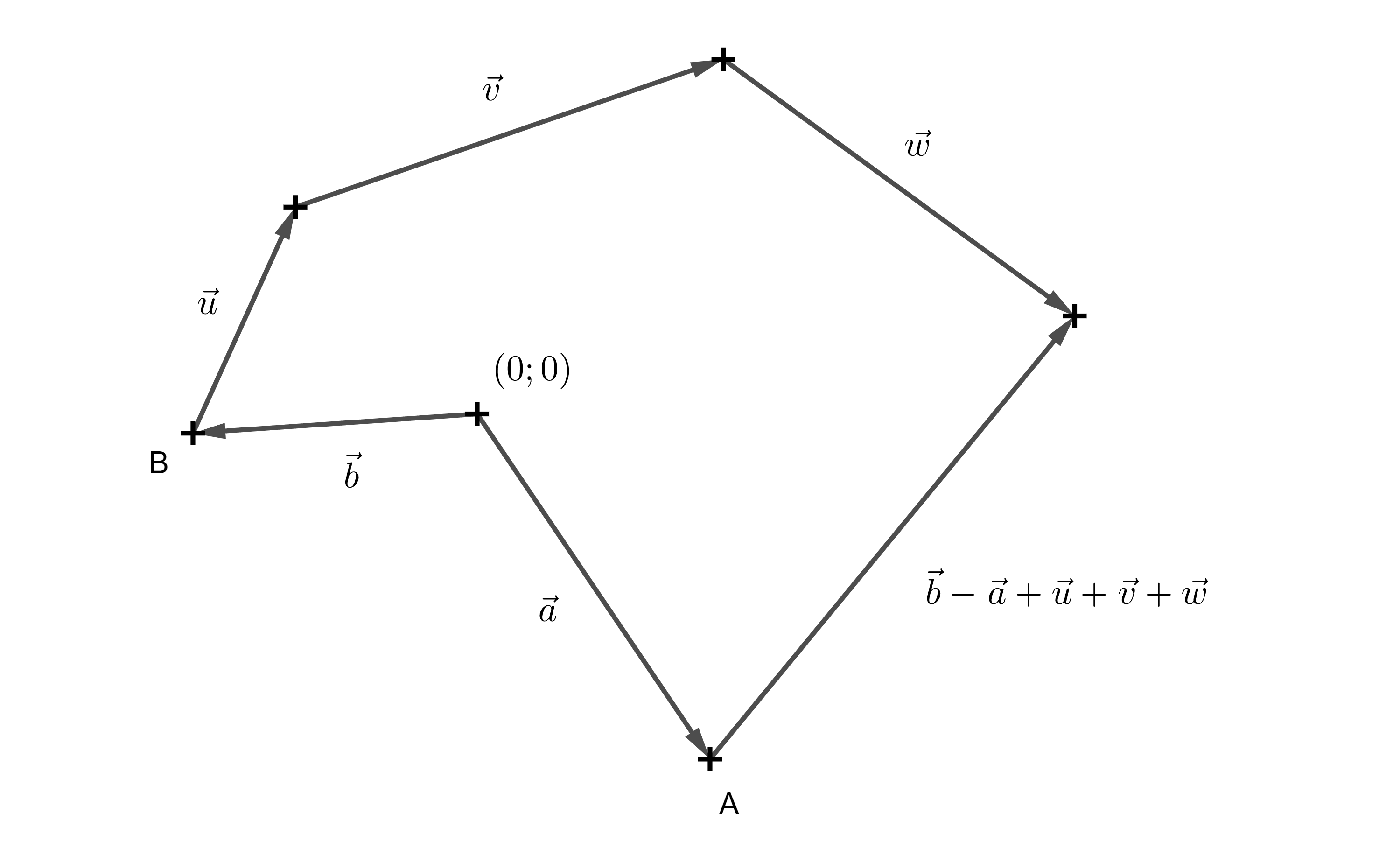
Úloha 1. V dvojrozmernej hre máme programátora, ktorý ovláda postavu \(A\) a hráča, ktorý ovláda postavu \(B\). Na začiatku sa obe postavy nachádzajú na rôznych miestach, pričom sú pre jednoduchosť reprezentované bodmi \(A\) a \(B\). Postava \(B\) sa následne pohybuje po dráhe určenou postupným posunutím v smeroch vektorov \(\overrightarrow{u}\), \(\overrightarrow{v}\) a \(\overrightarrow{w}\). Úlohou je vyjadriť vektor, ktorý musí programátor určiť na to, aby postava \(A\) mohla zasiahnuť postavu \(B\).
Riešenie. Je zrejmé, že postava \(B\) prešla celkovú trasu \(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}\). Postavy \(A\) a \(B\) sa však na začiatku nachádzali na rôznych miestach. Preto je potrebné určiť vektor s počiatočným bodom v bode \(A\) a koncovým bodom v bode \(B\), teda smerový vektor \(\overrightarrow{AB}\). Vieme, že bod \(A\) môžeme chápať ako koncový bod vektora \(\vec{a}\) a bod \(B\) ako koncový bod vektora \(\vec{b}\). Potom platí: \(\overrightarrow{AB} = \overrightarrow{b}-\overrightarrow{a}\) (Keďže bod a vektor majú rovnaké súradnice, často sa používa aj zápis \(\overrightarrow{AB} = B-A\)). Hľadaný vektor, ktorý určuje výstrel postavy \(A\) na postavu \(B\), je teda: \(\overrightarrow{b}-\overrightarrow{a}+\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}\).
Pri každej postave v hernom svete sa využíva aj vektor vo význame usporiadaného zoznamu položiek. Jednou z položiek môže byť napríklad meno postavy, jej úloha či poloha. Ďalšou vlastnosťou každej postavy v hernom svete je smer, ktorým je natočená. Na určenie tohto smeru sa používa takzvaný normalizovaný smerový vektor, teda smerový vektor s dĺžkou \(1\).
Normalizované smerové vektory sa zároveň využívajú na uchovávanie informácie o tom, akým smerom sa nachádzajú ostatné postavy alebo objekty. Poznámka: Dôvod, prečo sa v hernom svete používajú práve normalizované verzie smerových vektorov, si vysvetlíme neskôr.
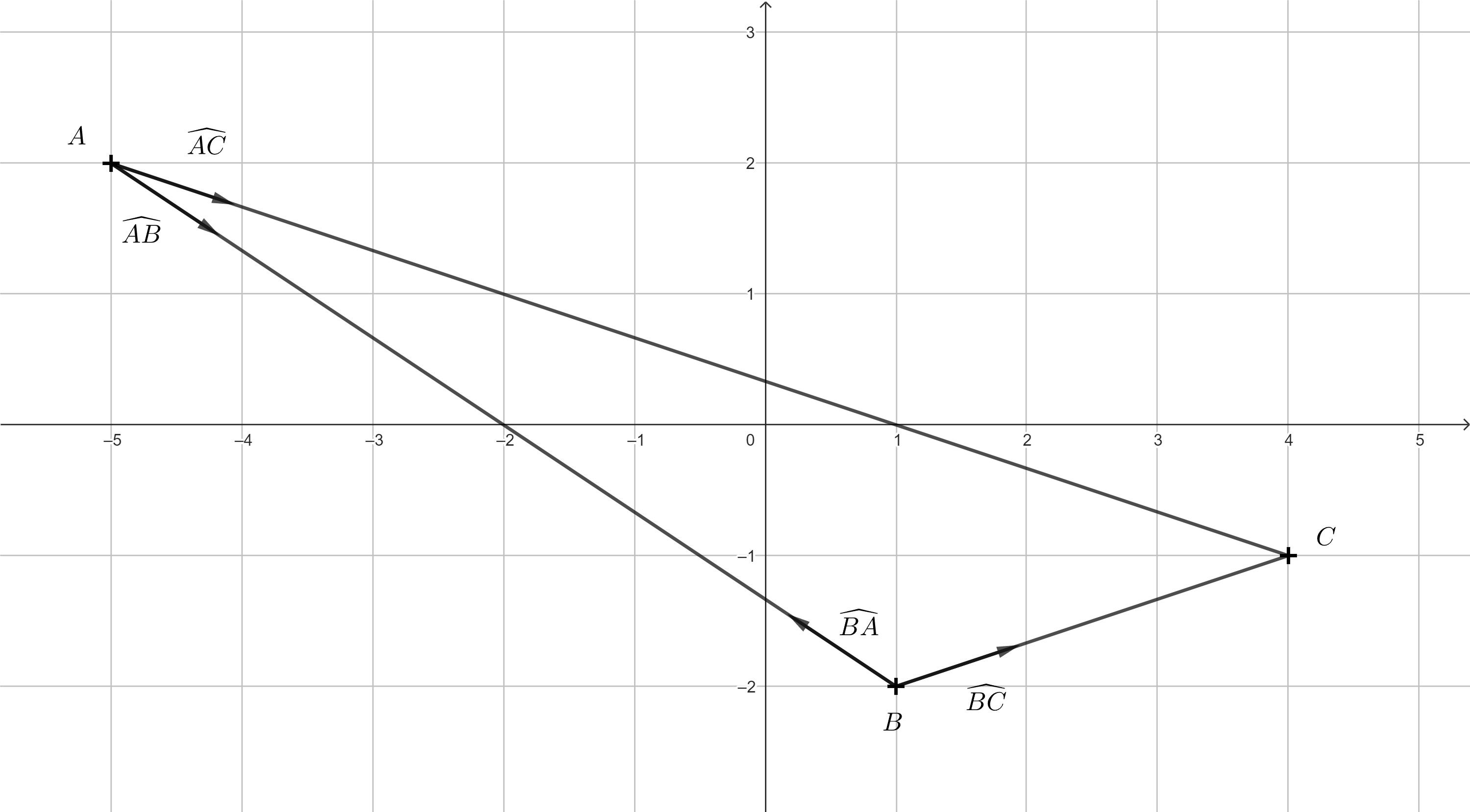
Úloha 2. Majme postavy \(A = [-5;2]\), \(B = [1;-2]\), \(C = [4;-1]\). Určite normalizované smerové vektory postáv \(A\) a \(B\) smerom k ostatným postavám. Nakreslite zodpovedajúci obrázok.
Riešenie. Pre smerový vektor \(\overrightarrow{AB}\) platí \(\overrightarrow{AB}= (1-(-5); -2-2) = (6;-4)\). Ak ho chceme normalizovať, stačí ho vydeliť jeho dĺžkou \(\left | \overrightarrow{AB} \right | = \sqrt{6^2+(-2)^2} = \sqrt{52}.\) Normalizovaný vektor k vektoru \(\overrightarrow{AB}\) označíme \(\widehat{AB}\) a platí
\[ \widehat{AB} = \frac{\overrightarrow{AB}}{\left | \overrightarrow{AB} \right | } = \frac{(6;-4)}{\sqrt{52}} = \left(\frac{3}{\sqrt{13}};-\frac{2}{\sqrt{13}}\right). \]
Podobne:
\[ \widehat{AC} = \frac{\overrightarrow{AC}}{\left | \overrightarrow{AC} \right | } = \frac{(9;-3)}{\sqrt{90}} = \left(\frac{3}{\sqrt{10}};-\frac{1}{\sqrt{10}}\right), \]
\[\widehat{BC} = \frac{\overrightarrow{BC}}{\left | \overrightarrow{BC} \right | } = \frac{(3;1)}{\sqrt{10}} = \left(\frac{3}{\sqrt{10}};\frac{1}{\sqrt{10}}\right),\]
\[\widehat{BA} = \frac{\overrightarrow{BA}}{\left | \overrightarrow{BA} \right | } = \frac{(-6;4)}{\sqrt{52}} = \left(-\frac{3}{\sqrt{13}};\frac{2}{\sqrt{13}}\right).\]
Vektor \(\widehat{BA}\) sme nemuseli počítať, keďže má rovnakú veľkosť ako \(\widehat{AB}\) ale opačný smer. Súradnice takýchto vektorov sa teda líšia iba znamienkom.
Úloha 3. Majme polohu postavy \(A = [a_1;a_2]\) a postavy \(B = [b_1;b_2]\) ktoré sa nachádzajú na rôznych miestach. Určte: a) normalizovaný smerový vektor \(\widehat{BA}\), b) kde sa bude postava \(A\) nachádzať potom, čo prejde tri jednotkové dĺžky smerom k postave \(A\)?
Riešenie. a) To, čo sme počítali v predchádzajúcom príklade s konkrétnymi súradnicami, teraz zapíšeme všeobecne. Teda \[\widehat{BA} = \frac{\overrightarrow{BA}}{\left| \overrightarrow{BA} \right| } = \frac{(a_1-b_1;a_2-b_2)}{\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}}.\]
- Z predchádzajúceho máme vypočítaný smerový vektor jednotkovej dĺžky. Teraz stačí vynásobiť ho tromi a pripočítať k polohe postavy \(B\). Dostaneme
\[B+3\cdot\widehat{BA} = [b_1;b_2] +3\frac{(a_1-b_1;a_2-b_2)}{\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}}.\]
Skalárny súčin a jeho použitie
Výsledkom skalárneho súčinu dvoch vektorov je skalár, teda reálne číslo. V programovaní hier má dôležité miesto skalárny súčin normalizovaných vektorov.
Úloha 4. Určte skalárne súčiny normalizovaných smerových vektorov z riešenia Úlohy 2.
Riešenie.
\[ \widehat{AB} \cdot \widehat{AC} = \left(\frac{3}{\sqrt{13}};-\frac{2}{\sqrt{13}}\right) \cdot \left(\frac{3}{\sqrt{10}};-\frac{1}{\sqrt{10}}\right) = \frac{9}{\sqrt{130}}+\frac{2}{\sqrt{130}} = \frac{11}{\sqrt{130}} \dot=0{,}96 \]
\[ \widehat{BA} \cdot \widehat{BC} = \left(-\frac{3}{\sqrt{13}};\frac{2}{\sqrt{13}}\right) \cdot \left(\frac{3}{\sqrt{10}};\frac{1}{\sqrt{10}}\right) = -\frac{9}{\sqrt{130}}+\frac{2}{\sqrt{130}} = -\frac{7}{\sqrt{130}} \dot= -0{,}054 \]
Skalárny súčin dvoch normalizovaných vektorov je veľmi užitočný, pretože určuje, do akej miery dva vektory smerujú rovnakým alebo podobným smerom! Hodnota skalárneho súčinu v tomto prípade môže nadobúdať hodnoty v intervale \(-1\) až \(1\), pričom \(1\) znamená, že oba vektory smerujú presne rovnakým smerom, a \(-1\), že smerujú opačným smerom a hodnota blízka \(0\) vyjadruje, že zvierajú uhol blízky pravému uhlu. Dôvodom tohto intervalu \(-1\) až \(1\) je, že ide o funkčné hodnoty funkcie kosínus. Pre skalárny súčin dvoch vektorov \(\vec{p}\), \(\vec{q}\), totiž platí vzťah
\[ \vec{p} \cdot \vec{q}=\left | \vec{p} \right |\left | \vec{q} \right |\cos\alpha, \]
kde \(\alpha\) je uhol, ktorý vektory \(\vec{p}\) a \(\vec{q}\) zvierajú.
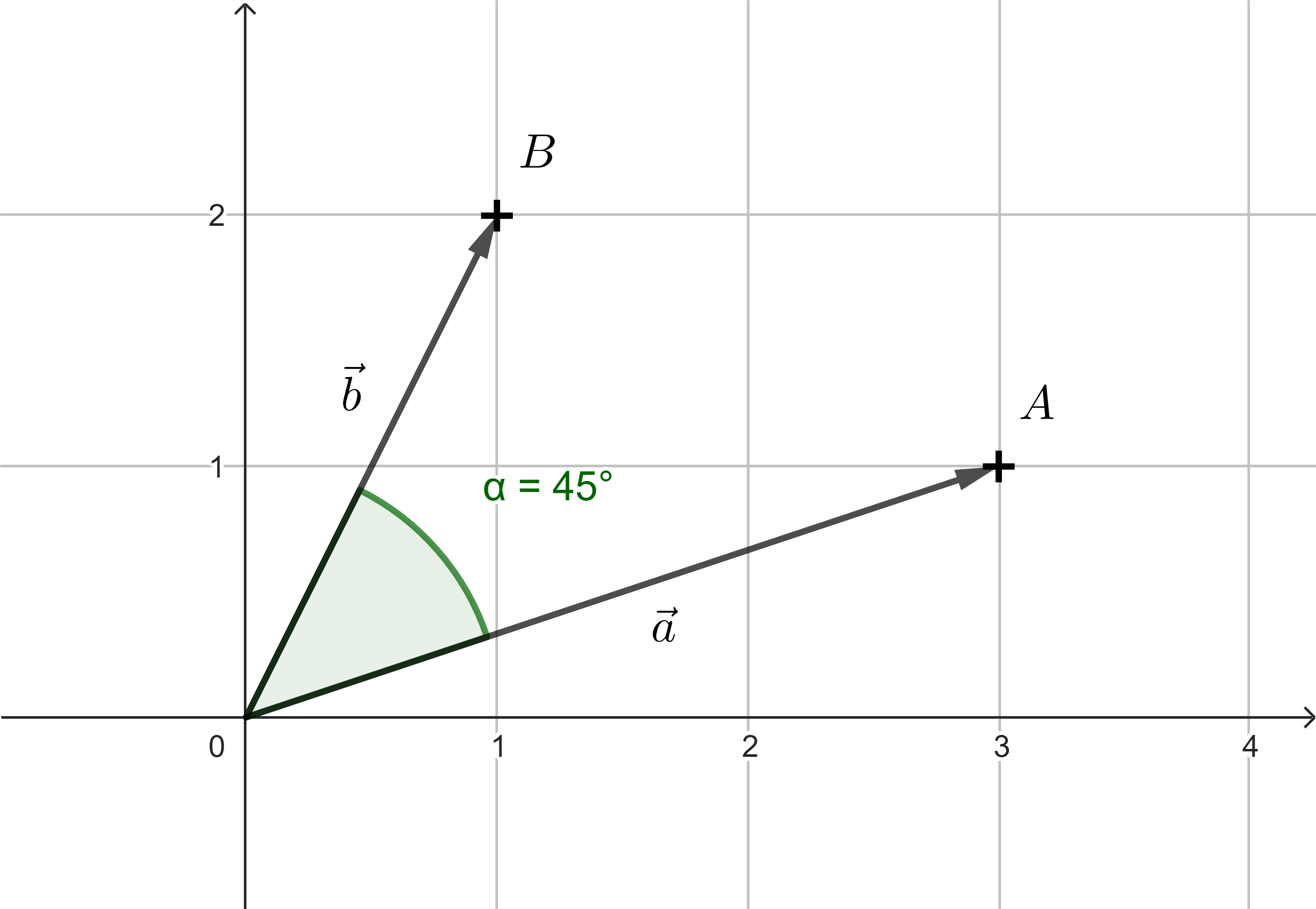
Úloha 5. Pozorovateľ v počiatku súradnicovej sústavy sa pozerá na objekt \(A=[3;1]\), Určte uhol \(\alpha\) o ktorý sa musí otočiť, aby smer jeho pohľadu mieril priamo na objekt \(B=[1;2]\).
Riešenie. Body \(A\) a \(B\) budeme opäť brať ako koncové body vektorov \(a=(3;1)\) a \(b=(1;2)\). Zo vzťahu, ktorý platí pre skalárny súčin dvoch vektorov, vyjadríme \(\cos\alpha\):
\[ \cos\alpha =\frac{\vec{a} \cdot \vec{b}}{\left | \vec{a} \right |\left | \vec{b} \right |}\,. \]
Po dosadení dostávame:
\[ \cos\alpha = \frac{(3;1) \cdot (1;2)}{\sqrt{3^2+1^2} \cdot \sqrt{1^2+2^2}} = \frac{3 \cdot 1 + 1 \cdot 2}{\sqrt{10} \cdot \sqrt{5}} = \frac{5}{\sqrt{50}} =\sqrt{\frac{25}{50}} = \frac{1}{\sqrt{2}}.\]
Vieme, že \(\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\) je základná hodnota goniometrickej funkcie, teda \(\alpha=45^{\circ}\), resp. hodnotu uhla \(\alpha\) môžeme vypočítať aj ako \(\arccos \frac{1}{\sqrt{2}}\). Pozorovateľ sa teda musí otočiť o uhol \(45^{\circ}\).
Ak by boli v zadaní úlohy uvedené normalizované smerové vektory, ich skalárny súčin by sa rovnal priamo \(\cos\alpha\).
\[ \cos\alpha =\frac{\vec{a}}{\left | \vec{a} \right |} \cdot \frac{\vec{b}}{\left | \vec{b} \right |} = \hat{a} \cdot \hat{b}\]
Toto je dôvod, prečo sa smery pohľadov postáv a smerové vektory medzi postavami zapisujú v zoznamoch položiek v normalizovanom tvare. Skalárny súčin môžeme s výhodou použiť aj na riešenie nasledujúceho problému. Predstavme si, že vytvárame hru, v ktorej sa hráč snaží skryť pred strážami. Bude nás teda zaujímať, či strážnik vidí alebo nevidí jednotlivých hráčov. Pre väčšiu realistickosť chceme, aby mal strážnik zorné pole, v ktorom danú postavu vidí. U človeka sa udáva veľkosť zorného uhla pre videnie oboma očami približne \(180^{\circ}\). To by bolo pre nášho strážnika priveľa, takže povedzme, že chceme, aby jeho zorný uhol bol napríklad \(170^{\circ}\).
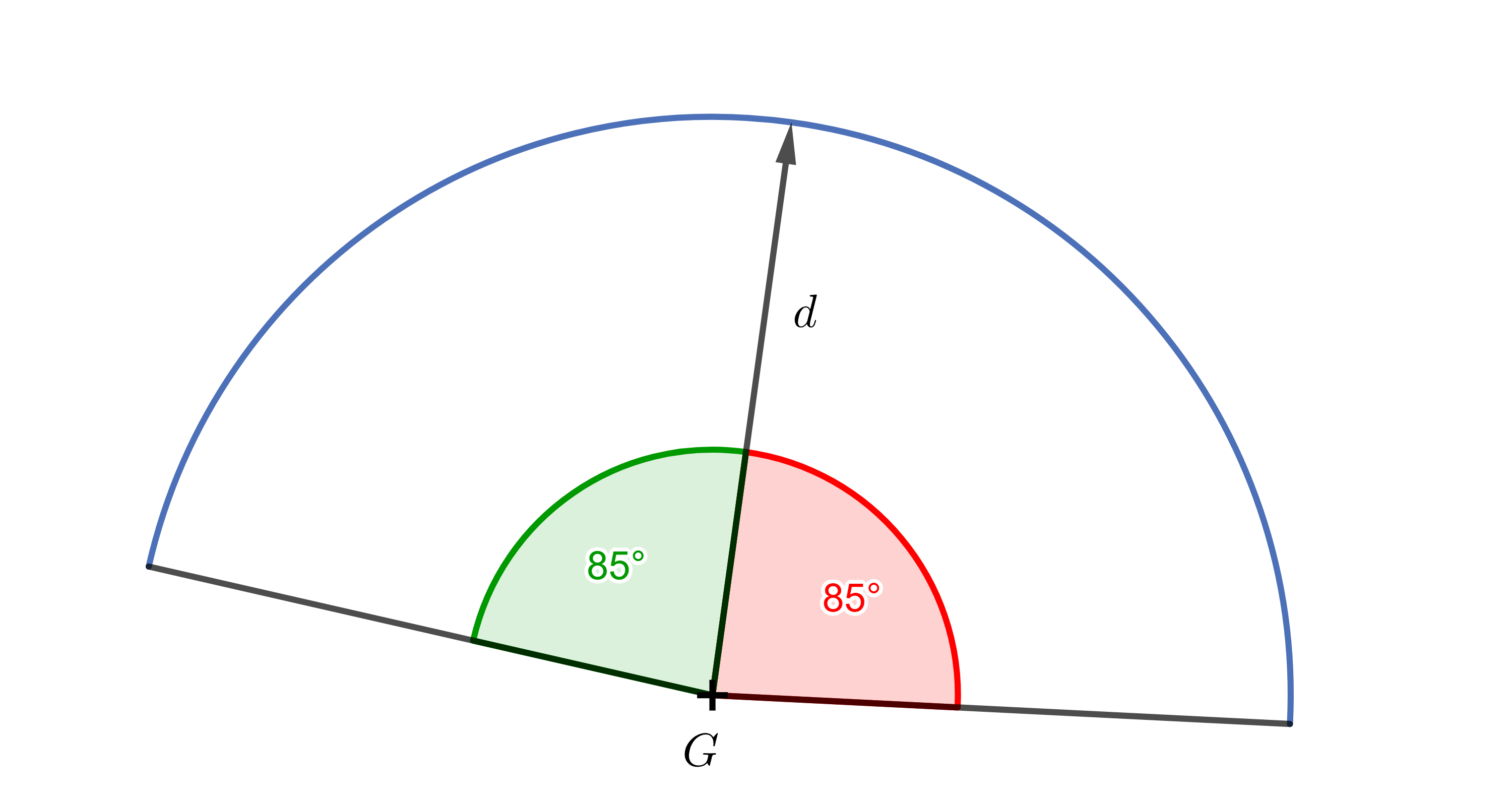
Úloha 6. Zorný uhol strážnika \(G\) je \(170^{\circ}\), Aké hodnoty budú nadobúdať skalárne súčiny medzi jeho smerom pohľadu \(\vec{d}\) a normalizovanými smerovými vektormi k objektom, ktoré strážnik vidí?
Riešenie. Od smeru pohľadu strážnika k hraniciam zorného poľa (smerom doprava aj doľava) máme \(85^{\circ}\). Stačí teda vypočítať \(\cos 85^{\circ} \dot= 0,087\). Skalárne súčiny medzi smerom pohľadu strážnika a normalizovanými smerovými vektormi k objektom, ktoré vidí, budú nadobúdať hodnoty medzi \(0,087\) a \(1\).
Do zoznamu položiek prislúchajúcich strážnikovi teda k smeru pohľadu pridáme interval, ktorý bude určovať jeho zorné pole. Pomocou neho potom môžeme kontrolovať, či strážnik hráča vidí alebo nevidí. Pre jednoduchosť predchádzajúci výsledok zaokrúhlime na jedno desatinné miesto a zorné pole strážnika teda obmedzíme hodnotou \(0,1\).
Úloha 7. Určte, či strážnik, umiestnený v počiatku súradnicovej sústavy, vidí hráča \(A=[3;-2]\), ak smer pohľadu strážnika je \(\left(\frac{1}{\sqrt{5}};\frac{2}{\sqrt{5}}\right)\) a hranica pre obmedzenie zorného poľa je daná hodnotou \(0,1\).
Riešenie. Smer pohľadu strážnika je už normalizovaný vektor. Stačí teda znormalizovať smerový vektor od strážnika k hráčovi \(A\). Keďže strážnik je v počiatku súradnicovej sústavy, stačí normalizovať vektor \(\vec{a}=(3;-2)\). Platí
\[\hat{a}=\frac{\left(3;-2\right)}{3^2+(-2)^2} = \frac{\left(3;-2\right)}{15} = \left(\frac{3}{15};\frac{-2}{15}\right).\]
Potom už môžeme vypočítať príslušný skalárny súčin týchto normalizovaných vektorov, teda:
\[\left(\frac{1}{\sqrt{5}};\frac{2}{\sqrt{5}}\right) \cdot \left(\frac{3}{\sqrt{15}};\frac{-2}{\sqrt{15}}\right) = \frac{3}{\sqrt{75}} - \frac{4}{\sqrt{75}} = -\frac{1}{\sqrt{75}} \dot= -0,12.\]
Výsledok nie je v rozmedzí od \(0,1\) do \(1\), strážnik teda hráča \(A\) nevidí. Z výsledku je navyše jasné, že medzi vektormi je väčší ako pravý uhol. Môžete sa zamyslieť, v čom sa situácia z predchádzajúceho príkladu zmení, ak strážnik nie je v počiatku súradnicovej sústavy.