Vectors
 30 min.,
30 min.,  2/3
2/3 Vectors are important not only in mathematics, but also in physics and computer science. In mathematics, they are studied within a branch called linear algebra.
A vector is usually defined as an element of an abstract mathematical structure called a vector space. A typical example of such a space is the set of all ordered n-tuples of real numbers (for instance, pairs or triples), together with the rules for adding them and multiplying them by a number. In high school mathematics, vectors are often introduced as a set of directed line segments that have the same magnitude and direction.
In physics, vectors are used to describe quantities such as the velocity and acceleration of a moving object, the forces acting on it, or electromagnetic fields. In computer science, a vector is often simply understood as an ordered list of items (not necessarily numbers). Vectors provide an efficient way of organizing and storing data, for example in machine learning applications.
However, there is also an area in computer science where vectors are used in the same way as they are defined in high school mathematics or physics. This area is the field of computer games. In fact, mastering vector operations is one of the fundamental building blocks for becoming a game programmer.
Depending on whether you are creating a 2D or 3D game, vectors have two or three coordinates and are generally used to represent geometric properties of objects within the game world. For simplicity, we will work only in two dimensions, that is, in a plane using the Cartesian coordinate system.
Note: Of course, understading vectors is just one of many fundamental building blocks. In addition to the relevant programming tools, one also needs to understand transformation matrices, such as translations, rotations, and so on. In the following tasks, we will focus only on vector operations.
Points and Direction Vectors
In the following examples, we will distinguish between points (written in square brackets) and vectors (written in round brackets). At the same time, we should keep in mind that a point \(A = [a_1; a_2]\) can also be interpreted as the endpoint of the vector \(\overrightarrow{a} = (a_1; a_2)\), whose initial point is the origin of the coordinate system.
A point has coordinates, but unlike a vector, it is not defined by magnitude and direction. The point \([0, 0]\) (or the vector \((0, 0)\)) will serve as the center of the game world.
A common use of vectors is to find the vector that describes the relationship between two objects. Let us consider a simple example with two points \(A = [a_1; a_2]\) and \(B = [b_1; b_2]\). The vector \(\overrightarrow{u}=\overrightarrow{AB}= (b_1 - a_1; b_2 - a_2)\) is usually called the direction vector. If points \(A\) and \(B\) represent characters in a game, then the vector \(\overrightarrow{AB}\) indicates the direction from one character to the other, and its magnitude represents the distance character \(A\) would have to travel to reach character \(B\).
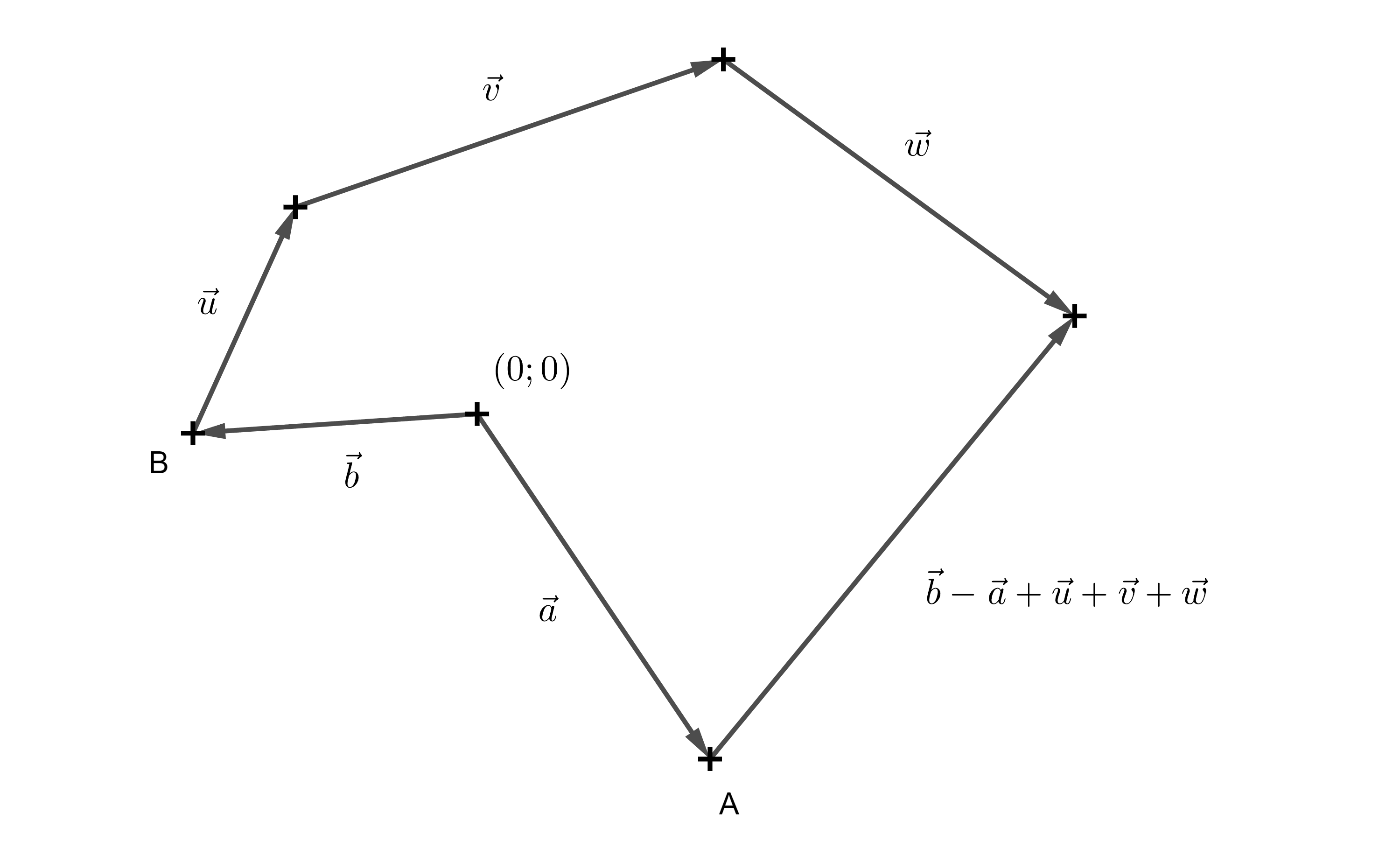
Exercise 1. In a 2D game, a programmer controls character \(A\) and a player controls character \(B\). The characters start at different locations, represented by points \(A\) and \(B\). Character \(B\) moves along a path made up of the vectors \(\overrightarrow{u}\), \(\overrightarrow{v}\), and \(\overrightarrow{w}\). Express the vector the programmer needs to determine in order for character \(A\) to shoot at character \(B\).
Solution. It is clear that character \(B\) has moved along the path \(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}\). However, characters \(A\) and \(B\) started at different positions. So, we still need to determine the vector that starts at point \(A\) and ends at point \(B\) — that is, the direction vector \(\overrightarrow{AB}\). We know that point \(A\) can be understood as the endpoint of the vector \(\overrightarrow{a}\), and point \(B\) as the endpoint of the vector \(\overrightarrow{b}\). Then the vector \(\overrightarrow{AB} = \overrightarrow{b}-\overrightarrow{a}\) (since points and corresponding vectors share the same coordinates, the notation \(\overrightarrow{AB} = B-A\) is also commonly used). Therefore, the vector needed for character \(A\) to shoot at character \(B\) is \(\overrightarrow{b}-\overrightarrow{a}+\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}\).
Each character in the game world is also associated with a vector in the sense of a list of items — such as the character’s name, role, and position. Another important property of every character is the direction they are facing. This direction is represented by a so-called normalized direction vector, which is a direction vector with a magnitude of \(1\).
Normalized direction vectors are also used to store information about the directions in which other characters or objects are located.
Note: The reason why normalized versions of direction vectors are used in game worlds will be explained later.
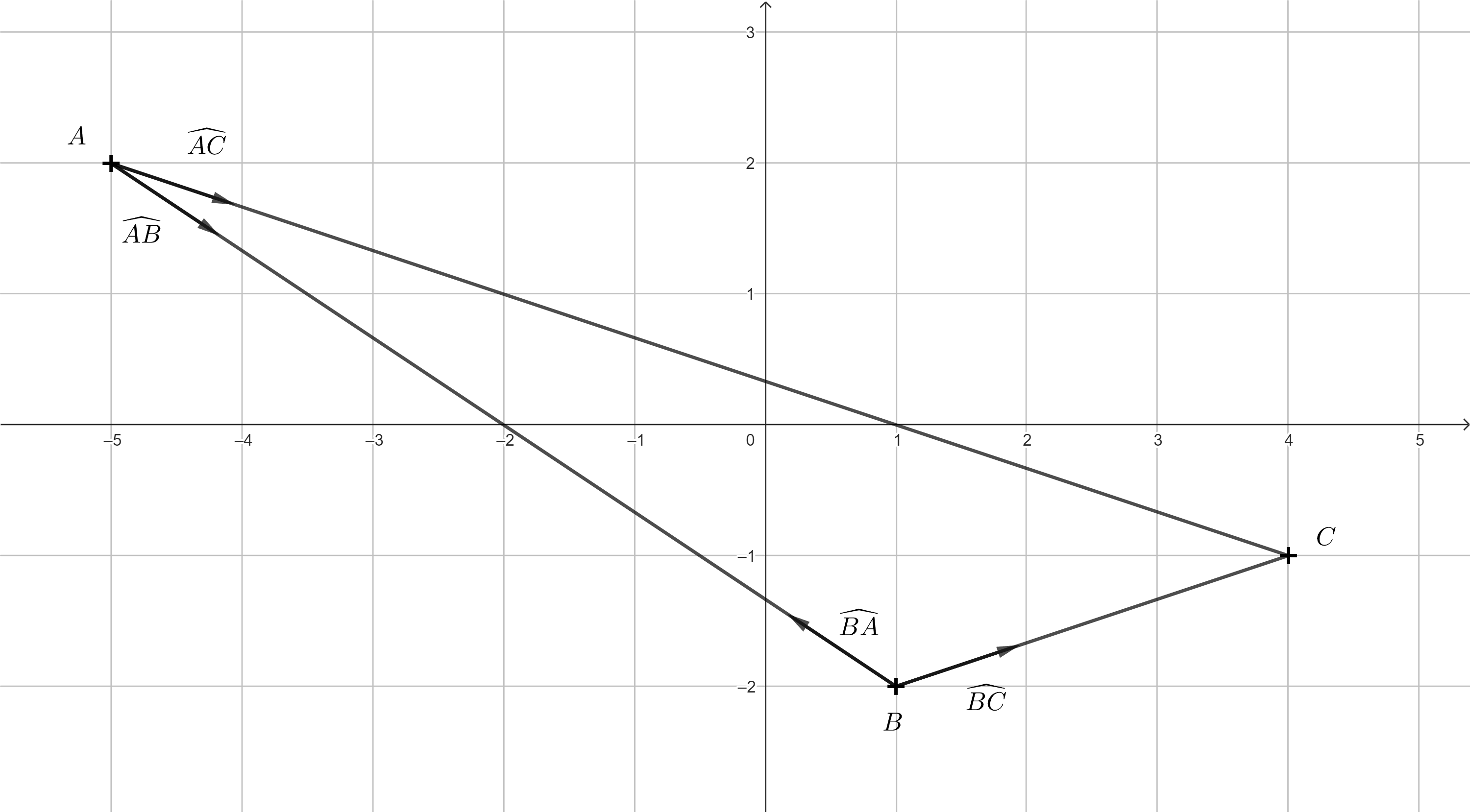
Exercise 2. Let the characters be given by the points \(A = [-5; 2]\), \(B = [1; -2]\), and \(C = [4; -1]\). Determine the normalized direction vectors from characters \(A\) and \(B\) pointing toward the other characters. Draw a corresponding diagram.
Solution. For the direction vector \(\overrightarrow{AB}\), we have: \(\overrightarrow{AB}= (1-(-5); -2-2) = (6;-4)\). To normalize this vector, we simply divide it by its magnitude: \(\left | \overrightarrow{AB} \right | = \sqrt{6^2+(-2)^2} = \sqrt{52}.\) The normalized vector corresponding to \(\overrightarrow{AB}\) is denoted by \(\widehat{AB}\), and we get:
\[ \widehat{AB} = \frac{\overrightarrow{AB}}{\left | \overrightarrow{AB} \right | } = \frac{(6;-4)}{\sqrt{52}} = \left(\frac{3}{\sqrt{13}};-\frac{2}{\sqrt{13}}\right). \]
Similarly
\[ \widehat{AC} = \frac{\overrightarrow{AC}}{\left | \overrightarrow{AC} \right | } = \frac{(9;-3)}{\sqrt{90}} = \left(\frac{3}{\sqrt{10}};-\frac{1}{\sqrt{10}}\right), \]
\[\widehat{BC} = \frac{\overrightarrow{BC}}{\left | \overrightarrow{BC} \right | } = \frac{(3;1)}{\sqrt{10}} = \left(\frac{3}{\sqrt{10}};\frac{1}{\sqrt{10}}\right),\]
\[\widehat{BA} = \frac{\overrightarrow{BA}}{\left | \overrightarrow{BA} \right | } = \frac{(-6;4)}{\sqrt{52}} = \left(-\frac{3}{\sqrt{13}};\frac{2}{\sqrt{13}}\right).\]
There was no need to calculate the vector \(\widehat{BA}\), since it has the same magnitude as \(\widehat{AB}\) but points in the opposite direction. The coordinates of such vectors differ only in sign.
Exercise 3. Let the positions of characters \(A = [a_1;a_2]\) and \(B = [b_1;b_2]\) be given, with the characters standing at different locations. Determine:
the normalized direction vector \(\widehat{BA}\),
where character \(B\) will be located after walking three unit lengths in the direction of character \(A\)?
Solution. a) What we calculated in the previous example using specific coordinates can now be written in general form. That is,
\[\widehat{BA} = \frac{\overrightarrow{BA}}{\left| \overrightarrow{BA} \right| } = \frac{(a_1-b_1;a_2-b_2)}{\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}}.\]
- From the previous step, we already have a unit-length direction vector. Now we simply multiply it by 3 and add it to the position of character \(B\). We get:
\[B+3\cdot\widehat{BA} = [b_1;b_2] +3\frac{(a_1-b_1;a_2-b_2)}{\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}}.\]
The Dot Product and Its Applications
The result of the dot product of two vectors is a scalar — that is, a real number. In game programming, the dot product of normalized vectors plays an important role.
Exercise 4. Determine the dot products of the normalized direction vectors from the solution to Exercise 2.
Solution.
\[ \widehat{AB} \cdot \widehat{AC} = \left(\frac{3}{\sqrt{13}};-\frac{2}{\sqrt{13}}\right) \cdot \left(\frac{3}{\sqrt{10}};-\frac{1}{\sqrt{10}}\right) = \frac{9}{\sqrt{130}}+\frac{2}{\sqrt{130}} = \frac{11}{\sqrt{130}} \dot=0{.}96 \]
\[ \widehat{BA} \cdot \widehat{BC} = \left(-\frac{3}{\sqrt{13}};\frac{2}{\sqrt{13}}\right) \cdot \left(\frac{3}{\sqrt{10}};\frac{1}{\sqrt{10}}\right) = -\frac{9}{\sqrt{130}}+\frac{2}{\sqrt{130}} = -\frac{7}{\sqrt{130}} \dot= -0{.}054 \]
The dot product of two normalized vectors is very useful, because it tells us to what extent the two vectors point in the same or similar direction! In this case, the value of the dot product ranges from \(-1\) to \(1\): a value of \(1\) means the vectors point in exactly the same direction, a value of \(-1\) means they point in exactly opposite directions, and a value close to \(0\) means the vectors are nearly perpendicular to each other. The reason for this range from \(-1\) to \(1\) is that we are working within the range of values of the cosine function. For any two vectors \(\vec{p}\), \(\vec{q}\) the dot product can also be written as:
\[ \vec{p} \cdot \vec{q}=\left | \vec{p} \right |\left | \vec{q} \right |\cos\alpha, \]
where \(\alpha\) is the angle between vectors \(\vec{p}\) and \(\vec{q}\).
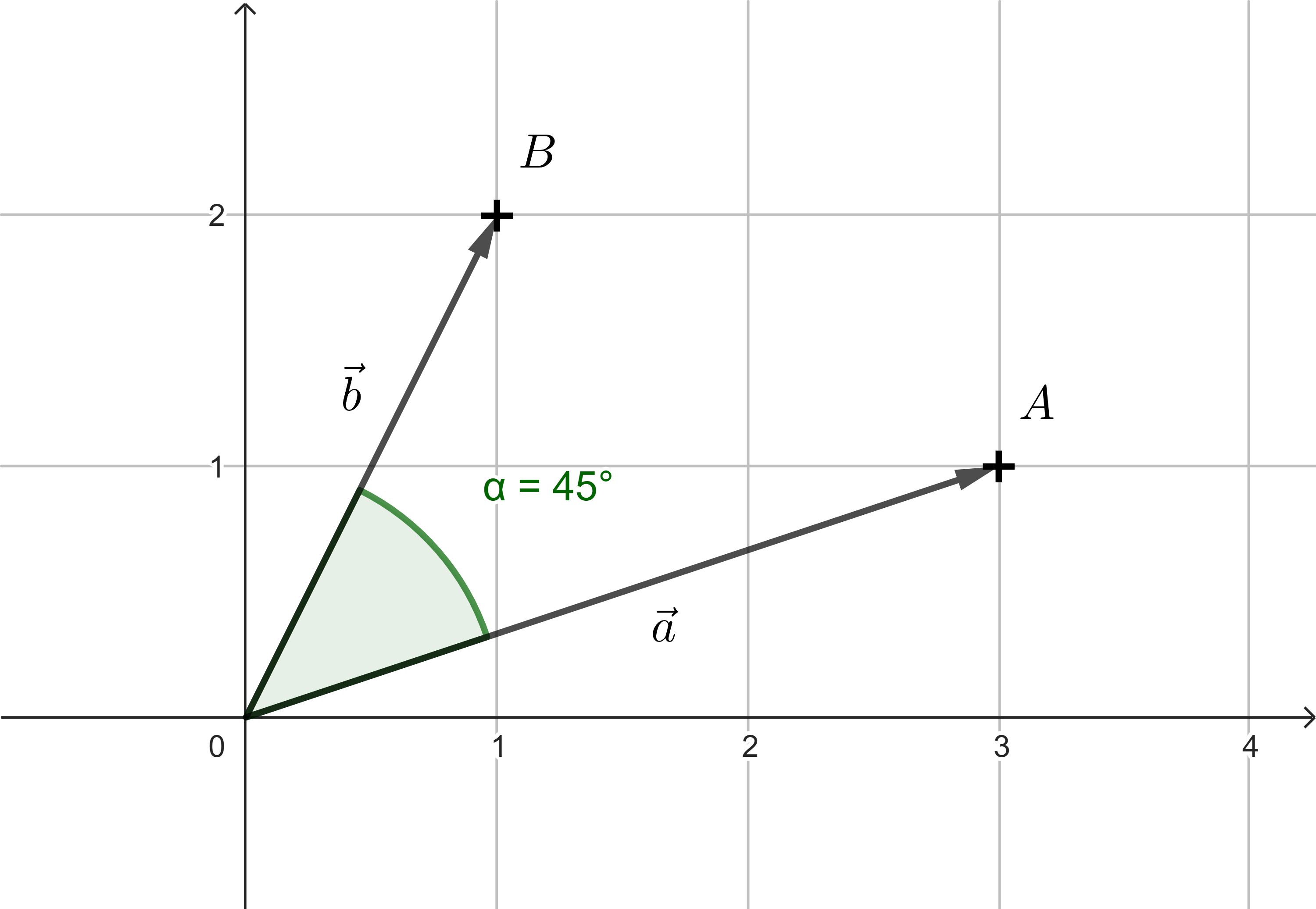
Exercise 5. An observer at the origin is looking at object \(A=[3;1]\). Determine the angle \(\alpha\) by which the observer must rotate so that they are facing directly toward object \(B=[1;2]\).
Solution. We again treat points \(A\) and \(B\) as the endpoints of vectors \(\vec{a}=(3;1)\) and \(\vec{b}=(1;2)\). From the formula for the dot product of two vectors, we can express \(\cos\alpha\):
\[ \cos\alpha =\frac{\vec{a} \cdot \vec{b}}{\left | \vec{a} \right |\left | \vec{b} \right |}\,. \]
After substituting the specific values, we obtain
\[ \cos\alpha = \frac{(3;1) \cdot (1;2)}{\sqrt{3^2+1^2} \cdot \sqrt{1^2+2^2}} = \frac{3 \cdot 1 + 1 \cdot 2}{\sqrt{10} \cdot \sqrt{5}} = \frac{5}{\sqrt{50}} =\sqrt{\frac{25}{50}} = \frac{1}{\sqrt{2}}.\]
We know that \(\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\) is a well-known trigonometric value, which means that \(\alpha=45^{\circ}\). Alternatively, we can calculate the angle \(\alpha\) as \(\arccos \frac{1}{\sqrt{2}}\). Therefore, the observer must rotate by an angle of \(45^{\circ}\).
If the normalized direction vectors were explicitly given in the problem, then their dot product would be equal to \(\cos\alpha\).
\[ \cos\alpha =\frac{\vec{a}}{\left | \vec{a} \right |} \cdot \frac{\vec{b}}{\left | \vec{b} \right |} = \hat{a} \cdot \hat{b}\]
This is the reason why characters’ facing directions and the direction vectors between characters are typically stored in normalized form in attribute lists.
The dot product can also be conveniently used to solve the following problem. Let’s say I am designing a game where the player is trying to hide from guards. In that case, we are interested in whether or not a guard can see individual players.
To make the game more realistic, we want the guard to have a field of view within which a player is visible. For humans, the horizontal visual field covered by both eyes is approximately \(180^{\circ}\), but that would be too wide for our guard. So let’s say we want the guard’s field of view to be \(170^{\circ}\).
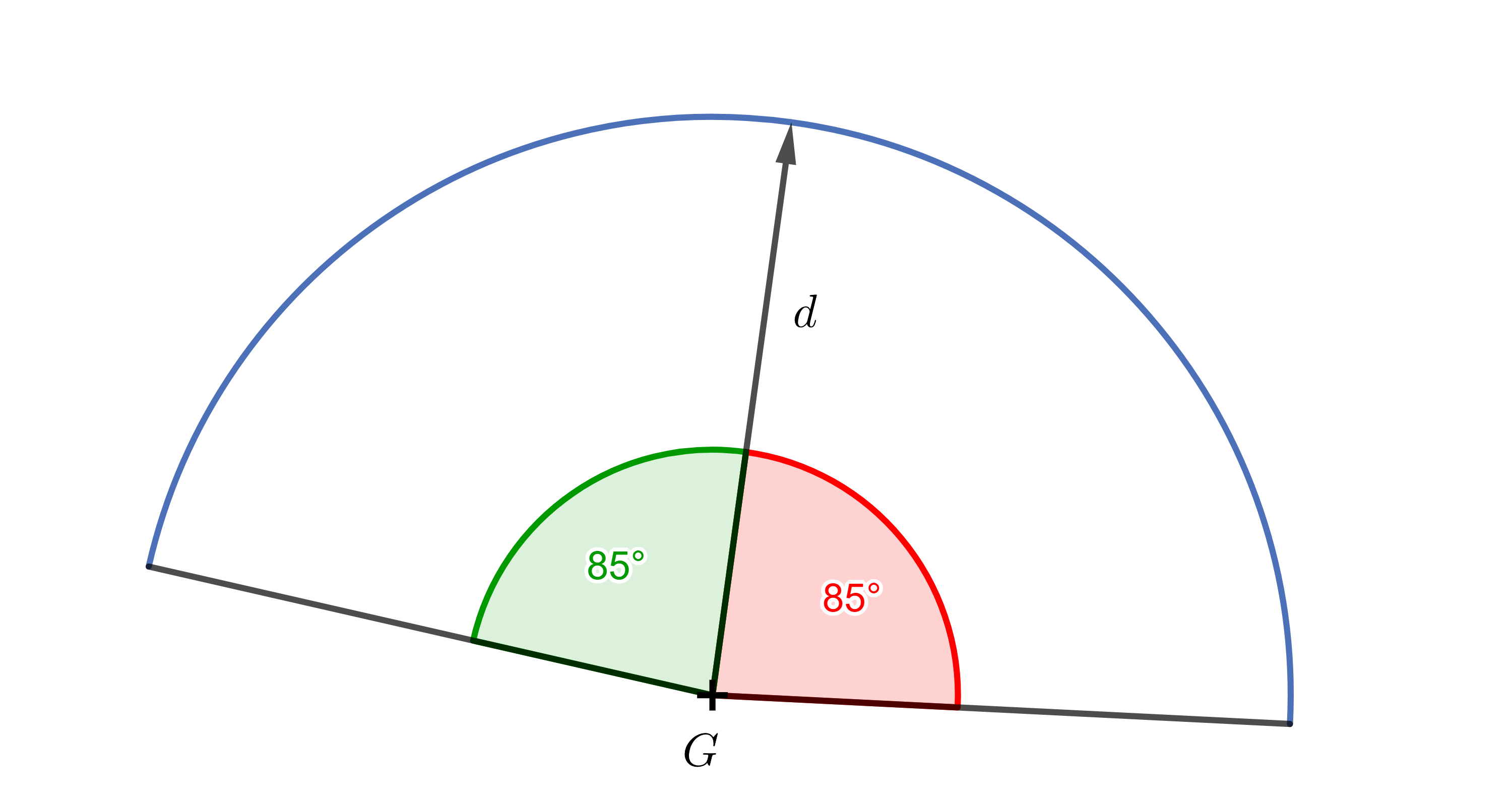
Exercise 6. The guard \(G\) has a field of view of \(170^{\circ}\). What will be the values of the dot products between the guard’s viewing direction \(\vec{d}\) and the normalized direction vectors to the objects that the guard can see?
Solution. From the guard’s viewing direction to the boundaries of their field of view — both to the left and right — the angle is \(85^{\circ}\). We just need to calculate \(\cos 85^{\circ} \dot= 0{.}087\). So, the dot products between the guard’s viewing direction and the normalized direction vectors to visible objects will fall within the range from approximately \(0{.}087\) to \(1\).
In the attribute list associated with the guard, we add not only their viewing direction, but also a threshold that defines their field of view. Using this threshold, we can check whether or not the guard sees a given player. For simplicity, we round the previous result to one decimal place and limit the guard’s field of view using a threshold value of \(0{.}1\).
Exercise 7. Determine whether a guard located at the origin can see player \(A=[3;-2]\), given that the guard’s viewing direction is \(\left(\frac{1}{\sqrt{5}};\frac{2}{\sqrt{5}}\right)\) and the threshold for the guard’s field of view is set to \(0{.}1\).
Solution. The guard’s viewing direction is already a normalized vector. So we just need to normalize the direction vector from the guard to player \(A\). Since the guard is located at the origin, this is equivalent to normalizing the vector \(\vec{a}=(3;-2)\). We get:
\[ \hat{a}=\frac{\left(3;-2\right)}{3^2+(-2)^2} = \frac{\left(3;-2\right)}{15} = \left(\frac{3}{15};\frac{-2}{15}\right). \]
Now we calculate the dot product of the two normalized vectors:
\[ \left(\frac{1}{\sqrt{5}};\frac{2}{\sqrt{5}}\right) \cdot \left(\frac{3}{\sqrt{15}};\frac{-2}{\sqrt{15}}\right) = \frac{3}{\sqrt{75}} - \frac{4}{\sqrt{75}} = -\frac{1}{\sqrt{75}} \dot= -0{.}12. \]
Since the result is not in the range between \(0,1\) and \(1\), the guard does not see player \(A\). Moreover, the negative result indicates that the angle between the vectors is greater than a right angle.
Think about how would the situation change if the guard was not positioned at the origin.