Wektory
 30 min.,
30 min.,  2/3
2/3 Wektory są ważne nie tylko w matematyce, ale także w fizyce i informatyce. W matematyce są one badane w ramach gałęzi zwanej algebrą liniową.
Wektor jest zwykle definiowany jako element abstrakcyjnej struktury matematycznej zwanej przestrzenią wektorową. Typowym przykładem takiej przestrzeni jest zbiór wszystkich uporządkowanych n-krotności liczb rzeczywistych (na przykład par lub trójek), wraz z regułami ich dodawania i mnożenia przez liczbę. W matematyce w szkole średniej, wektory są często przedstawiane jako zbiór skierowanych odcinków linii, które mają tę samą wielkość i kierunek.
W fizyce wektory są używane do opisywania takich wielkości jak prędkość i przyspieszenie poruszającego się obiektu, działające na niego siły lub pola elektromagnetyczne. W informatyce wektor jest często rozumiany po prostu jako uporządkowana lista elementów (niekoniecznie liczb). Wektory zapewniają efektywny sposób organizowania i przechowywania danych, na przykład w aplikacjach uczenia maszynowego.
Istnieje jednak również dziedzina informatyki, w której wektory są używane w taki sam sposób, w jaki są definiowane w matematyce lub fizyce w szkole średniej. Obszarem tym są gry komputerowe. W rzeczywistości, opanowanie operacji wektorowych jest jednym z podstawowych elementów niezbędnych do zostania programistą gier.
W zależności od tego, czy tworzysz grę 2D czy 3D, wektory mają dwie lub trzy współrzędne i są zwykle używane do reprezentowania geometrycznych właściwości obiektów w świecie gry. Dla uproszczenia będziemy pracować tylko w dwóch wymiarach, to znaczy na płaszczyźnie przy użyciu kartezjańskiego układu współrzędnych.
Uwaga: Oczywiście zrozumienie wektorów jest tylko jednym z wielu podstawowych elementów. Oprócz odpowiednich narzędzi programistycznych, należy również zrozumieć macierze transformacji, takie jak translacje, obroty i tak dalej. W poniższych zadaniach skupimy się tylko na operacjach wektorowych.
Punkty i kierunek wektora
W poniższych przykładach będziemy rozróżniać punkty (zapisane w nawiasach kwadratowych) i wektory (zapisane w nawiasach okrągłych). Jednocześnie należy pamiętać, że punkt \(A = [a_1; a_2]\) może być również interpretowany jako punkt końcowy wektora \(\overrightarrow{a} = (a_1; a_2)\), którego punktem początkowym jest początek układu współrzędnych.
Punkt ma współrzędne, ale w przeciwieństwie do wektora, nie jest zdefiniowany przez wielkość i kierunek. Punkt \([0, 0]\) (lub wektor \((0, 0)\)) będzie służył jako środek świata gry.
Powszechnym zastosowaniem wektorów jest znalezienie wektora opisującego relację między dwoma obiektami. Rozważmy prosty przykład z dwoma punktami \(A = [a_1;a_2]\) i \(B = [b_1; b_2]\). Wektor \(\overrightarrow{u}=\overrightarrow{AB}= (b_1 - a_1; b_2 - a_2)\) jest zwykle nazywany wektorem kierunku. Jeśli punkty \(A\) i \(B\) reprezentują postacie w grze, to wektor \(\overrightarrow{AB}\) wskazuje kierunek od jednej postaci do drugiej, a jego wielkość reprezentuje odległość, jaką musiałby pokonać znak \(A\), aby dotrzeć do znaku \(B\).
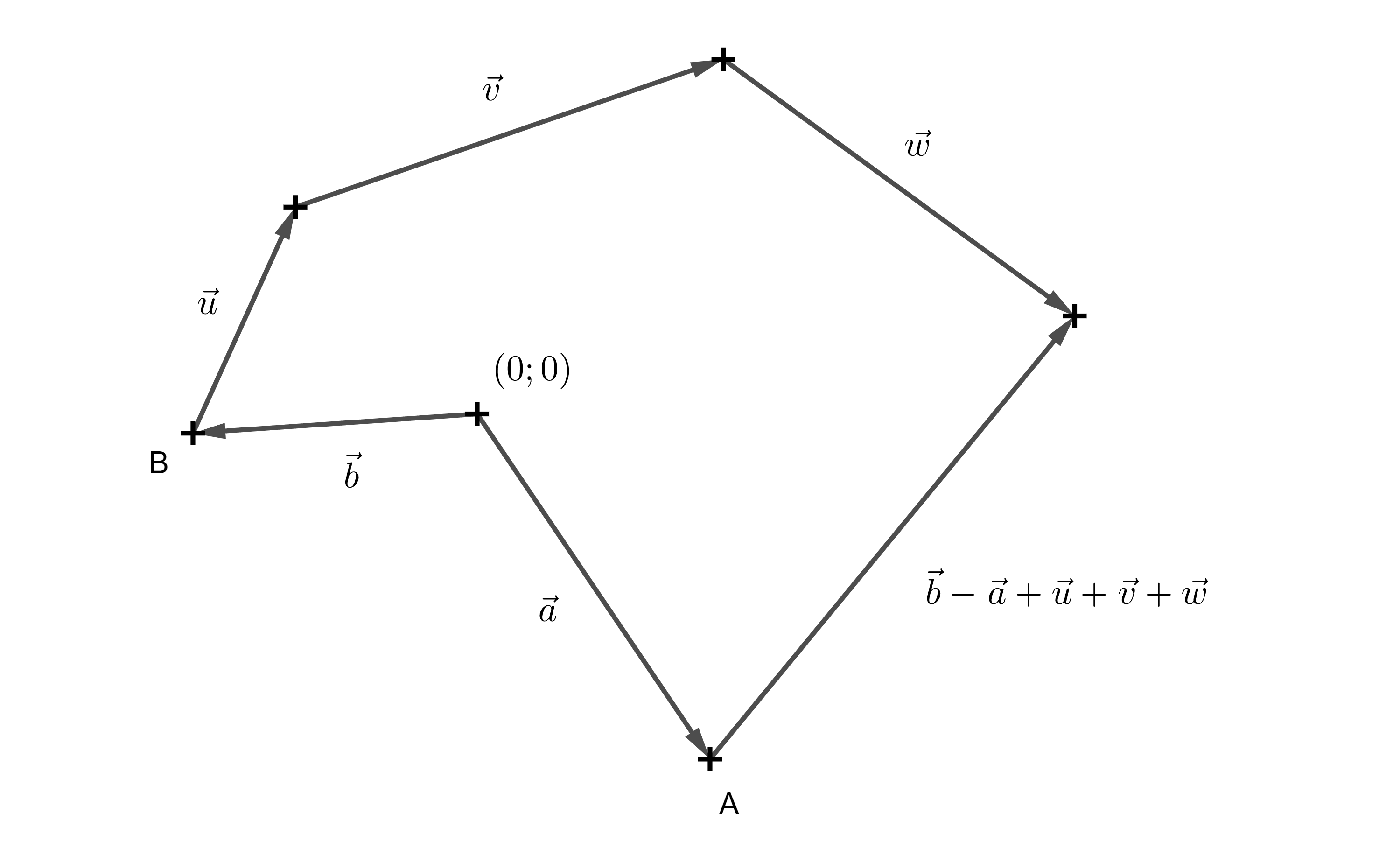
Zadanie 1. W grze 2D programista steruje postacią \(A\), a gracz postacią \(B\). Postacie zaczynają w różnych miejscach, reprezentowanych przez punkty \(A\) i \(B\). Postać \(B\) porusza się po ścieżce złożonej z wektorów \(\overrightarrow{u}\), \(\overrightarrow{v}\) i \(\overrightarrow{w}\). Wyraź wektor, który programista musi określić, aby postać \(A\) strzeliła do postaci \(B\).
Rozwiązanie. Jest oczywiste, że znak \(B\) poruszył się po ścieżce \(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}\). Jednak znaki \(A\) i \(B\) rozpoczęły się na różnych pozycjach. Nadal musimy więc określić wektor, który zaczyna się w punkcie \(A\) i kończy w punkcie \(B\) - czyli wektor kierunku \(\overrightarrow{AB}\). We know that point \(A\) can be understood as the endpoint of the vector \(\overrightarrow{a}\), and point \(B\) as the endpoint of the vector \(\overrightarrow{b}\). Wtedy wektor \(\overrightarrow{AB} = \overrightarrow{b}-\overrightarrow{a}\) (ponieważ punkty i odpowiadające im wektory mają te same współrzędne, notacja \(\overrightarrow{AB} = B-A\) jest również powszechnie używana). Dlatego wektor potrzebny do tego, by postać \(A\) strzeliła do postaci \(B\) wynosi \(\overrightarrow{b}-\overrightarrow{a}+\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}\).
Każda postać w świecie gry jest również powiązana z wektorem w sensie listy elementów - takich jak imię, rola i pozycja postaci. Kolejną ważną właściwością każdej postaci jest kierunek, w którym jest zwrócona. Kierunek ten jest reprezentowany przez tak zwany znormalizowany wektor kierunku, który jest wektorem kierunku o wielkości \(1\).
Znormalizowane wektory kierunku są również używane do przechowywania informacji o kierunkach, w których znajdują się inne postacie lub obiekty.
Uwaga: Powód, dla którego znormalizowane wersje wektorów kierunku są używane w światach gier, zostanie wyjaśniony później.
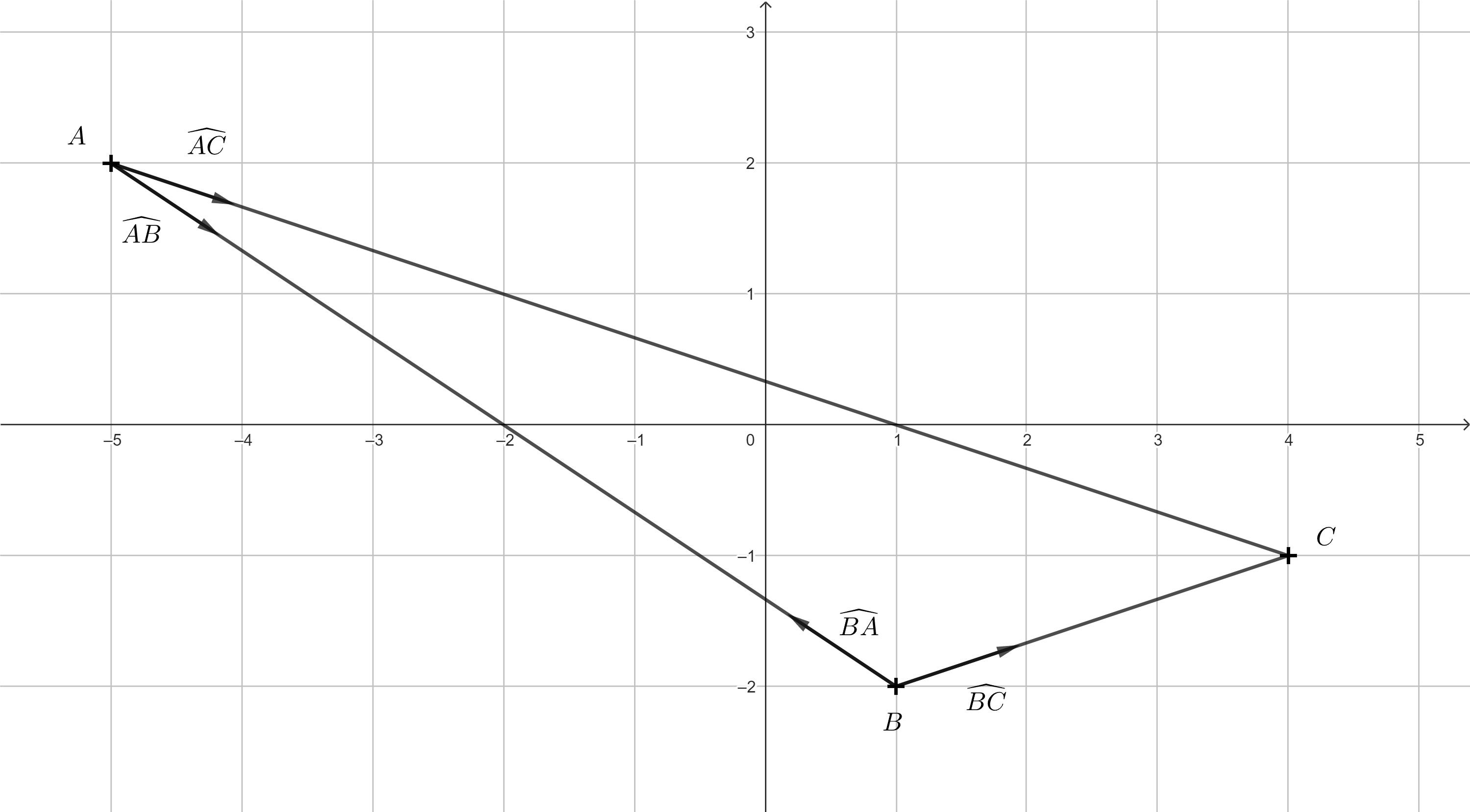
Zadanie 2. Niech znakami będą punkty \(A = [-5; 2]\), \(B = [1; -2]\) i \(C = [4; -1]\). Wyznacz znormalizowane wektory kierunku od znaków \(A\) i \(B\) skierowane w stronę innych znaków. Narysuj odpowiedni diagram.
Rozwiązanie. Dla wektora o kierunku \(\overrightarrow{AB}\) mamy: \(\overrightarrow{AB}= (1-(-5); -2-2) = (6;-4)\). Aby znormalizować ten wektor, po prostu dzielimy go przez jego wielkość: \(\left | \overrightarrow{AB} \right | = \sqrt{6^2+(-2)^2} = \sqrt{52}.\) Znormalizowany wektor odpowiadający \(\overrightarrow{AB}\) jest oznaczany przez \(\widehat{AB}\) i otrzymujemy:
\[ \widehat{AB} = \frac{\overrightarrow{AB}}{\left | \overrightarrow{AB} \right | } = \frac{(6;-4)}{\sqrt{52}} = \left(\frac{3}{\sqrt{13}};-\frac{2}{\sqrt{13}}\right). \]
Podobnie
\[ \widehat{AC} = \frac{\overrightarrow{AC}}{\left | \overrightarrow{AC} \right | } = \frac{(9;-3)}{\sqrt{90}} = \left(\frac{3}{\sqrt{10}};-\frac{1}{\sqrt{10}}\right), \]
\[\widehat{BC} = \frac{\overrightarrow{BC}}{\left | \overrightarrow{BC} \right | } = \frac{(3;1)}{\sqrt{10}} = \left(\frac{3}{\sqrt{10}};\frac{1}{\sqrt{10}}\right),\]
\[\widehat{BA} = \frac{\overrightarrow{BA}}{\left | \overrightarrow{BA} \right | } = \frac{(-6;4)}{\sqrt{52}} = \left(-\frac{3}{\sqrt{13}};\frac{2}{\sqrt{13}}\right).\]
Nie było potrzeby obliczania wektora \(\widehat{BA}\), ponieważ ma on taką samą wielkość jak \(\widehat{AB}\), ale jest skierowany w przeciwnym kierunku. Współrzędne takich wektorów różnią się tylko znakiem.
Zadanie 3. Dane są pozycje znaków \(A = [a_1;a_2]\) i \(B = [b_1;b_2]\), przy czym znaki te stoją w różnych miejscach. Wyznaczyć:
znormalizowany wektor kierunku \(\widehat{BA}\),
gdzie znajdzie się znak \(B\) po przejściu trzech jednostek długości w kierunku znaku \(A\)?
Rozwiązanie. a) To, co obliczyliśmy w poprzednim przykładzie przy użyciu konkretnych współrzędnych, można teraz zapisać w formie ogólnej. To znaczy,
\[\widehat{BA} = \frac{\overrightarrow{BA}}{\left| \overrightarrow{BA} \right| } = \frac{(a_1-b_1;a_2-b_2)}{\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}}.\]
- Z poprzedniego kroku mamy już wektor kierunku o jednostkowej długości. Teraz po prostu mnożymy go przez 3 i dodajemy do pozycji znaku \(B\). Otrzymujemy:
\[B+3\cdot\widehat{BA} = [b_1;b_2] +3\frac{(a_1-b_1;a_2-b_2)}{\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}}.\]
Iloczyn skalarny i jego zastosowania
Wynikiem iloczynu skalarnego dwóch wektorów jest skalar, czyli liczba rzeczywista. W programowaniu gier iloczyn skalarny znormalizowanych wektorów odgrywa ważną rolę.
Zadanie 4. Wyznacz iloczyn skalarny znormalizowanych wektorów kierunku z rozwiązania ćwiczenia 2.
Rozwiązanie.
\[ \widehat{AB} \cdot \widehat{AC} = \left(\frac{3}{\sqrt{13}};-\frac{2}{\sqrt{13}}\right) \cdot \left(\frac{3}{\sqrt{10}};-\frac{1}{\sqrt{10}}\right) = \frac{9}{\sqrt{130}}+\frac{2}{\sqrt{130}} = \frac{11}{\sqrt{130}} \dot=0{,}96 \]
\[ \widehat{BA} \cdot \widehat{BC} = \left(-\frac{3}{\sqrt{13}};\frac{2}{\sqrt{13}}\right) \cdot \left(\frac{3}{\sqrt{10}};\frac{1}{\sqrt{10}}\right) = -\frac{9}{\sqrt{130}}+\frac{2}{\sqrt{130}} = -\frac{7}{\sqrt{130}} \dot= -0{,}054 \]
Iloczyn skalarny dwóch znormalizowanych wektorów jest bardzo przydatny, ponieważ mówi nam, w jakim stopniu dwa wektory są skierowane w tym samym lub podobnym kierunku! W tym przypadku wartość iloczynu skalarnego waha się od \(-1\) do \(1\): wartość \(1\) oznacza, że wektory są skierowane dokładnie w tym samym kierunku, wartość \(-1\) oznacza, że są skierowane dokładnie w przeciwnych kierunkach, a wartość bliska \(0\) oznacza, że wektory są prawie prostopadłe do siebie. Powodem tego zakresu od \(-1\) do \(1\) jest to, że pracujemy w zakresie wartości funkcji cosinus. Dla dowolnych dwóch wektorów \(\vec{p}\), \(\vec{q}\) iloczyn skalarny można również zapisać jako:
\[ \vec{p} \cdot \vec{q}=\left | \vec{p} \right |\left | \vec{q} \right |\cos\alpha, \]
gdzie \(\alpha\) jest kątem pomiędzy wektorami \(\vec{p}\) i \(\vec{q}\).
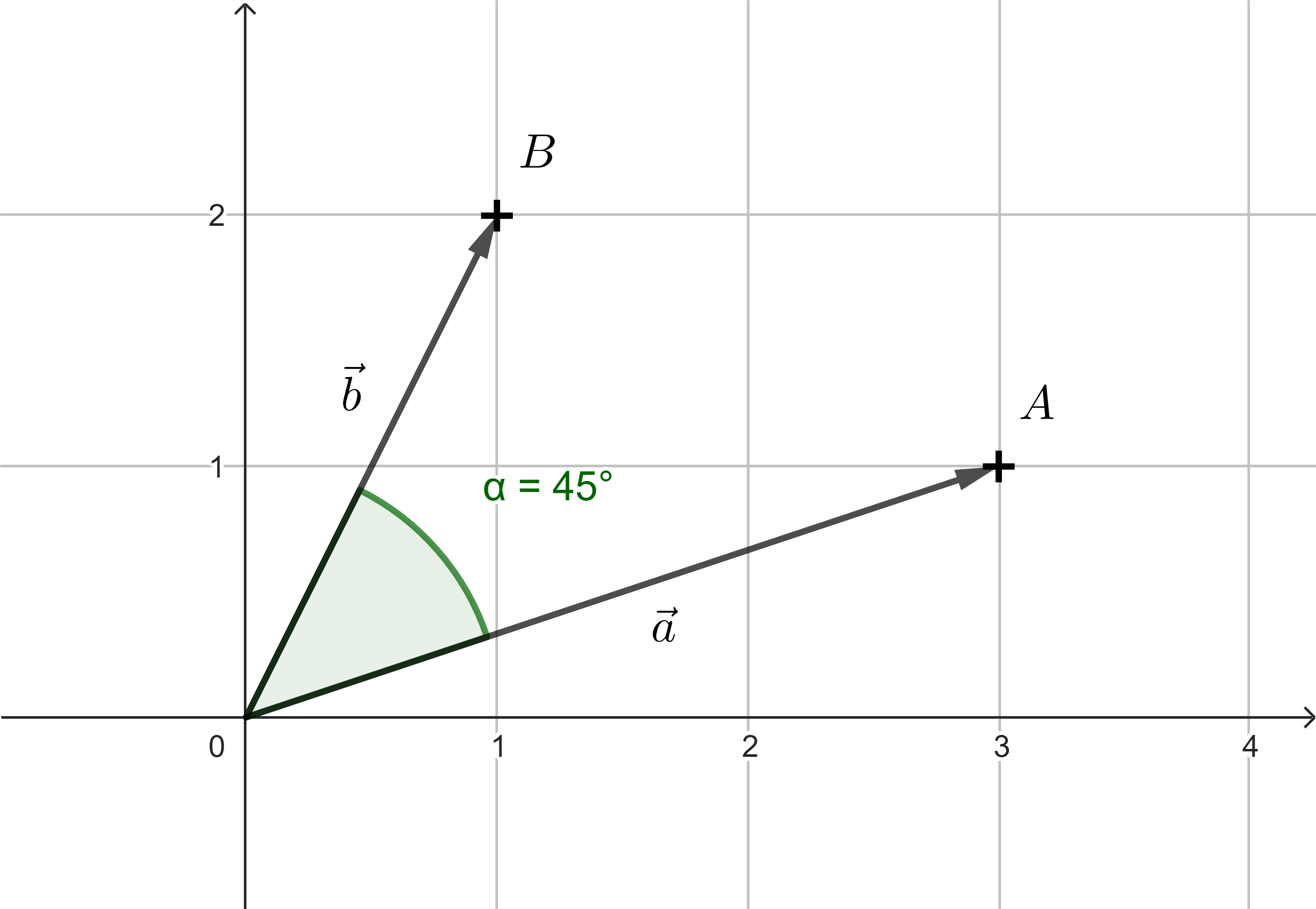
Zadanie 5. Obserwator znajdujący się w punkcie początkowym patrzy na obiekt \(A=[3;1]\). Określić kąt \(\alpha\), o który obserwator musi się obrócić, aby znaleźć się bezpośrednio w kierunku obiektu. \(B=[1;2]\).
Rozwiązanie. Ponownie traktujemy punkty \(A\) i \(B\) jako punkty końcowe wektorów \(\vec{a}=(3;1)\) i \(\vec{b}=(1;2)\). Na podstawie wzoru na iloczyn skalarny dwóch wektorów możemy wyrazić \(\cos\alpha\):
\[ \cos\alpha =\frac{\vec{a} \cdot \vec{b}}{\left | \vec{a} \right |\left | \vec{b} \right |}\,. \]
Po podstawieniu określonych wartości otrzymujemy
\[ \cos\alpha = \frac{(3;1) \cdot (1;2)}{\sqrt{3^2+1^2} \cdot \sqrt{1^2+2^2}} = \frac{3 \cdot 1 + 1 \cdot 2}{\sqrt{10} \cdot \sqrt{5}} = \frac{5}{\sqrt{50}} =\sqrt{\frac{25}{50}} = \frac{1}{\sqrt{2}}.\]
Wiemy, że \(\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\) jest dobrze znaną wartością trygonometryczną, co oznacza, że \(\alpha=45^{\circ}\). Alternatywnie, możemy obliczyć kąt \(\alpha\) jako \(\arccos \frac{1}{\sqrt{2}}\). Dlatego obserwator musi obrócić się o kąt \(45^{\circ}\).
Gdyby znormalizowane wektory kierunku były jawnie podane w problemie, to ich iloczyn skalarny byłby równy \(\cos\alpha\).
\[ \cos\alpha =\frac{\vec{a}}{\left | \vec{a} \right |} \cdot \frac{\vec{b}}{\left | \vec{b} \right |} = \hat{a} \cdot \hat{b}\]
Jest to powód, dla którego kierunki znaków i wektory kierunków między znakami są zwykle przechowywane w znormalizowanej formie na listach atrybutów.
Iloczyn skalarny może być również wygodnie wykorzystany do rozwiązania następującego zadania. Powiedzmy, że projektuję grę, w której gracz próbuje ukryć się przed strażnikami. W takim przypadku interesuje nas, czy strażnik widzi poszczególnych graczy.
Aby gra była bardziej realistyczna, chcemy, aby strażnik miał pole widzenia, w którym gracz jest widoczny. W przypadku ludzi poziome pole widzenia obejmowane przez oboje oczu wynosi w przybliżeniu \(180^{\circ}\), ale byłoby to zbyt szerokie dla naszego strażnika. Powiedzmy więc, że pole widzenia strażnika powinno wynosić \(170^{\circ}\).
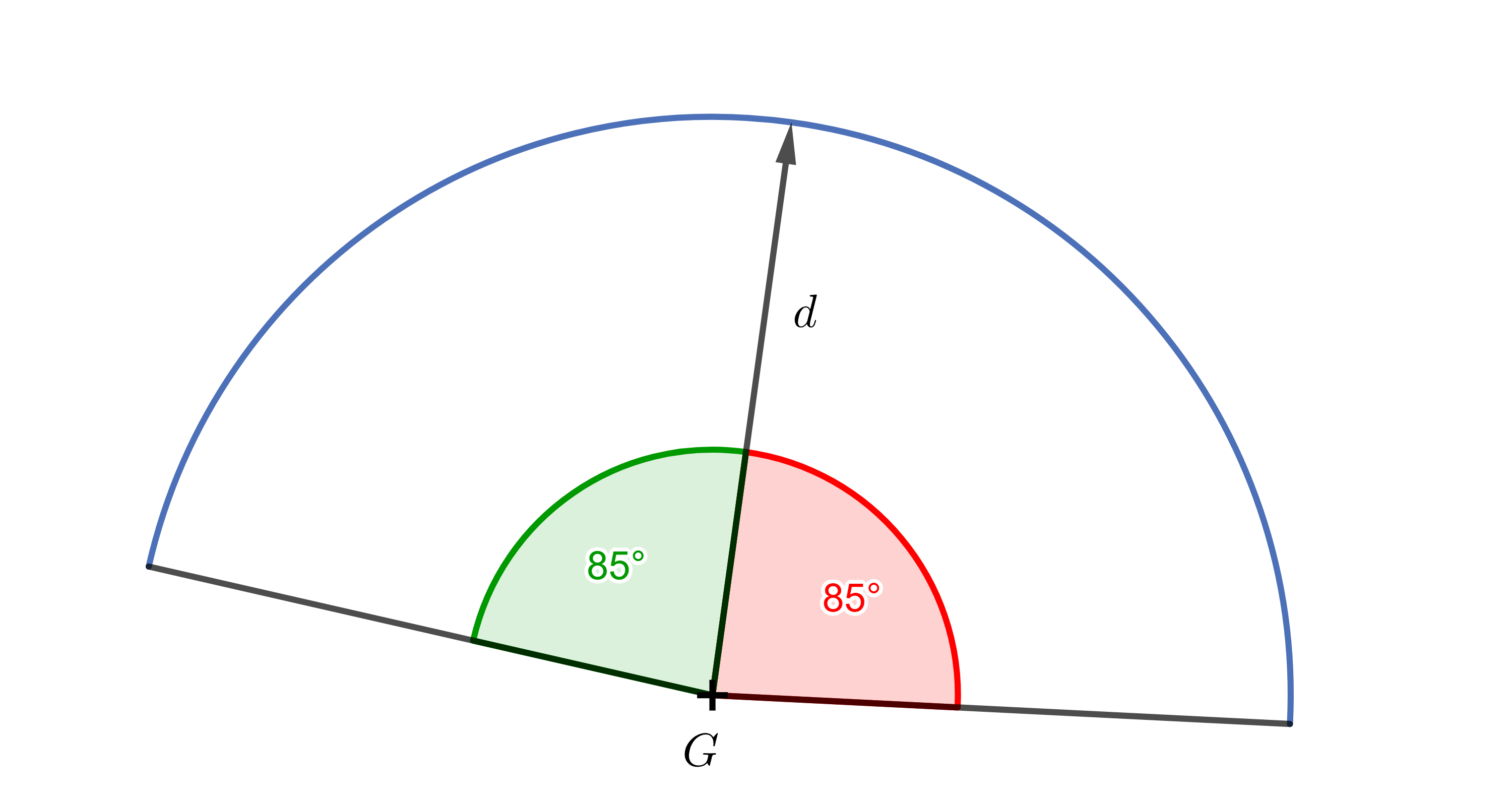
Zadanie 6. Osłona \(G\) ma pole widzenia wynoszące \(170^{\circ}\). Jakie będą wartości iloczynów punktowych między kierunkiem patrzenia strażnika \(\vec{d}\) i znormalizowane wektory kierunku do obiektów, które widzi strażnik?
Rozwiązanie. Od kierunku patrzenia strażnika do granic jego pola widzenia - zarówno w lewo, jak i w prawo - kąt wynosi \(85^{\circ}\). Musimy tylko obliczyć \(\cos 85^{\circ} \dot= 0{,}087\). Zatem iloczyn punktów między kierunkiem patrzenia strażnika a znormalizowanymi wektorami kierunku do widocznych obiektów będą mieścić się w zakresie od około \(0{,}087\) do \(1\).
Na liście atrybutów powiązanych ze strażnikiem dodajemy nie tylko ich kierunek widzenia, ale także próg, który definiuje ich pole widzenia. Korzystając z tego progu, możemy sprawdzić, czy strażnik widzi danego gracza. Dla uproszczenia zaokrąglamy poprzedni wynik do jednego miejsca po przecinku i ograniczamy pole widzenia strażnika przy użyciu wartości progowej wynoszącej \(0{,}1\).
Zadanie 7. Określ, czy strażnik znajdujący się w punkcie początkowym widzi gracza \(A=[3;-2]\), biorąc pod uwagę, że kierunek patrzenia strażnika to \(\left(\frac{1}{\sqrt{5}};\frac{2}{\sqrt{5}}\right)\) a próg dla pola widzenia strażnika jest ustawiony na \(0{,}1\).
Rozwiązanie. Kierunek patrzenia strażnika jest już znormalizowanym wektorem. Musimy więc tylko znormalizować wektor kierunku od strażnika do gracza \(A\). Ponieważ strażnik znajduje się w punkcie początkowym, jest to równoważne normalizacji wektora \(\vec{a}=(3;-2)\). Otrzymujemy:
\[ \hat{a}=\frac{\left(3;-2\right)}{3^2+(-2)^2} = \frac{\left(3;-2\right)}{15} = \left(\frac{3}{15};\frac{-2}{15}\right). \]
Teraz obliczamy iloczyn kropkowy dwóch znormalizowanych wektorów:
\[ \left(\frac{1}{\sqrt{5}};\frac{2}{\sqrt{5}}\right) \cdot \left(\frac{3}{\sqrt{15}};\frac{-2}{\sqrt{15}}\right) = \frac{3}{\sqrt{75}} - \frac{4}{\sqrt{75}} = -\frac{1}{\sqrt{75}} \dot= -0{,}12. \]
Ponieważ wynik nie mieści się w przedziale od \(0,1\) do \(1\), strażnik nie widzi gracza \(A\). Co więcej, ujemny wynik wskazuje, że kąt między wektorami jest większy niż kąt prosty.
Zastanów się, jak zmieniłaby się sytuacja, gdyby strażnik nie znajdował się w punkcie początkowym.