Miura-Ori
 15 min.,
15 min.,  1/3
1/3 Miura-ori (składanie Miura) jest jednym z najbardziej znanych sposobów składania papieru w origami. Kiedy słyszymy słowo origami, prawdopodobnie najpierw wyobrażamy sobie papierowy model w kształcie zwierzęcia lub łodzi. Te proste kształty często stanowią pierwszy krok do fascynującego świata składania papieru. Istnieją jednak również dzieła origami, których wykonanie wymaga kilku godzin, a nawet dni umiejętnej pracy.
Fascynujące jest to, że zasada składania, jaką znamy z origami, występuje również w otaczającej nas przyrodzie i w nas samych. Stopniowo otwierający się pączek kwiatu, delikatnie rozkładające się skrzydła owadów ukryte pod pokrywami skrzydłowymi (utwardzonymi przednimi skrzydłami), złożona struktura ludzkiego DNA lub ściany jelita grubego – wszystkie one wykorzystują zasady podobne do tych stosowanych w origami. Zdolność materiałów i struktur do „składania się” i „rozkładania” w razie potrzeby jest jednym z podstawowych elementów budujących życie.
W ostatnich latach origami przeżywa prawdziwy boom, nie tylko jako hobby dla miłośników papieru, ale także w wielu dziedzinach sztuki i nauki. Wpłynęło ono na architektów, projektantów mebli, artystów i naukowców. Origami przekształciło się zatem z zwykłej sztuki składania papieru w narzędzie, które pomaga kształtować przyszłość.
Origami w nauce
Jednym z obszarów, w których origami znalazło zastosowanie, jest program kosmiczny. Podczas transportu dużych obiektów w kosmosie muszą one być składane do mniejszych rozmiarów. Jednym z takich obiektów jest osłona gwiezdna — gigantyczna tarcza zaprojektowana w celu blokowania światła gwiazdy. Astronomowie używają jej do obserwacji planet znajdujących się w pobliżu jasnych gwiazd, których blask uniemożliwiałby obserwację.
Wykorzystanie origami w robotyce również ma swoje zalety. Roboty zaprojektowane z wykorzystaniem origami mogą być szybsze, tańsze i łatwiejsze w produkcji niż roboty tworzone przy użyciu tradycyjnych technik.
Pojawiają się nowe rodzaje materiałów wykorzystujących struktury origami. Wzory tych struktur origami często opierają się na okresowym podziale płaszczyzny. W poniższych ćwiczeniach przyjrzymy się najbardziej znanemu wzorowi i metodzie składania papieru.
Zastosowanie Miura-Ori i technika składania
Ta technika składania została wynaleziona przez japońskiego astrofizyka Koryo Miurę. Po rozłożeniu struktura wygląda tak, jakby była podzielona na rzędy równoległoboków.
Ten konkretny wzór można rozłożyć lub złożyć w jeden prosty sposób. Wystarczy pociągnąć za jeden róg, aby rozłożyć origami przy minimalnym wysiłku. Miura zaprojektował tę metodę składania dla paneli słonecznych. W 1995 roku panel słoneczny wykorzystujący ten projekt został zainstalowany na japońskim satelicie Space Flyer Unit. Od tego czasu technika ta znalazła wiele innych zastosowań, w tym przenośne panele słoneczne i składane osłony kuloodporne dla policji. W Japonii mapy są również składane w ten sposób, aby uniknąć zużycia i zniszczenia rogów.
Wzór ten jest również stosowany w inżynierii materiałowej jako wewnętrzna część konstrukcji warstwowej. Wykonany z papieru kevlarowego, płyty pilśniowej lub folii plastikowej i umieszczony pomiędzy dwiema warstwami okładki, tworzy lekką konstrukcję, która jest bardzo wytrzymała i stabilna.
Spróbujmy złożyć ten wzór. Możemy zacząć od standardowego arkusza papieru formatu A4, który ma wymiary 210 mm x 297 mm. Aby wzór można było płynnie otwierać i zamykać, zaleca się podzielenie boków na nieparzystą liczbę sekcji. Zaczynamy od podzielenia krótszego boku arkusza A4 na 5 równych części, tak aby każda część miała długość 42 mm. Następnie łączymy przeciwległe punkty i składamy papier wzdłuż tych linii w harmonijkę.

Teraz podziel jedną z dłuższych krawędzi na 7 równych części. Przez każdy punkt podziału narysuj linię, która tworzy kąt nieprostopadły z dłuższą krawędzią. Przez pozostałe punkty podziału narysuj linie równoległe do tej linii.

Składamy harmonijkę wzdłuż tych równoległych linii. W tym momencie wszystkie zagięcia niezbędne do uzyskania ostatecznego wzoru są już na swoim miejscu — ale niektóre z nich są złożone w niewłaściwym kierunku.

Rozkładamy i układamy harmonijkę tak, aby poszczególne linie zagięcia tworzyły naprzemienne grzbiety i doliny.

Fałdy wzoru Miura-ori są oznaczone w origami tak jak na poniższym obrazku, tj. grzbiety są ciągłe, a doliny przerywane.
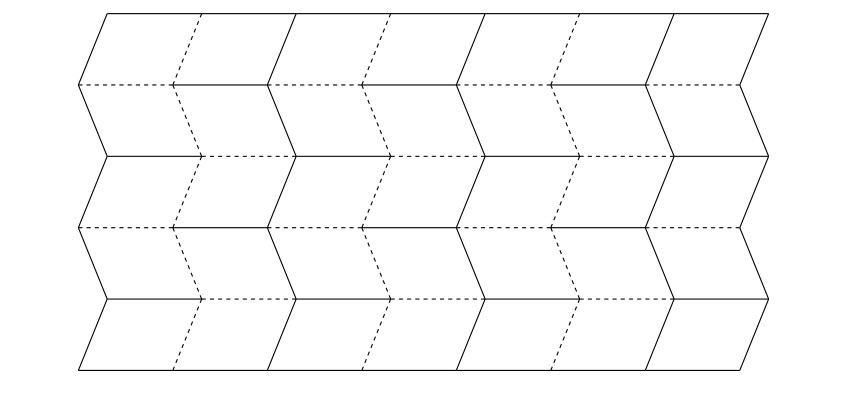
Ćwiczenie 1. Poniższy rysunek przedstawia dwie wersje końcowego wzoru po złożeniu (przy użyciu tego samego rozmiaru papieru i liczby podziałów). Jakie parametry mają wpływ na długość końcową?

Rozwiązanie. Z prostego porównania wzorów jasno wynika, że długość powstałego wzoru zależy od kąta, pod którym linie tworzą kąt nieprostopadły z dłuższym bokiem. Jest to oczywiste, ponieważ jest to jedyny czynnik, który powoduje różnice między wzorami. Oznaczmy ten kąt ostry przez \(\alpha\). Jeśli kąt \(\alpha\) będzie ostrzejszy, długość złożonego wzoru wzrośnie. Im bliżej \(90^\circ\) jest ten kąt, tym krótszy będzie złożony wzór.

Do tej pory porównaliśmy dwa różne wyniki oparte na podobnych podziałach. Ale w jaki sposób długość złożonego wzoru zależy od kąta \(\alpha\) i innych parametrów? Aby dokładniej zbadać tę zależność, warto skupić się na podstawowej części wzoru.
Ćwiczenie 2. Poniższy rysunek przedstawia podstawową część wzoru Miura-ori w postaci rozłożonej i złożonej. W jaki sposób zaznaczona długość \(x\) zależy od wielkości kąta \(\alpha\) oraz długości \(d\) i \(l\)?
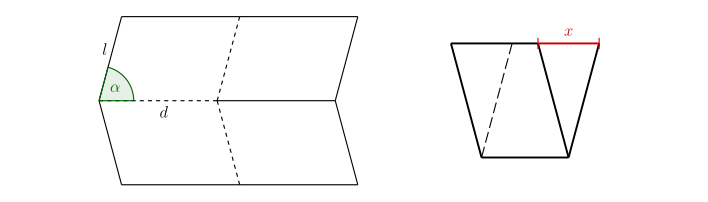
Rozwiązanie. Ważne jest, aby zaznaczyć parametry na obrazie w odpowiednich miejscach.
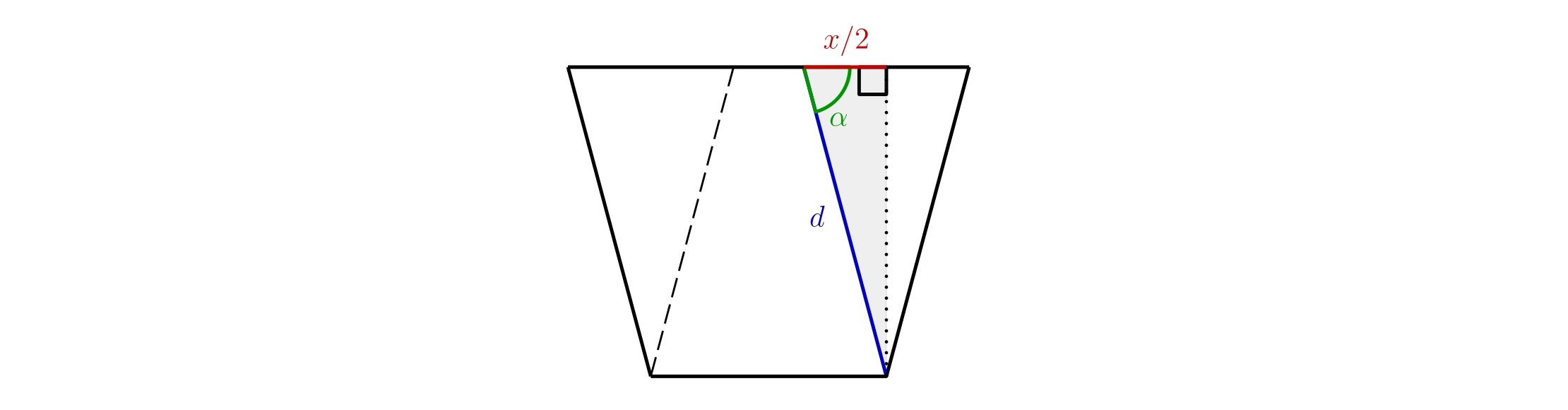
Dla \(\cos\alpha\) otrzymujemy zatem
\[ \cos\alpha = \frac{\frac{x}{2}}{d} = \frac{x}{2d},\]
z czego po prostu wyrażamy
\[ x = 2d \cdot \cos\alpha.\]
Długość \(x\) nie zależy zatem w ogóle od \(l\), ale tylko od kąta \(\alpha\) i długości \(d\).
Literatura i źródła
- https://www.youtube.com/watch?v=uFyJykl1O0k
- https://www.youtube.com/watch?v=ZVYz7g-qLjs
- https://laughingsquid.com/millidelta-small-origami-inspired-robot/
- https://www.jpl.nasa.gov/news/solar-power-origami-style
- https://en.wikipedia.org/wiki/File:NASA_Starshade_animation.webm