Rozmanitost ekosystémů na ostrovech
 30 min.,
30 min.,  2/3
2/3 V tomto textu si ukážeme, proč jsou logaritmy důležité v biologických vědách a ve vědách o živé přírodě.
Život v přírodě je neustálým bojem o přežití, kdy se živočichové nebo rostliny musí postarat o přežití svého druhu. Pro zvířata toto například zahrnuje schopnosti a síly uniknout predátorům, zajistit si potravu a hnízdiště, rozmnožit se a ochránit potomky, než tito budou schopni samostatného života. K dosažení tohoto cíle je nutný mimo jiné dostatek životního prostoru. Tedy žít na území s dostatkem zdrojů (potravy, hnízdišť a podobně). A množství zdrojů přímo souvisí s velikostí území.
Biologové znají zákon udávající vztah mezi počtem druhů žijících trvale v ekosystému a plošnou rozlohou tohoto ekosystému. Zákon (angl. species-area relationship) má tvar
\[N=c A^k,\tag{1}\]
kde \(N\) je počet druhů, \(A\) je plošná rozloha území a \(c\) a \(k\) jsou konstanty. Konstanta \(c\) závisí na jednotkách obsahu a udává, jaký je teoretický počet druhů na oblasti o jednotkové rozloze. Konstanta \(k\) má typicky hodnoty mezi \(0{,}2\) a \(0{,}35\) pro ostrovy a \(0{,}12\) až \(0{,}17\) pro pevninu.
Vztah (1) byl experimentálně potvrzen například na mangrovových ostrůvcích u Floridy. To jsou malé ostrůvky, v podstatě stromy, vyrůstající z brakické vody mělkého moře. Vzhledem k malým rozměrům ostrova bylo možno zkoumat, jak ekosystém reaguje na změnu rozlohy ostrova. Výzkumníci motorovou pilou zmenšili rozlohu a sledovali odpovídající snížení počtu druhů. Kromě toho byly prováděny pokusy s kolonizací neobydleného ostrova. V takovém případě se na ostrůvku chemicky zničil život podobně, jako se provádí desinfekce domů. Poté vědci pozorovali, že druhové bohatství se samovolně obnovilo na původní stav. Zajímavostí je, že počet druhů zůstal stejný, ale konkrétní druhy se obměnily. Některé druhy byly nahrazeny druhy jinými.
Protože vztah (1) je mocninná funkce s obecným neceločíselným exponentem, není závislost mezi rozlohou ekosystému a počtem druhů jednoduše indetifikovatelná z naměřených nebo vypozorovaných dat. Přesto je důležité tuto funkční závislost znát. Pomáhá nám to například v ochraně přírody. Ekosystémem v uvedeném kontextu je sice zpravidla ostrov, ale bývá tím míněn jakýsi zobecněný ostrov: nejenom pevnina obklopená mořem, ale jakékoliv území umístěné do území jiného typu. Například tedy může jít o jezero uvnitř souše, o lesík v zemědělské krajině, nebo o chráněnou krajinnou oblast obklopenou přírodou s běžným režimem. Znalost toho, jak souvisí velikost území s druhovou skladbou a druhovou pestrostí je důležitým faktorem pro rozhodování, jestli při ochraně přírody budovat jednu velkou rezervaci nebo několik malých.
S podobným zákonem jako je vztah (1) se v biologii setkáváme velice často v alometrických vztazích. To jsou vztahy, kde se fyzické a fyziologické vlastnosti organismů mění v závislosti na velikosti organismu. Například závislost doby potřebné k dosažení dospělosti na tělesné hmotnosti má podobný průběh, viz Begon (1997). Jiným příkladem je Kleiberův zákon udávající vztah mezi hmotností živočicha a jeho bazálním metabolismem.
V následujících úkolech vyřešíme úlohy související se vzorcem (1) a ukážeme si, jak k práci s ním můžeme využít logaritmy.
Úlohy
Úloha 1: Ukažte, že po zlogaritmování vztahu (1) je výsledná závislost lineární, tj. pokud na osy vynášíme namísto velikosti území a počtu druhů jejich logaritmy, tak grafem závislosti bude přímka.
Řešení. Vyjdeme ze vztahu (1), tj. \[N=c A^k.\]
Logaritmováním dostáváme
\[\log N= \log (c A^k).\]
Odsud po použití pravidla pro logaritmus součinu a logaritmus mocniny dostáváme
\[\log N= \log (c) + k\log A.\]
Nyní substituce \(y=\log N\), \(q = \log c\), \(x=\log A\) převádí rovnici na
\[y=kx+q,\]
což je rovnice přímky se směrnicí \(k\).
Poznámka: Protože není pohodlné při vynášení každé hodnoty do grafu počítat dva logaritmy, používají se takzvané logaritmické osy. Vzdálenost bodu \(x\) od bodu 1 je \(\log x\) a toto měřítko je použito pro vodorovnou i svislou osu.
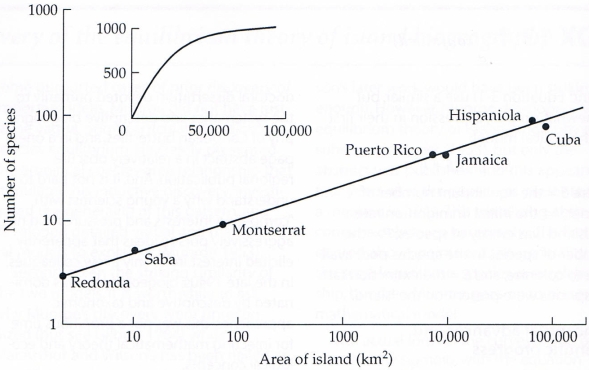
Připojený obrázek ukazuje, jak se při použití logaritmických os mocninná závislost mění na lineární. Graf zachycuje počty druhů plazů a obojživelníků na ostrovech v Západní Indii (angl. West Indies, antilské ostrovy a bahamské souostroví). Díky použití logaritmických os jsou data téměř přesně vyrovnána v jedné přímce. Tato vlastnost je snadno detekovatelná jak opticky z dat, tak i pomocí matematických postupů. Vložený menší obrázek ukazuje, jak by závislost vypadala bez použití logaritmických os. Data leží v oblouku křivky, o níž na první pohled není patrné, jestli se jedná o mocninnou křivku, nebo exponenciální, či nějakou jinou závislost.
Úloha 2: Je odhadnuto, že pro jisté území je hodnota exponentu \(k\) rovna \(0{,}15\). Jak se sníží počet druhů, pokud se plocha sníží na desetinu? Tato úloha modeluje například rozsáhlé kácení lesa.
Řešení. Vyjdeme ze zákona \[N(A)=c A^k\] a hodnotu plochy snížíme na desetinu. \[N(0{,}1A) = c\cdot(0{,}1 A)^k = c A^k \cdot 0{,}1^k = N(A)\cdot 0{,}1^k\] Odsud pro \(k=0{,}15\) dostáváme \[\frac{N(0{,}1A)}{N(A)}=0{,}1^k = 0{,}71.\] Po snížení rozlohy na desetinu klesne počet živočišných druhů na 71 procent původního stavu, tj. klesne o 29 procent.
Úloha 3: Bylo vypozorováno, že po snížení rozlohy na čtvrtinu klesne počet druhů na sedmdesát procent původního stavu. Odhadněte velikost parametru \(k\).
Řešení. Původní hodnoty pro velikost rozlohy a počet druhů označíme \(A_1\) a \(N_1\). Nové hodnoty budou \(A_2\) a \(N_2\). Obě sady dat vyhovují rovnici (1) a proto \[N_1 = c A_1^k\] a \[N_2 = c A_2^k.\] Vydělením těchto vztahů dostáváme \[\frac{N_1}{N_2} = \frac{c A_1^k}{ c A_2 ^k} =\left(\frac {A_1}{A_2}\right)^k.\] Podle zadání platí \(N_2=0{,}7N_1\) a \(A_2=0{,}25A_1\), tj. \[\frac{N_1}{0{,}7N_1}=\left(\frac{A_1}{0{,}25A_1}\right)^k\] \[\frac{1}{0{,}7}=\left(\frac{1}{0{,}25}\right)^k.\] Logaritmováním obdržíme \[\log\frac{1}{0{,}7}=k\cdot\log\frac{1}{0{,}25}.\] a odtud \[k=\frac{\log \frac1{0{,}7}}{\log 4}\approx 0{,}257.\]
Literatura
- Teorie ostrovní biogeografie, ENVI WIKI, https://www.enviwiki.cz/w/index.php?title=Teorie_ostrovn%C3%AD_biogeografie, October 3, 2023
- Co je ostrovní biogeografie?, https://zemepisec.cz/biogeografie/ostrovni/, October 3, 2023
- Species–area relationship, Wikipedie, https://en.wikipedia.org/wiki/Species%E2%80%93area_relationship, October 3, 2023
- Culek M., Biogeografie, https://is.muni.cz/el/1431/jaro2010/Z0005/18118868/index_book_3-1-1.html, October 3, 2023
- Begon, M. et al. Ekologie: jedinci, populace a společenstva : [Investice do rozvoje vzdělávání, reg.č.: CZ1.07/2.2.00/15.0084]. 1st ed. Olomouc: Vydavatelství Univerzity Palackého, 1997. 949 p. ISBN 80-7067-695-7.