Podíváme se na možné praktické využití goniometrických funkcí a vztahů mezi délkami stran pravoúhlého trojúhelníka.
Budeme se zabývat problematikou lepených spojů. Ukážeme si metody, jak rozložit silové namáhání spoje na více složek a na větší plochu a jak určit napětí, které vzniká při namáhání takového spoje. Vypočteme, jak se změní napětí ve spoji při osovém namáhání tyče nebo nosníku, který není slepen čely, ale spoj je veden šikmo, jak je vidět na obrázku.
Ze života každý zná spojování materiálů lepením. Pokud na pevnosti výsledného spoje nezáleží, je lepení jedním z nejjednodušších způsobů spojování materiálů. V praxi ovšem často potřebujeme, aby spoj byl trvanlivý a pevný. Tedy aby unesl velké silové zatížení.
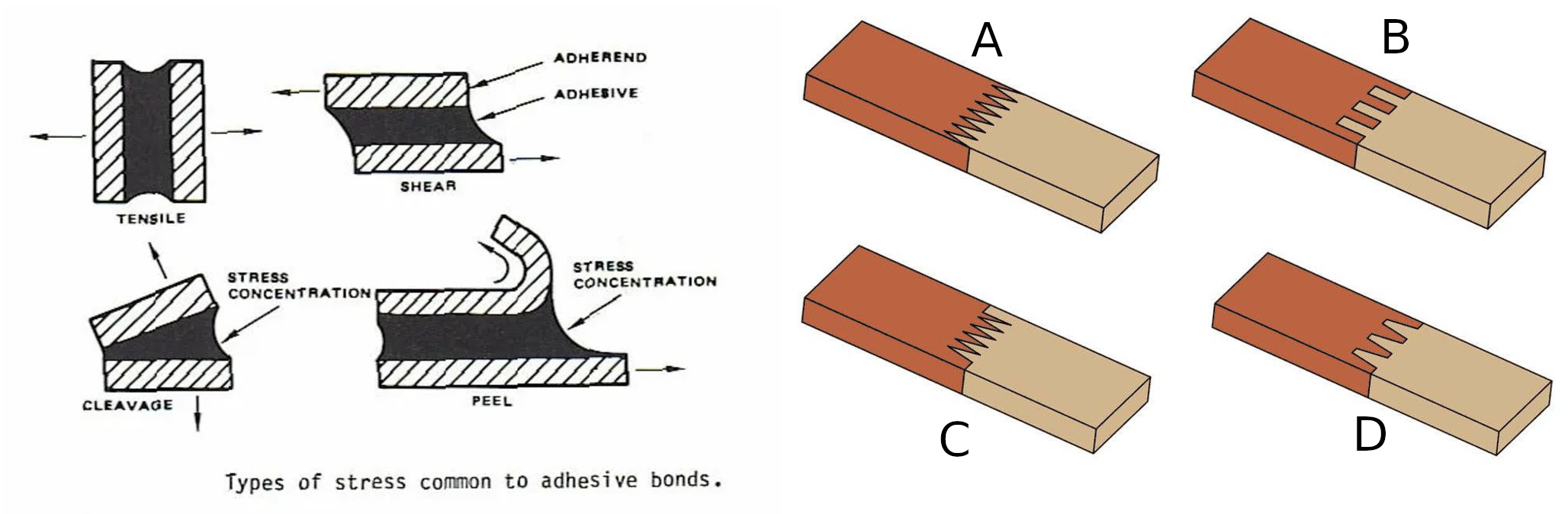
Lepidla garantují zpravidla odolnost vůči normálovému namáhání tahem a vůči namáhání smykem, které nepřekročí hodnoty dané výrobcem lepidla. Mechanické napětí vznikající při namáhání spoje silnou je podílem působící síly a plochy, na kterou síla působí. V případě normálového napětí je uvažována síla kolmá na plochu, v případě namáhání smykem je síla rovnoběžná s plochou. Možné deformace namáhaného spoje
jsou na obrázku vlevo, přičemž “Tensile” ilustruje normálové namáhání tahem a “Shear” smykové namáhání.
Odolnost spoje souvisí s použitým lepidlem a s lepenými materiály. Údaje lze nalézt u výrobců a mohou vypadat například takto:
Protože napětí ve spoji se určuje jako podíl síly a plochy, pro jeho snížení se snažíme rozložit silové působení do více směrů a na větší plochu. Ukázkou jsou spoje na předchozím obrázku vpravo. U spoje B jsou čelní plochy namáhané normálovým napětím doplněny plochami namáhanými čistě smykovým napětím.
Pro nás bude zajímavější spojení šikmým spojem, protože při něm je spoj vystaven současně normálovému i smykovému namáhání. Poznamenejme, že v praxi šikmý spoj často vidíme realizovaný jinak, než je na úvodním obrázku. Důvod je ten, že je výhodnější mít spoj více skloněný, ale příliš šikmý spoj by zabíral velký prostor. V praxi je proto takový spoj realizován s přerušeními, s otočením každé druhé části a se zarovnáním jednotlivých částí nad sebe.
Úloha 1. Uvažujme hranol o šířce \(b=4\,\mathrm{cm}\) a výšce \(h=3\,\mathrm{cm}\), který je slepen ze dvou kusů šikmým spojem podle obrázku. Spoj svírá s čelem hranolu úhel o velikosti \(\alpha=30^\circ\). Hranol je namáhán v ose silou \(F=1\,000\,\mathrm{N}\). Vypočtěte namáhání spoje a porovnejte s namáháním v řezu kolmém na osu.
Řešení. V rovině kolmé na osu má řez tvar obdélníka se stranami \(b\) a \(h\). Síla \(F\) vyvolá v této rovině tahové napětí \[ \sigma = \frac{F}{bh} = \frac{1000\,\mathrm{N}}{3\times 4 \,\mathrm {cm}^2} = 833\,333\ \mathrm{Pa} = 0{,}833\, \mathrm{MPa}. \]
Normálové napětí \(\sigma_N\) ve spoji vypočteme vztahem \[\sigma_N = \frac{F_N}{S},\] kde \(F_N\) je velikost normálové síly a \(S\) je obsah plochy spoje. Smykové napětí \(\sigma_G\) vypočteme podobně jako normálové vztahem \[\sigma_G = \frac{F_G}{S},\] kde \(F_G\) je velikost smykové síly.
V pravoúhlém trojúhelníku s přeponou \(F\) a odvěsnami \(F_N\) a \(F_G\) (viz. Obrázek 5) můžeme určit vnitřní úhly díky vlastnostem doplňkového a souhlasných úhlů. Z tohoto trojúhelníka, pak získáme velikosti sil \(F_N\) a \(F_G\):
\[ \begin{aligned} F_N&=F\cos \alpha\\ F_G&=F\sin \alpha \end{aligned} \]
Spoj bude mít tvar obdélníka. Jedna jeho strana bude rovna šířce hranolu \(b\). Délku \(c\) druhé strany určíme jako délku přepony pravoúhlého trojúhelníka, ve kterém známe délku odvěsny \(h\) a velikost úhlu \(\alpha\) mezi odvěsnou a touto stranou.
Tedy \[ c=\frac{h}{\cos \alpha} \] a \[S=bc=\frac{hb}{\cos\alpha}.\]
S využitím odvozených vztahů dostáváme pro normálové napětí hodnotu \[ \sigma_N = \frac{F_N}{S} = \frac {F\cos\alpha}{\frac{hb}{\cos \alpha}} = \frac{F}{hb}\cos^2\alpha = \sigma \cos^2\alpha \] a pro smykové napětí hodnotu \[ \sigma_G = \frac{F_G}{S} = \frac {F\sin\alpha}{\frac{hb}{\cos \alpha}} = \frac{F}{hb}\sin\alpha\cos\alpha = \sigma \sin\alpha\cos\alpha. \]
Hodnoty faktorů \(\cos^2\alpha\) a \(\sin\alpha \cos \alpha\) udávají, kolikrát se změní normálové nebo smykové napětí ve spoji v porovnání s napětím v kolmém řezu. Protože jsou pro nenulový úhel oba faktory menší než jedna, budou obě hodnoty \(\sigma_N\) i \(\sigma_G\) menší než \(\sigma\). Průběh funkcí \(\sin x\cos x\) a \(\cos^2x\) pro \(x\) ve stupních je na obrázku níže. Pro úhel \(\alpha=30^\circ\) a zadané parametry hranolu a silového působení dostáváme \[ \sigma_N=0{,}625\,\mathrm{MPa} \] a \[ \sigma_G=0{,}361\,\mathrm{MPa}. \]
Úloha 2. Určete, pro jaký úhel bude smykové napětí ve spoji podle Úlohy 1 maximální. Určete i odpovídající normálové napětí.
Řešení.
V Úloze 1 byl odvozen vzorec pro smykové napětí ve tvaru
\[ \sigma_G=\sigma\sin\alpha\cos\alpha. \]
Užitím vzorce pro dvojnásobný úhel dostáváme
\[ \sigma_G=\frac 12\sigma\sin(2\alpha). \]
Funkce \(\sin 2\alpha\) má maximum pro úhel \(\alpha = 45^\circ\), viz i Obrázek 6 v řešení Úlohy 1. Odsud vidíme, že maximální hodnota smykového napětí je pro úhel \(\alpha=45^\circ\) a v tomto případě bude platit \(\sigma_G=\frac 12\sigma\).
Pro normálové napětí jsme odvodili vzorec
\[\sigma_N=\sigma \cos^2\alpha\]
a pro \(\alpha=45^\circ\) dostáváme \(\sigma_N=\frac 12\sigma.\) Při maximálním smykovém napětí tedy budou obě napětí (smykové i normálové) stejné a rovny polovině hodnoty \(\sigma\). Tato situace nastane pro spoj pod úhlem \(45^\circ\).
Úloha 3. Lepidlo garantuje že spoj odolá namáhání, při kterém vzniká normálové napětí \(10\,\mathrm{MPa}\) a smykovém napětí \(8\,\mathrm{MPa}\). Jaká maximální síla může zatížit spoj z Úlohy 1? Jak by se odpověď na tuto otázku změnila pro spoj pod úhlem \(45^\circ\)?
Řešení. V Úloze 1 byly odvozeny vztahy mezi oběma napětími a působící silou \[ \sigma _N=\frac{F}{bh}\cos^2 \alpha \] a \[ \sigma _G=\frac{F}{bh}\sin \alpha \cos \alpha. \] Odsud vyjádříme sílu jako funkci jednotlivých napětí. Protože se bude jednat o kritickou hodnotu síly, při které spoj selhává, označíme ji \(F_{\max,N}\) pro sílu, kdy je kritické hodnoty dosaženo pro normálové napětí a \(F_{\max,G}\) pro sílu, kdy je dosaženo kritické hodnoty pro smykové napětí. Dostáváme \[ F_{\max, N}=\frac{bh\sigma_N}{\cos^2\alpha} \]
a
\[ F_{\max, G}=\frac{bh\sigma_G}{\sin\alpha\cos\alpha}. \]
Pro rozměry z Úlohy 1 a pro zadané \(\sigma_N=10\,\mathrm{MPa}\) a \(\sigma_G=8\,\mathrm{MPa}\) vypočteme
\[ F_{\max, N}=\frac{3\times 4 \,\mathrm{cm}^2 \times 10\,\mathrm{MPa}}{\cos^2 30^\circ}=16\,000\,\mathrm{N} \]
a
\[ F_{\max, G}=\frac{3\times 4 \,\mathrm{cm}^2 \times 8\,\mathrm{MPa}}{\sin 30^\circ\cos 30^\circ}=22\,170\,\mathrm{N}. \]
Ani jedna z těchto hodnot nesmí být překročena. Maximální síla, která může zatížit tento spoj, je tedy \(16\,000\,\mathrm{N}\).
Pro úhel \(\alpha = 45^\circ\) dostáváme podobně hodnoty
\[F_{\max, N}=\frac{3\times 4 \,\mathrm{cm}^2 \times 10\,\mathrm{MPa}}{\cos^2 45^\circ}=24\,000\,\mathrm{N}\]
a
\[F_{\max, G}=\frac{3\times 4 \,\mathrm{cm}^2 \times 8\,\mathrm{MPa}}{\sin 45^\circ\cos 45^\circ}=19\,200\,\mathrm{N}.\]
I v tomto případě nesmí být překročena ani jedna z uvedených hodnot. Odsud vidíme, že spoj pod úhlem \(45^\circ\) může být zatížen silou maximálně \(19\,200\,\mathrm{N}.\)
Studovali jsme síly, které se snaží porušit spoj normálovým namáháním kolmo na spoj a smykovým namáháním. Kromě toho silové působení může ještě v rovině spoje natahovat spoj jako celek. V uvedené analýze nás tato komponenta nezajímala. Je však možné ji obdržet ze vzorce pro normálové napětí \(\sigma_N\) otočením o úhel 90 stupňů.
Rozklad namáhání do předem zvolených směrů se používá i v jiných situacích inženýrské praxe, než je lepení. Například pokud je uvnitř namáhaného materiálu trhlina, znalost silového působení umožní zhodnotit rizika dalšího šíření tohoto defektu. Je potom přirozené mechanické namáhání transformovat do směru defektu podobně, jako jsme transformovali do směru spoje.
Mechanické namáhání je vhodné transformovat do zkoumaných směrů i při studiu deformace kompozitních materiálů. Může se jednat o umělé kompozity nebo i o kompozity přírodní. Umělé kompozity jsou například materiály vyztužené vlákny. Mezi přírodní kompozity patří i nejrozšířenější konstrukční materiál, dřevo. Tyto kompozity mají díky své struktuře v různých směrech různé vlastnosti a při studiu mechanického působení na takové materiály je jednodušší studovat odděleně namáhání ve směrech, které souvisejí se strukturou tohoto kompozitu. Například namáhání ve směru ztužujících vláken u umělých kompozitů nebo namáhání v podélném směru (po letech) u dřeva. Obecně se jedná o namáhání v osách nebo rovinách symetrie materiálu. V těchto směrech je známa reakce materiálu na namáhání. Reakci na namáhání v jiných směrech můžeme určit tak, že namáhání rozložíme do jednotlivých směrů, určíme odpovídající deformace a informace opět složíme abychom získali celkovou reakci materiálu. Inženýři tuto problematiku znají jako tzv. transformaci tenzorů a mají celou řadu technik, jak rychle a efektivně úlohy zadaného typu řešit.