Zdravotní stav stromu je důležité znát například v městských parcích kvůli bezpečnosti obyvatel. Kontrolují se hlavně staré stromy, u nichž je pravděpodobnější, že by nemusely být zdravé. Kmen poškozeného či nemocného stromu se může při zvýšené intenzitě větru zlomit a způsobit někomu zranění nebo hmotné škody. Podobně i majitelé menších nemovitostí často mají v blízkosti domu starý strom a nechtějí riskovat, že by při pádu poškodil například střechu.
Zdraví stromu je schopen posoudit arborista, který kontroluje, zda strom prospívá nebo začíná schnout. Po obvodu stromu hledá dřevokazné houby a také místa, která jsou viditelně poškozená. Své pozorování může doplnit měřením stromovým tomografem nebo tahovou zkouškou. Poté může navrhnout různá opatření zvyšující bezpečnost. Například prořezání větví v koruně stromu, aby v případě velkého větru příliš nezatěžovala kmen apod.
Často používanými metodami neinvazivního posuzování zdravotního stavu stromů jsou tahová zkouška a akustická tomografie pomocí stromového tomografu.
Tato zkouška spočívá v tom, že se měří reakce stromu na jeho vychýlení kmene. V praxi se do určité výšky kmene přiváže lano a za ně se tahá. K patě kmene jsou umístěna čidla, která měří výslednou odezvu. Arborista má k dispozici mnoho vzorů, jak se má která dřevina chovat, a podle výsledků měření se porovnává konkrétní případ s nejlépe odpovídajícím vzorem. Výsledkem je zjištění, v jakém stavu je kořenový systém stromu, a zda se strom může zlomit v kmeni. Tato metoda je poměrně drahá. Měření trvá relativně dlouho a navíc je potřeba stromolezec, který vyleze na strom a přiváže k němu lano, a po ukončení měření ho zase sundá. V poslední době se proto už tato metoda moc nepoužívá, místo toho je lepší využít stromový tomograf.
Stromový tomograf funguje na principu přenosu zvuku. Po obvodu kmene stromu se v určité výšce umístí senzory na hřebech. Hřeby se zatlučou skrz kůru stromu až ke dřevu. Umísťují se vždy do aktivního rostlinného pletiva. Zde totiž strom dokáže velmi rychle regenerovat, a tak ho tyto hřeby nijak nepoškodí.
Arborista pak postupně klepe kladívkem na jednotlivé senzory. Přitom se měří rychlost, za kterou zvukový signál dorazí k ostatním senzorům. Zvuk prochází zdravým dřevem rychle, zatímco v případě vnitřních vad se jeho přenos zpomaluje. Porovnáním naměřené a referenční hodnoty se proto dá najít třeba dutina ve dřevě už v rané fázi jejího vývoje.
Z naměřených rychlostí přenosu zvuku se dá sestavit tzv. rychlostní graf (viz. Obrázek 3). U úseček, které spojují jednotlivé body je důležitá jejich barva. Ta udává rychlost, jakou zvukový signál prošel od jednoho bodu ke druhému. Počítačový program potom z naměřených rychlostí sestaví výsledný tzv. tomogram. Jde o dvourozměrný obraz, který znázorňuje zóny s různými vlastnostmi přenosu zvuku.
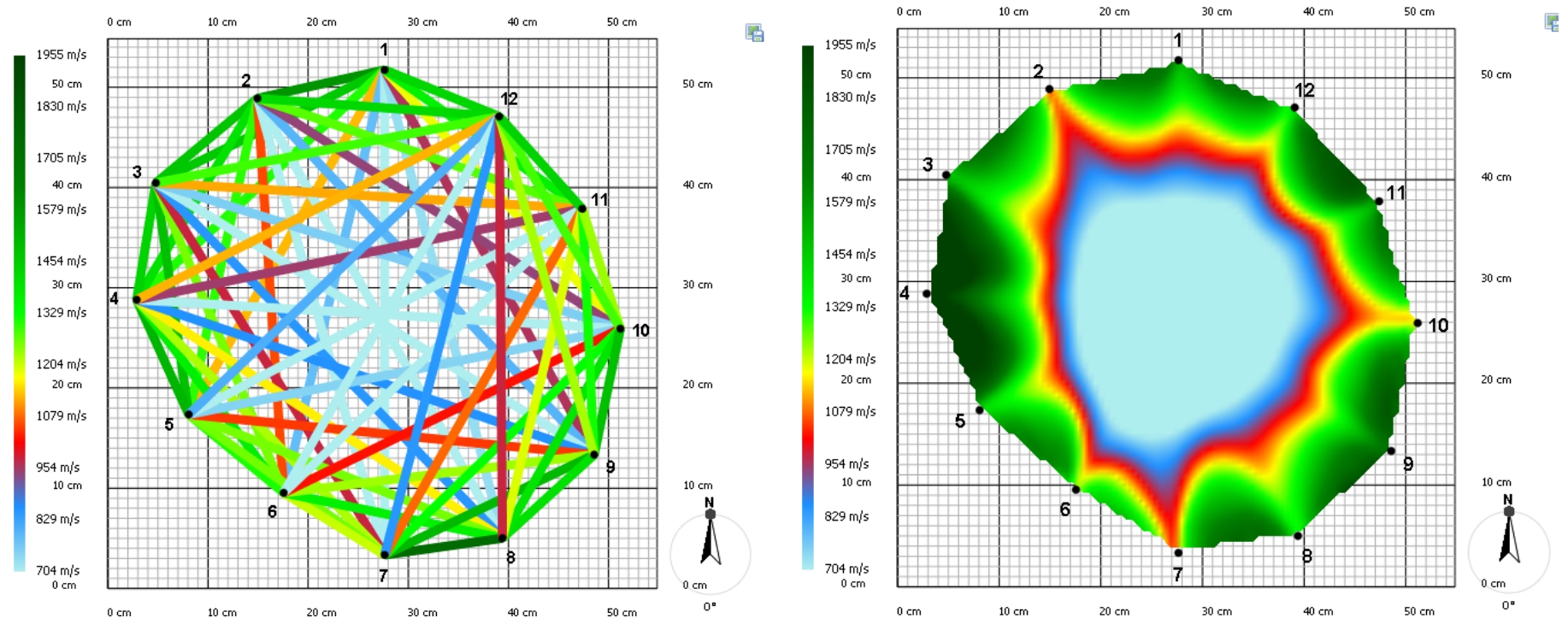
K posouzení stavu stromu arborista neproměřuje pouze jeden průřez, ale několik, přičemž se zaměřuje na viditelně poškozená místa na kmeni. Ze všech získaných informací si poté utvoří přehled o celkovém zdraví stromu.
Když je v kmeni zjištěna nějaká dutina, nemusí to ještě znamenat významný problém, pokud je vnější obvod kmene zdravý. Není možné přesně říct, kolik zdravého dřeva musí po obvodu být. To záleží na druhu dřeva, stáří stromu a na jeho průměru. Princip je stejný jako u ocelové trubky. Ta je taky pevná, i když je tyč dutá a materiál je jen po obvodu. Existuje zde několik pravidel. Jedno z nich říká, že je v pořádku, když je zdravá třetina průřezu kmene stromu. Jiné pravidlo tvrdí, že u velmi starých stromů postačí, když je po obvodu jen třícentimetrová vrstva zdravého dřeva.
Stromovým tomografem se dá poměrně přesně určit stav kořenového systému. Provede se měření úplně u země a pak v několika dalších výškách. Pokud z výsledků programu je vidět, že se hniloba šíří kmenem zespodu nahoru, je pravděpodobné, že kořeny také nejsou v pořádku.
I tomograf má své omezení. Měření se neprovádí v zimě když mrzne, protože zmrzlou mízou se zvuk šíří jinak a výsledek by mohl být zkreslený.
K sestavení tomogramu je potřeba znát vzdálenosti mezi všemi použitými senzory. Tato vzdálenost se dá změřit pomocí posuvného měřítka. U velmi starých a mohutných stromů však může být s posuvným měřítkem problém - jednoduše nemá potřebný rozsah. Co dělat, když se tedy nedají změřit všechny potřebné vzdálenosti mezi senzory? Pro jednoduchost problém omezíme na vzdálenosti mezi 4 senzory.
Úloha 1. Uvažujme obecný čtyřúhelník \(ABCD\). V tomto čtyřúhelníku známe délky všech 4 stran \(a\), \(b\), \(c\), \(d\) a délku \(u\) jedné úhlopříčky \(AC\). Délka \(v\) úhlopříčky \(BD\) už je příliš velká a nejde změřit naším měřidlem. Jak bychom mohli tuto délku zkonstruovat?
Řešení. Planimetrické řešení je samozřejmě nejjednodušší. Sestrojíme nejprve úsečku \(AC\). Jelikož známe délky stran čtyřúhelníka \(AB\) a \(BC\) můžeme nad úhlopříčkou \(AC\) sestrojit trojúhelník \(ABC\). Podobně sestrojíme trojúhelník \(ADC\) a pak už stačí jen změřit délku úhlopříčky \(BD\). V praxi postupujeme samozřejmě ve vhodném měřítku.
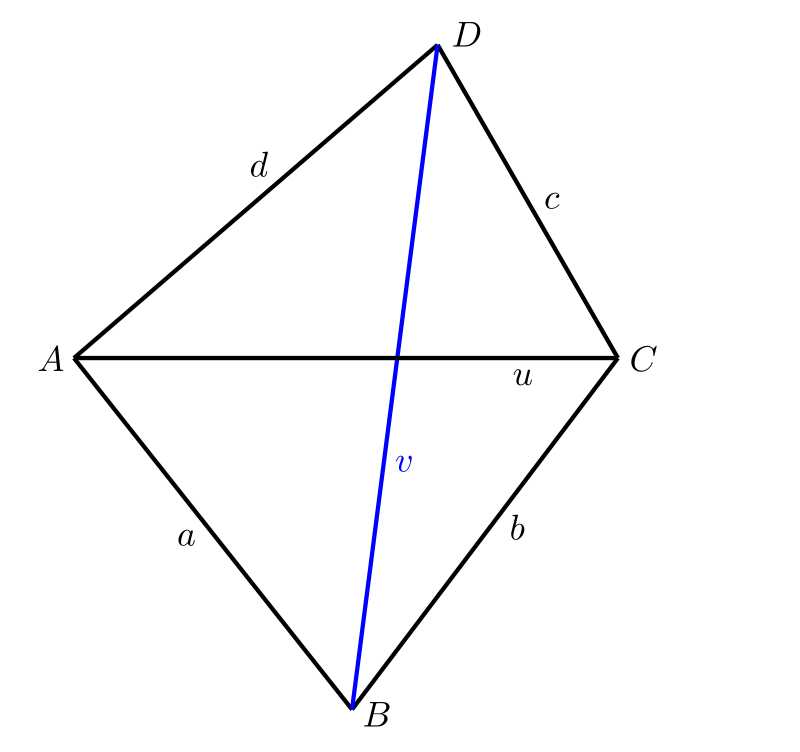
Řešení provedené tužkou na papír nebude příliš přesné. Narýsujeme-li však totéž v rýsovacím programu na počítači (můžeme použít třeba GeoGebru), přesnost výsledku už bude dostačující.
Problém je, pokud arborista tento výpočet musí provést ne jednou, ale mnohokrát. Pak už by planimetrické řešení bylo časově náročné a nevýhodné. Lepší by bylo mít program, stačila by tabulka v Excelu, kam by se zadaly naměřené hodnoty a chybějící délku by spočítal počítač.
Úloha 2. Problém z Úlohy 1 vyřešete analyticky.
Řešení. Začneme vhodnou volbou souřadné soustavy. Počátek souřadné soustavy umístíme do bodu \(A\), osu \(x\) zvolíme tak, aby na ní ležel bod \(C\). Pro naši volbu potom budou souřadnice vrcholů čtyřúhelníka \[A[0, 0],\; C[u, 0],\; B[b_1, b_2],\; D[d_1, d_2].\]
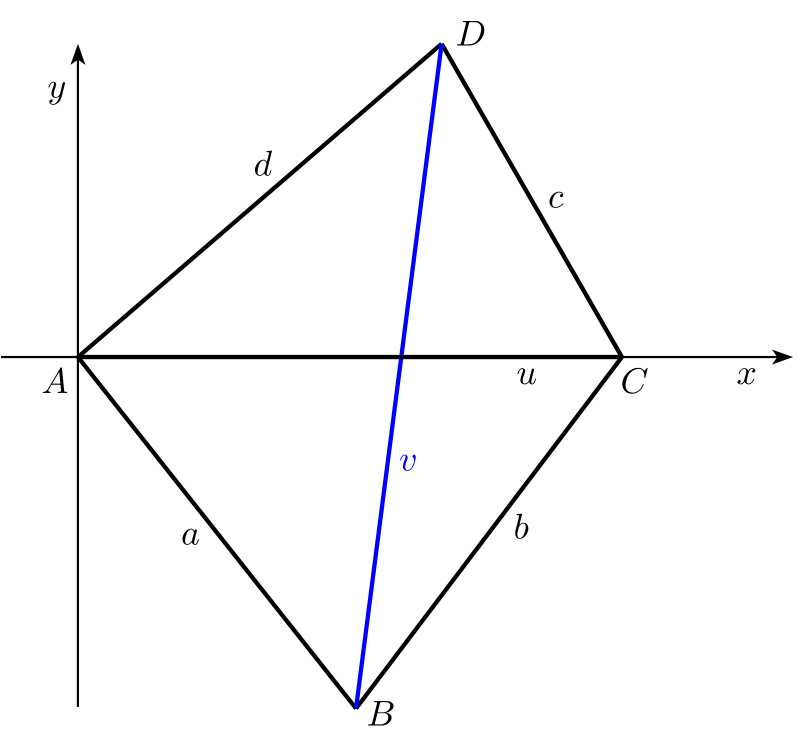
Potřebujeme určit souřadnice \(b_1\), \(b_2\), \(d_1\) a \(d_2\), pak už bude snadné vypočítat hledanou délku úhlopříčky \(v\) jako délku vektoru \(\overrightarrow{BD}\).
Nejprve budeme pracovat s trojúhelníkem \(\bigtriangleup ACD\), abychom získali souřadnice bodu \(D\). Určíme vektory \(\overrightarrow{AD}\) a \(\overrightarrow{CD}\)
\[ \begin{aligned} & \overrightarrow{AD} = D-A = (d_1,d_2),\\ & \overrightarrow{CD} = D-C = (d_1-u,d_2) \end{aligned} \] a vypočteme jejich délky \[ \begin{aligned} & \|\overrightarrow{AD}\| = \sqrt{d_1^2+d_2^2} = d,\\ & \|\overrightarrow{CD}\| = \sqrt{(d_1-u)^2+d_2^2} = c. \end{aligned} \] Umocněním dostáváme soustavu dvou rovnic o dvou neznámých \(d_1\) a \(d_2\) \[ \begin{aligned} & d_1^2+d_2^2 = d^2,\\ & (d_1-u)^2+d_2^2 = c^2. \end{aligned} \] Soustavu můžeme řešit například sčítací metodou. Po vynásobení druhé rovnice číslem \(-1\) a sečtením obou rovnic dostaneme \[2d_1u-u^2=d^2-c^2.\] Z této rovnice vyjádříme \[d_1=\frac{1}{2u}(d^2-c^2+u^2).\] Dosazením \(d_1\) do první rovnice získáme \[d_2^2=d^2-d_1^2,\] a odmocněním vypočteme \[d_2=\sqrt{d^2-d_1^2}.\]
Podobným způsobem z trojúhelníka \(\bigtriangleup ABC\) vypočíteme souřadnice bodu \(B\). Využijeme vektory \(\overrightarrow{AB}\) a \(\overrightarrow{CB}\). Vektory \[ \begin{aligned} & \overrightarrow{AB} = B-A = (b_1,b_2),\\ & \overrightarrow{CB} = B-C = (b_1-u,b_2) \end{aligned} \] mají délky \[ \begin{aligned} & \|\overrightarrow{AB}\| = \sqrt{b_1^2+b_2^2} = a,\\ & \|\overrightarrow{CB}\| = \sqrt{(b_1-u)^2+b_2^2} = b. \end{aligned} \] Umocněním získáme soustavu dvou rovnic pro dvě neznámé \(b_1\) a \(b_2\) \[ \begin{aligned} & b_1^2+b_2^2 = a^2,\\ & (b_1-u)^2+b_2^2 = b^2. \end{aligned} \] Odsud vypočteme \[b_1=\frac{1}{2u}(a^2-b^2+u^2).\] Z první rovnice pak máme \[b_2^2=a^2-b_1^2\] a odmocněním dostaneme \[b_2=-\sqrt{a^2-b_1^2}.\] Záporné znaménko v poslední rovnici je způsobeno tím, že bod \(B\) má \(y\)-ovou souřadnici zápornou (body \(B\) a \(D\) leží v opačných polorovinách určených přímkou \(AC\)).
Nyní už můžeme vypočítat hledanou délku úhlopříčky \(v\) jako délku vektoru \(\overrightarrow{BD}\) pomocí vztahu \[v=\|\overrightarrow{BD}\| = D-B = \sqrt{(d_1-b_1)^2+(d_2-b_2)^2}.\]
Úloha 3. Jak se situace zkomplikuje, přidáme-li další senzor \(Z\)? Opět známe vzdálenosti \(m\), \(n\) senzoru \(Z\) od senzorů \(A\) a \(D\) a chceme určit vzdálenost bodu \(Z\) od bodu \(B\), tedy délku další nezměřitelné úhlopříčky.
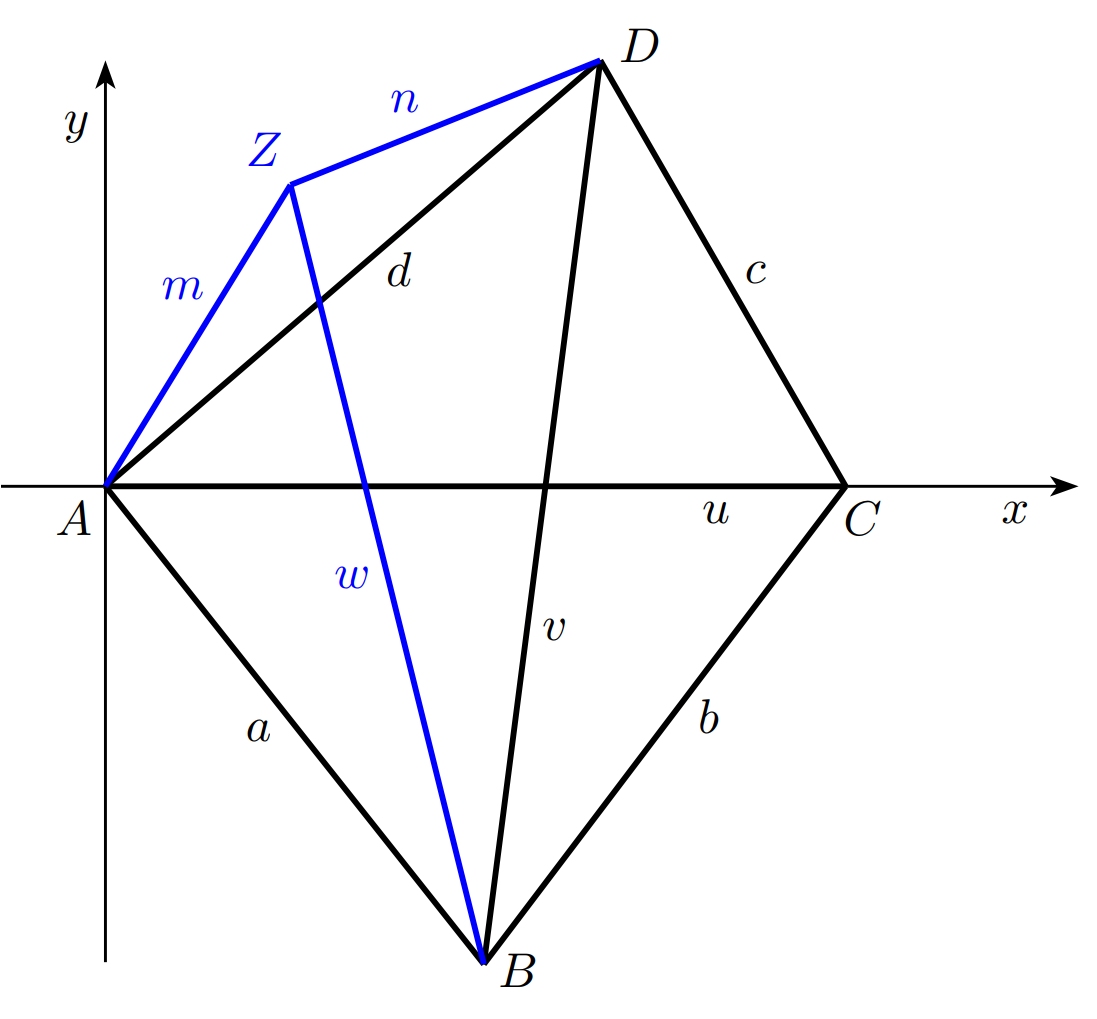
<<<<<<< HEAD Řešení. Postup bude stejný, jako v úloze 2, ale využijeme čtyřúhelník \(ABDZ\). V tomto čtyřúhelníku známe délky všech stran (délku strany \(DZ\) označme \(n\), délku strany \(ZA\) označme \(m\)) a délku úhlopříčky \(AD\). Úkolem je určit délku druhé úhlopříčky, označme ji \(w\).
Opět je výhodné dobře si zvolit souřadnou soustavu. Počátek volíme v bodě \(A\) a kladná část osy \(x\) bude obsahovat bod \(D\). Souřadnice vrcholů čtyřúhelníka v této souřadné soustavě budou \[A[0,0],\;B[b_1,b_2,\;D[d,0],\;Z[z_1,z_2].\]
Nápověda. Můžeme využít výsledků předchozí úlohy a postupovat pdoobně. V tomto případě akorát musíme pracovat s čtyřúhelníkem \(ABDZ\). Zvolíme-li souřadnou soustavu stejně jako v minulém případě, tj. počátek leží v bodě \(A\) a kladná část osy \(x\) obsahuje bod \(C\), pak dostaneme >>>>>>> 8c38db1bbe46cbb73681d7275578f27d5404274b \[ \begin{aligned} & z_1 = \frac{1}{2d}(m^2-n^2+d^2),\\ & z_2 = \sqrt{m^2-z_1^2},\\ & b_1 = \frac{1}{2d}(a^2-v^2+d^2),\\ & b_2 = -\sqrt{a^2-b_1^2}. \end{aligned} \] Odsud je možné vypočíst velikost úhlopříčky \(w\) jako délku vektoru \(\overrightarrow{BZ}\) \[w=\|\overrightarrow{BZ}\|=\sqrt{(z_1-b_1)^2+(z_2-b_2)^2}.\]
<<<<<<< HEAD
=======
8c38db1bbe46cbb73681d7275578f27d5404274b ## Odkazy a literatura