Bioróżnorodność wysp
 30 min.,
30 min.,  2/3
2/3 W tym tekście pokażemy znaczenie logarytmów w naukach biologicznych.
Życie w przyrodzie to ciągła walka o przetrwanie. Zwierzęta lub rośliny muszą zapewnić przetrwanie swojego gatunku. W przypadku zwierząt obejmuje to zdolność i siłę do ucieczki przed drapieżnikami, dostęp do pożywienia i dostępność miejsc lęgowych, rozmnażanie i ochronę potomstwa, dopóki nie będzie ono w stanie żyć samodzielnie. Aby osiągnąć ten cel, wymagana jest wystarczająca przestrzeń życiowa. Wymagania te można spełnić na obszarze z wystarczającą ilością zasobów (żywność, miejsca gniazdowania itp.). Ilość zasobów jest ściśle związana z wielkością obszaru.
Biolodzy znają prawo, które definiuje związek między liczbą gatunków stale żyjących w ekosystemie a obszarem tego ekosystemu. Ta zależność gatunek-obszar ma postać
\[N=c A^k,\tag{1}\]
gdzie \(N\) to liczba gatunków, \(A\) to powierzchnia terenu, a \(c\) i \(k\) to stałe. Stała \(c\) zależy od jednostek powierzchni i wskazuje teoretyczną liczbę gatunków na obszarze o jednostkowej wielkości. Stała \(k\) zazwyczaj waha się od \(0{,}2\) do \(0{,}35\) dla wysp i od \(0{,}12\) do \(0{,}17\) dla stałego lądu.
Zależność (1) została potwierdzona eksperymentalnie, na przykład na wyspach namorzynowych w pobliżu Florydy. Te małe wyspy są zasadniczo drzewami wyrastającymi ze słonawej wody płytkiego morza. Biorąc pod uwagę niewielkie rozmiary wyspy, możliwe było zbadanie reakcji ekosystemu na zmiany jej powierzchni. Naukowcy użyli piły łańcuchowej, aby zmniejszyć obszar i zaobserwowali odpowiedni spadek liczby gatunków. Dodatkowo przeprowadzono eksperymenty z kolonizacją niezamieszkanej wyspy. W takich przypadkach życie na wysepce było eliminowane chemicznie, podobnie jak dezynfekowane są domy. Następnie naukowcy zaobserwowali, że bogactwo gatunkowe spontanicznie powróciło do pierwotnego stanu. Co ciekawe, liczba gatunków pozostała taka sama, ale określone gatunki zostały zastąpione przez inne.
Ponieważ zależność (1) jest funkcją potęgową o wykładniku niecałkowitym, zależność między obszarem ekosystemu a liczbą gatunków nie jest łatwa do zidentyfikowania na podstawie zmierzonych lub zaobserwowanych danych. Niemniej jednak, znajomość tej zależności funkcjonalnej jest ważna. Jest ona przydatna na przykład w ochronie przyrody. Należy zauważyć, że w kontekście biogeografii wysp termin wyspa oznacza w rzeczywistości uogólnioną wyspę. Pod pojęciem wyspy nie rozumiemy tylko lądu otoczonego morzem, ale każdy obszar umieszczony na obszarze innego typu. Na przykład wyspą może być jezioro na lądzie, mały las w krajobrazie rolniczym lub obszar chronionego krajobrazu otoczony ziemią o normalnym reżimie. Wiedza o tym, w jaki sposób wielkość obszaru wiąże się ze składem gatunkowym i różnorodnością, jest ważnym czynnikiem przy podejmowaniu decyzji o budowie jednego dużego rezerwatu przyrody lub kilku małych w celu ochrony przyrody.
Prawo podobne do zależności (1) jest bardzo często spotykane w biologii w zależnościach allometrycznych. Są to zależności, w których fizyczne i fizjologiczne właściwości organizmów zmieniają się w zależności od wielkości organizmu. Na przykład zależność między czasem potrzebnym do osiągnięcia dojrzałości a masą ciała ma podobną formę, patrz Begon (1997). Innym przykładem jest prawo Kleibera, które wiąże wagę zwierzęcia z jego podstawowym metabolizmem.
W poniższych problemach rozwiążemy zadania związane ze wzorem (1) i pokażemy, jak używać logarytmów do pracy z nim.
Zadania
Zadanie 1: Weź logarytm z obu stron równania (1). Wykaż, że otrzymana zależność jest liniowa, tzn. jeśli logarytm wielkości obszaru zostanie wykreślony jako funkcja logarytmu liczby gatunków, wykres tej zależności będzie linią prostą.
Roziązanie. Zaczynamy od relacji (1), i.e., \[N=c A^k.\]
Biorąc logarytm otrzymujemy
\[\log N= \log (c A^k).\]
Korzystając z reguł logarytmowania iloczynów i potęg, otrzymujemy
\[\log N= \log (c) + k\log A.\]
Podstawienia \(y=\log N\), \(q = \log c\), \(x=\log A\) przekształcają równanie do postaci
\[y=kx+q,\]
które jest równaniem prostej o nachyleniu \(k\).
Uwaga: Ponieważ nie zawsze wygodnie jest obliczać dwa logarytmy dla każdej wartości podczas wykreślania, używane są osie logarytmiczne. Odległość punktu \(x\) od punktu 1 na osi logarytmicznej wynosi \(\log x\) i ta skala jest używana zarówno dla osi poziomej, jak i pionowej.
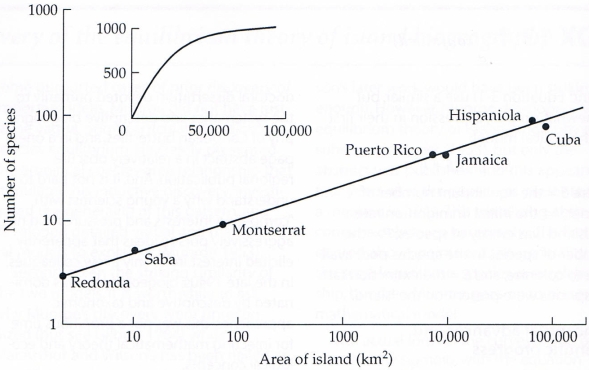
Załączony rysunek pokazuje, że wykres funkcji potęgowej w osiach logarytmicznych jest linią prostą. Wykres obejmuje liczbę gatunków gadów i płazów na wyspach w Indiach Zachodnich (Antyle i Bahamy). Na wykresie z osiami logarytmicznymi dane układają się niemal dokładnie w linię prostą. Właściwość ta jest łatwo widoczna w danych i można ją łatwo potwierdzić metodami matematycznymi. Mniejszy obrazek pokazuje, jak wyglądałaby zależność bez użycia osi logarytmicznych. Dane leżą wzdłuż krzywej i nie jest od razu jasne, czy jest to krzywa potęgowa, wykładnicza, czy jakaś inna zależność.
Zadanie 2: Szacuje się, że dla pewnego obszaru wartość wykładnika \(k\) wynosi \(0,15\). O ile zmniejszy się liczba gatunków, jeśli obszar zostanie zredukowany do jednej dziesiątej? (Ćwiczenie to modeluje na przykład ekstensywną wycinkę lasów).
Rozwiązanie. Wychodząc z prawa \[N(A)=c A^k\] i redukując powierzchnię do jednej dziesiątej, otrzymujemy \[N(0{,}1A) = c\cdot(0{,}1 A)^k = c A^k \cdot 0{,}1^k = N(A)\cdot 0{,}1^k\] Stąd, dla \(k=0{,}15\), otrzymujemy \[\frac{N(0{,}1A)}{N(A)}=0{,}1^k = 0{,}71.\] Po zmniejszeniu obszaru do jednej dziesiątej, liczba gatunków zwierząt spada do 71% stanu początkowego, czyli zmniejsza się o 29%.
Zadanie 3: Zaobserwowano, że po zmniejszeniu powierzchni do jednej czwartej liczba gatunków spadła do siedemdziesięciu procent stanu początkowego. Oszacuj wartość parametru \(k\).
Rozwiązanie. Oryginalne wartości powierzchni i liczby gatunków oznaczymy jako \(A_1\) i \(N_1\). Nowe wartości to \(A_2\) i \(N_2\). Oba zestawy danych spełniają równanie (1), zatem \[N_1 = c A_1^k\] i \[N_2 = c A_2^k.\] Dzieląc te równania, otrzymujemy \[\frac{N_1}{N_2} = \frac{c A_1^k}{ c A_2 ^k} =\left(\frac {A_1}{A_2}\right)^k.\] Zgodnie z podanym problemem, \(N_2=0{,}7N_1\) i \(A_2=0{,}25A_1\), tj, \[\frac{N_1}{0{,}7N_1}=\left(\frac{A_1}{0{,}25A_1}\right)^k\] \[\frac{1}{0{,}7}=\left(\frac{1}{0{,}25}\right)^k.\] Biorąc logarytm z obu stron, otrzymujemy \[\log\frac{1}{0{,}7}=k\cdot\log\frac{1}{0{,}25}.\] a zatem \[k=\frac{\log \frac1{0{,}7}}{\log 4}\approx 0{,}257.\]
Literatura
- Teoria biogeografii wysp, ENVI WIKI, https://www.enviwiki.cz/w/index.php?title=Teorie_ostrovn%C3%AD_biogeografie, Październik 3, 2023, (w j.czeskim)
- Czym jest biogeografia wysp?, https://zemepisec.cz/biogeografie/ostrovni/, October 3, 2023, (w j.czeskim)
- Zależność gatunek-powierzchnia, Wikipedia, https://en.wikipedia.org/wiki/Species%E2%80%93area_relationship, Październik 3, 2023
- Culek M., Biogeography, https://is.muni.cz/el/1431/jaro2010/Z0005/18118868/index_book_3-1-1.html, Październik 3, 2023, (w j.czeskim)
- Begon, M. et al. Ecology: Jednostki, populacje i społeczności: [Inwestycje w rozwój edukacji, reg.no.: CZ1.07/2.2.00/15.0084]. 1st ed. Olomouc: Wydawnictwo Uniwersytetu Palackiego, 1997. 949 p. ISBN 80-7067-695-7. (Czeskie tłumaczenie angielskiego oryginału)