Prvý Keplerov zákon hovorí:
Planéty sa pohybujú okolo Slnka po eliptických dráhach, pričom Slnko je umiestnené v jednom z ohnísk tejto elipsy.
Miesto na trajektórii, kde je Zem najbližšie (alebo najďalej) od Slnka, sa nazýva perihélium (alebo afélium). Situácia je znázornená na nasledujúcom obrázku, ktorý je zámerne zdeformovaný, aby bol eliptický tvar dráhy viditeľný. Vzdialenosti sú uvedené v miliónoch kilometrov na základe údajov z programu Stellarium a zodpovedajú roku 2022.
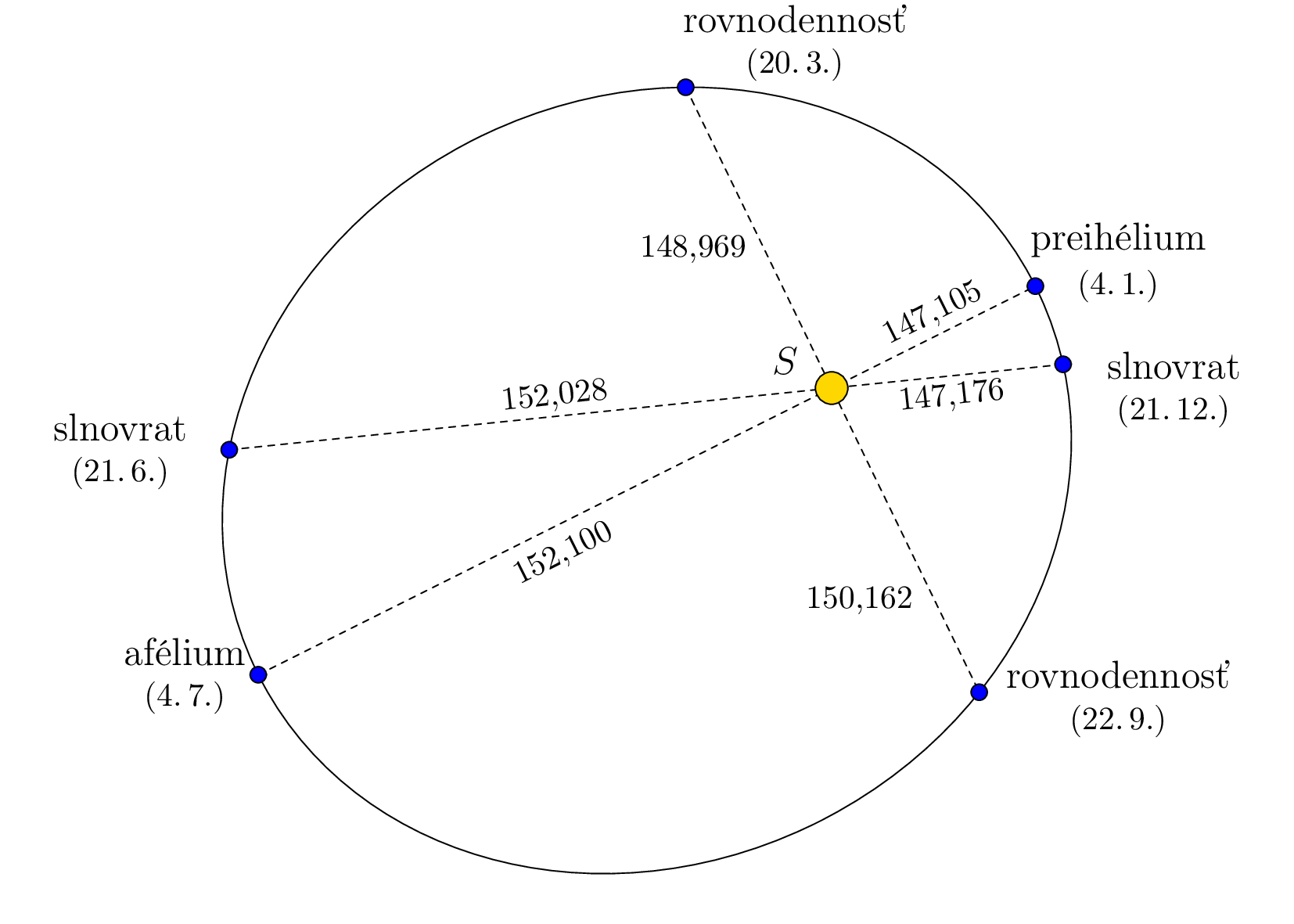
Úloha 1. Použitím informácií na obrázku určte excentricitu a dĺžky veľkej a malej polosy eliptickej trajektórie Zeme.
Riešenie. Keďže Slnko je v jednom z ohnísk elipsy, afélium a perihélium sú jej hlavnými vrcholmi. Súčet vzdialeností od Slnka k Zemi v aféliu a perihéliu je teda dvojnásobkom dĺžky veľkej polosy \(a\). A teda
\[a=\frac{152{,}100\cdot10^6\,\text{km} + 147{,}105\cdot10^6\,\text{km}}{2}\doteq149,603\cdot10^6\,\text{km}.\]
Ako je vidieť na obrázku (kde bod \(O\) predstavuje stred elipsy), rozdiel medzi vzdialenosťou od Slnka k Zemi v aféliu a dĺžkou veľkej polosy \(a\) určuje excentricitu \(e\). Teda
\[e=152,100\cdot10^6\,\text{km} - 149,603\cdot10^6\,\text{km} =2,497\cdot10^6\,\text{km}.\]
Keďže pre elipsu platí vzťah \(a^2 = b^2 + e^2\), kde \(b\) je dĺžka malej polosy, môžeme teraz určiť dĺžku malej polosy:
\[b=\sqrt{a^2 - e^2}\doteq 149,582\cdot10^6\,\text{km}.\]
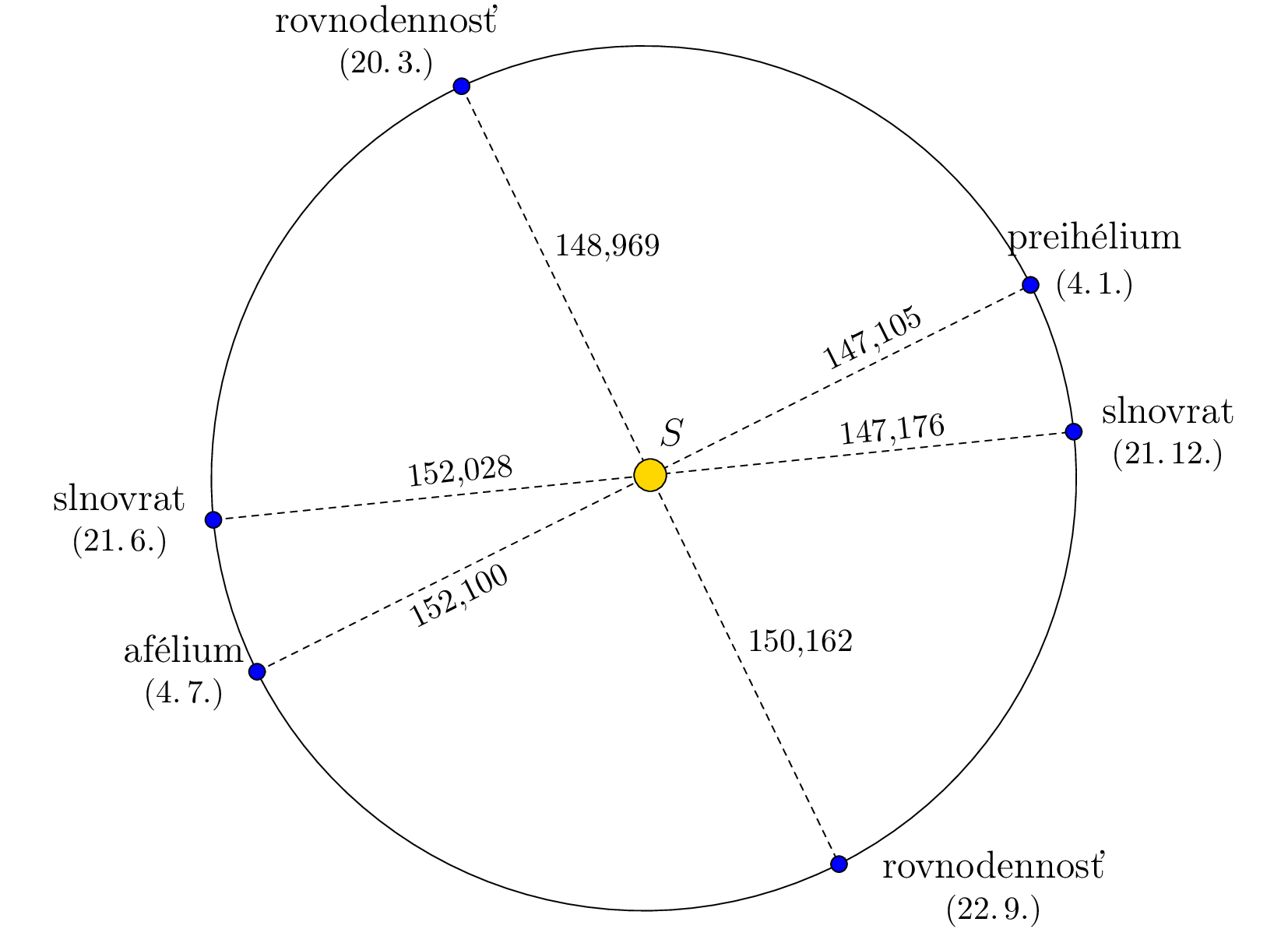
Ak teraz prekreslíme obrázok z úlohy tak, aby pomer dĺžok osí zodpovedal realite, je zrejmé, že tvar dráhy je skutočne veľmi blízky kruhu, so Slnkom v jeho strede.
