Pierwsze prawo Keplera mówi:
Planety poruszają się wokół Słońca po eliptycznych trajektoriach, a Słońce znajduje się w jednym z ich ognisk.
Punkt na trajektorii, w którym Ziemia znajduje się najbliżej (lub najdalej) Słońca nazywany jest peryhelium (lub aphelium). Sytuacja jest pokazana na poniższym rysunku, który jest celowo zniekształcony, aby widoczny był eliptyczny kształt trajektorii. Odległości podane są w milionach kilometrów, na podstawie danych z programu Stellarium i odpowiadają rokowi 2022.
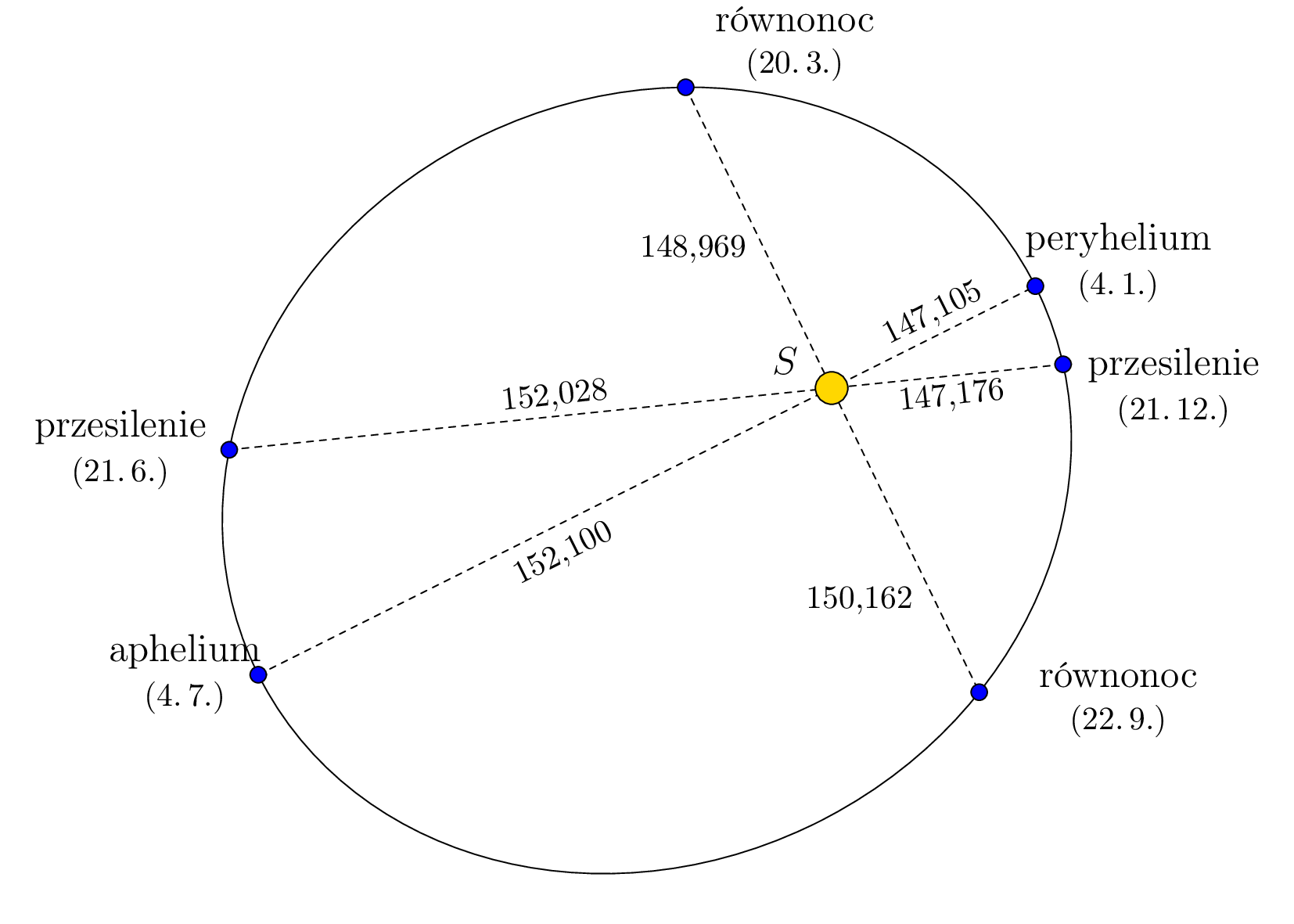
Zadanie 1. Korzystając z informacji przedstawionych na rysunku, określ mimośród oraz długości półosi głównej i półosi małej eliptycznej trajektorii Ziemi.
Rozwiązanie Ponieważ Słońce znajduje się w jednym z ognisk elipsy, aphelium i peryhelium są jej głównymi wierzchołkami. Dlatego suma odległości od Słońca do Ziemi w aphelium i peryhelium jest dwa razy większa od długości osi półcienia \(a\). Zatem,
\[a=\frac{152{,}100\cdot10^6\,\text{km} + 147{,}105\cdot10^6\,\text{km}}{2}\doteq149,603\cdot10^6\,\text{km}.\]
Jak widać na rysunku (gdzie punkt \(O\) reprezentuje środek elipsy), różnica między odległością Słońca od Ziemi w aphelium a długością półosi głównej \(a\) daje mimośród \(e\). Zatem
\[e=152,100\cdot10^6\,\text{km} - 149,603\cdot10^6\,\text{km} =2,497\cdot10^6\,\text{km}.\]
Ponieważ dla elipsy zachodzi zależność \(a^2 = b^2 + e^2\), gdzie \(b\) jest długością osi półminimalnej, możemy teraz określić długość osi półminimalnej:
\[b=\sqrt{a^2 - e^2}\doteq 149,582\cdot10^6\,\text{km}.\]
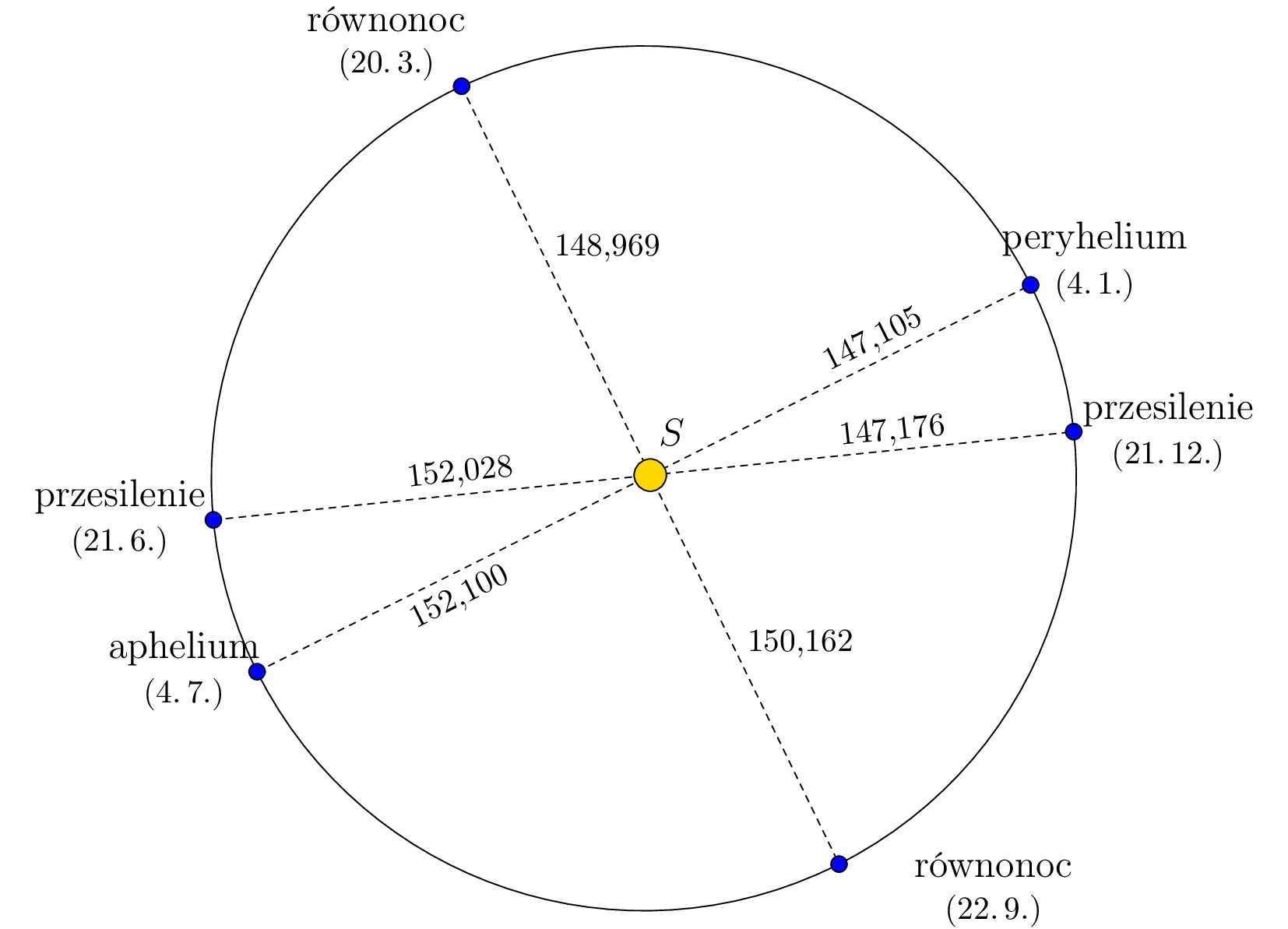
Jeśli teraz przerysujemy figurę z ćwiczenia tak, aby stosunek długości osi odpowiadał rzeczywistości, okaże się, że kształt trajektorii jest rzeczywiście bardzo zbliżony do okręgu, ze Słońcem w środku.
