Pokrok v oblasti elektrotechniky umožnil vývoj nových navigačných systémov založených na prenose elektromagnetických vĺn. Príkladom takéhoto systému je námorná navigácia LORAN-C , ktorá bola vyvinutá počas druhej svetovej vojny v USA. V tomto type navigácie prijíma plavidlo synchronizovaný signál od dvojice vysielačov. Signál od vzdialenejšieho vysielača je prijatý plavidlom neskôr, takže oneskorenie signálu určuje rozdiel medzi vzdialenosťami plavidla od prvého a druhého vysielača.
Množina bodov, ktoré majú konštantný rozdiel vo vzdialenostiach od dvoch daných pevných bodov, je hyperbola. Plavidlo sa teda nachádza na hyperbole, ktorej ohniskami sú vysielače, a ktorá je určená rozdielom vzdialeností plavidla od týchto vysielačov. Oneskorenie signálu od ďalšej dvojice staníc potom určuje druhú hyperbolu, na ktorej sa plavidlo musí nachádzať. Ak sa plavidlo nachádza na oboch hyperbolách, nachádza sa v ich priesečníku.
Úloha 1. V krajine sú umiestnené tri vysielače \(P_1\), \(P_2\) a \(P_3\). Obrázok zachytáva vzdialenosti, ktoré poznáme: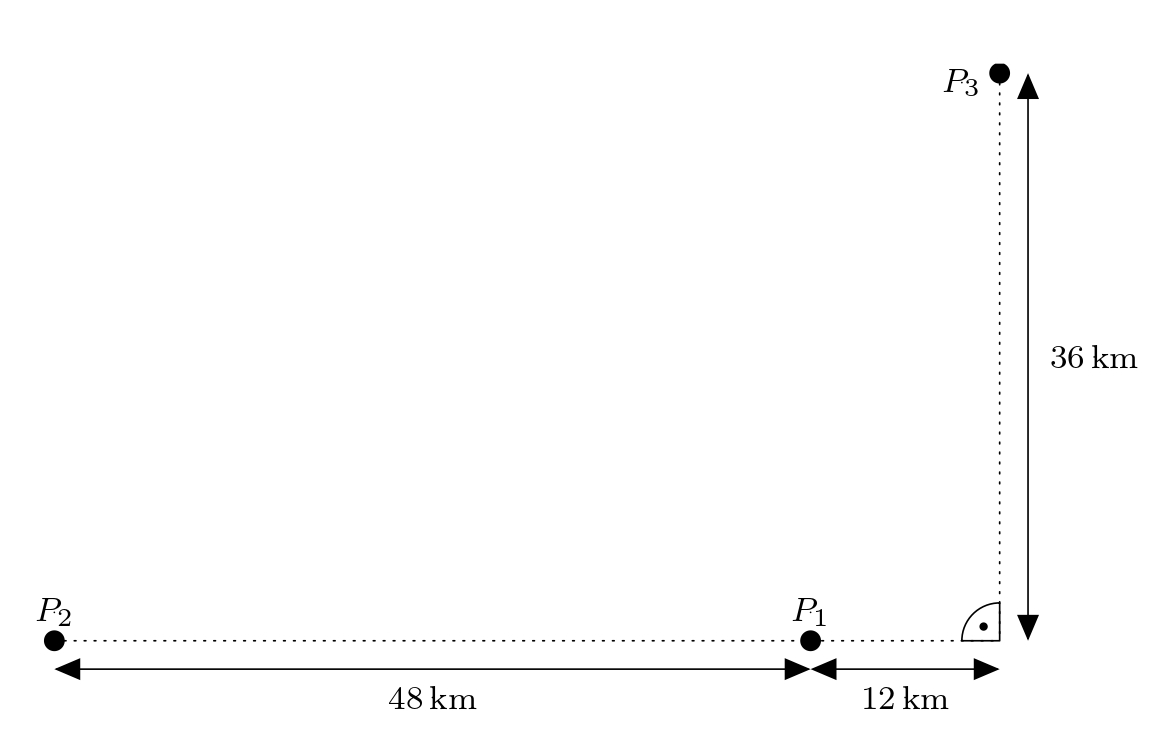 
Adamova turistická navigácia pošle signál do všetkých troch prijímačov. Signál dorazí do prijímačov \(P_1\) a \(P_3\) v rovnakom čase a do prijímača \(P_2\) o 80 mikrosekúnd neskôr. Kde sa Adam nachádza? Predpokladajte, že signál sa šíri rýchlosťou 300 000 km za sekundu. Určte polohu vo vhodne zvolenom súradnicovom systéme.
Riešenie. Najprv na obrázku vyberieme vhodný karteziánsky súradnicový systém. Tento výber odôvodníme nasledovne: Keďže Adam je rovnako vzdialený od prijímačov \(P_1\) a \(P_3\), nachádza sa na osi úsečky \(P_1P_3\). Skutočnosť, že jeho signál dorazí do prijímača \(P_2\) o 80 mikrosekúnd neskôr ako do prijímača \(P_1\), znamená, že Adam je o \(24\,\text{km}\) ďalej od prijímača \(P_2\) než od prijímača \(P_1\). Jeho poloha je preto tiež na vetve hyperboly \(h\) s ohniskami \(P_1\) a \(P_2\), kde rozdiel vzdialeností Adama od \(P_1\) a \(P_2\) je práve \(24\,\text{km}\). Je výhodné umiestniť začiatok súradnicového systému do stredu úsečky \(P_1P_2\), aby rovnica hyperboly \(h\) mala čo najjednoduchšiu formu. Označme začiatok sústavy súradníc ako \(O\) a umiestnime ho do stredu úsečky \(P_1P_2\). Kladný smer osi \(x\) bude určený polpriamkou \(OP_1\) a kladný smer osi \(y\) zvolíme tak, aby druhá súradnica bodu \(P_3\) bola kladná. Keďže všetky dané rozmery sú násobky \(12\), zvolíme jednotky na oboch osiach tak, aby zodpovedali vzdialenosti \(12\,\text{km}\). Situácia je znázornená na obrázku: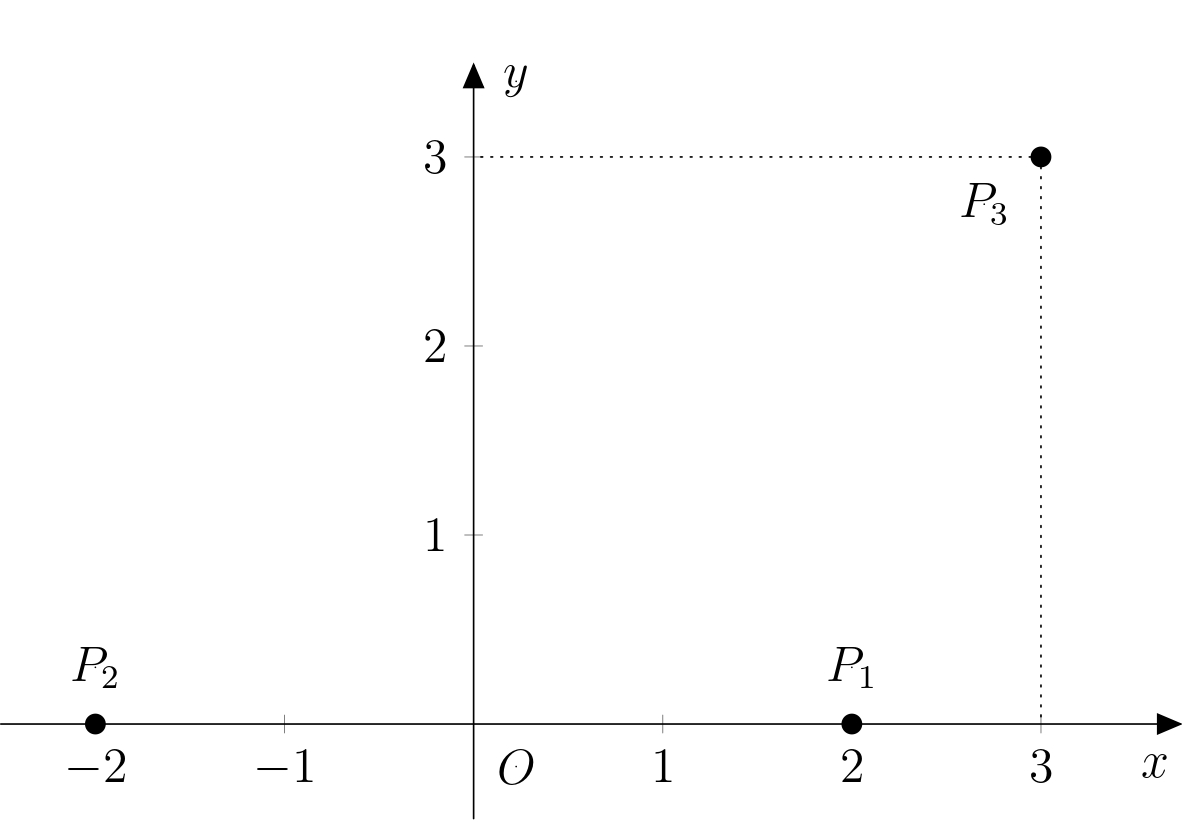 
Nech \(A\) označuje neznámu polohu Adama. Vieme, že bod \(A\) leží na osi úsečky \(P_1P_3\). Túto os (označme ju \(o\)) vyjadríme parametricky: \[o\colon X = S_{P_1P_3}+t\cdot \overrightarrow{u_o},\] kde \(S_{P_1P_3}\left[\frac{5}{2};\frac{3}{2}\right]\) a \(\overrightarrow{u_o}=(3;-1)\). Potom \[ \begin{aligned} x &= \tfrac{5}{2} + 3t\\ y &= \tfrac{3}{2} - t,\quad t\in\mathbb{R}. \end{aligned} \] Na nájdenie rovnice hyperboly si všimnime, že body \(P_1\) a \(P_2\) sú ohniská hyperboly \(h\), so stredom v bode \(O\) a excentricitou \(e\) rovnajúcou sa polovici vzdialenosti \(|OP_1|\), teda \(e=2\). Ďalej, keďže rozdiel \(|AP_1| - |AP_2| = 2\) je dvojnásobkom dĺžky veľkej polosi hyperboly, dĺžka veľkej polosi \(a\) je rovná \(1\). Dĺžku malej polosi \(b\) vypočítame dosadením do vzťahu \(b = \sqrt{e^2 - a^2} = \sqrt{4 - 1} = \sqrt{3}\). Teraz môžeme zapísať rovnicu požadovanej hyperboly \[h\colon x^2-\frac{y^2}{3}=1.\] Bod \(A\) leží na jej pravej vetve (je bližšie k prijímaču \(P_1\)), teda jeho prvá súradnica musí byť nutne \(x_A > 0\). Teraz vypočítajme súradnice priesečníkov priamky \(o\) a hyperboly \(h\). Dosadením parametrických rovníc priamky \(o\) do rovnice hyperboly dostaneme: \[ \begin{aligned} \left(\frac{5}{2} + 3t\right)^2-\frac{\left(\frac{3}{2}-t\right)^2}{3} &= 1 \\ 3\cdot \left(\frac{5}{2} + 3t \right)^2-\left(\frac{3}{2}-t\right)^2 &= 3 \\ \vdots & \\ 52 t^2 +96t +27 &= 0 \end{aligned} \] Koreňmi tejto kvadratickej rovnice sú \(t_1 = -\frac{9}{26}\) a \(t_2 = -\frac{3}{2}\). Dosadíme \(t_1\) do parametrických rovníc a dostaneme: \[ \begin{aligned} x_1 &= \tfrac{5}{2} + 3\cdot \left(-\tfrac{9}{26}\right) = \tfrac{19}{13}\\ y_1 &= \tfrac{3}{2} - \left(-\tfrac{9}{26}\right) = \tfrac{24}{13}, \end{aligned} \] Teda \(A_1\left[ \tfrac{19}{13};\tfrac{24}{13} \right]\). Podobne, dosadením \(t_2\) dostaneme: \[ \begin{aligned} x_2 &= \tfrac{5}{2} + 3\cdot \left(-\tfrac{3}{2}\right) = -2\\ y_2 &= \tfrac{3}{2} - \left(-\tfrac{3}{2}\right) = 3, \end{aligned} \] Teda \(A_2 \left[ -2;3 \right]\). Avšak bod \(A_2\) nespĺňa podmienku \(x_A > 0\) (nachádza sa na druhej vetve hyperboly), takže dostávame jedinú možnú polohu Adama, a to \(A\left[ \tfrac{19}{13};\tfrac{24}{13} \right]\). Riešenie je znázornené na obrázku.
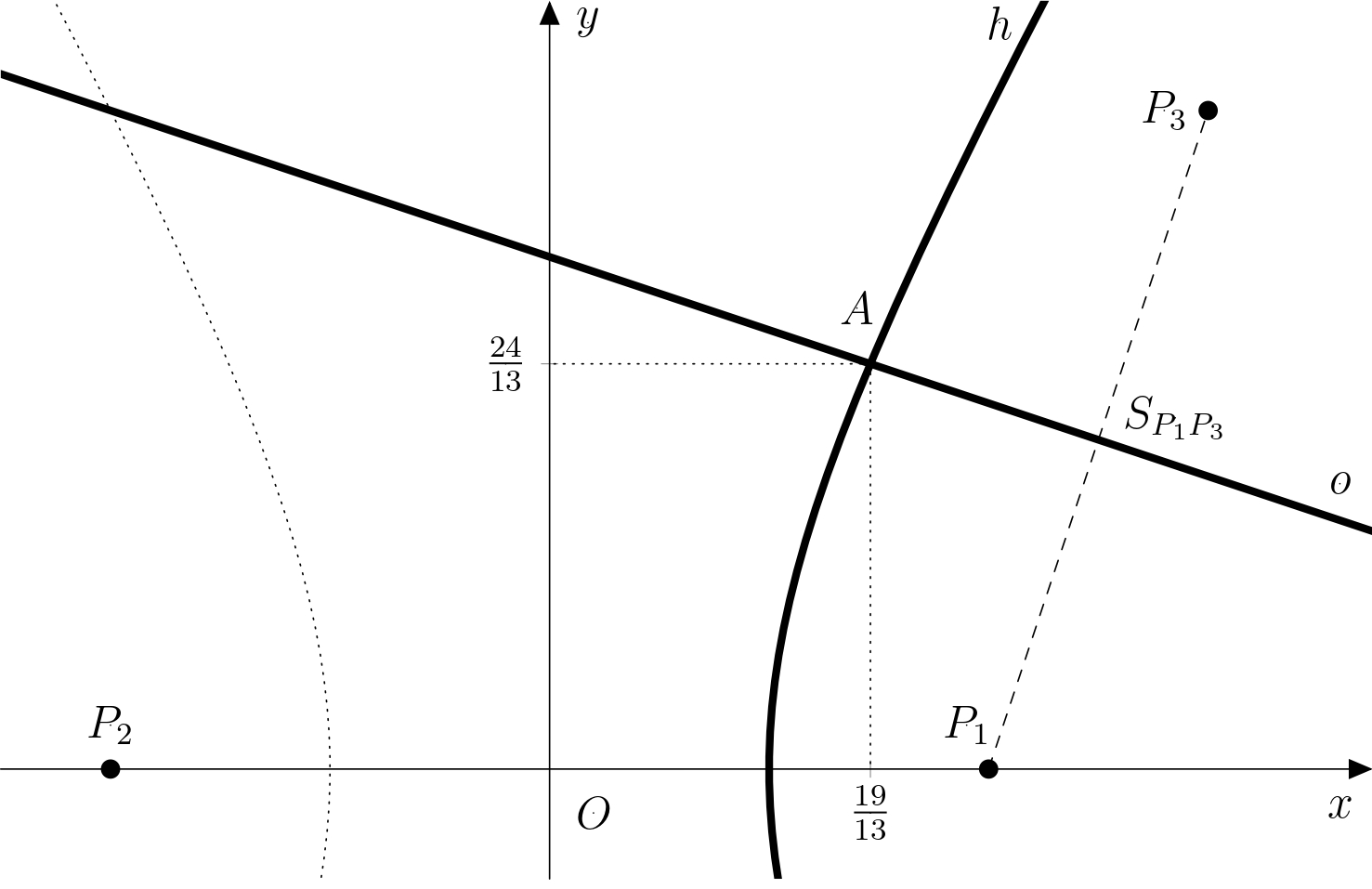
Poznámka Ak by Adam nebol rovnako vzdialený od prijímačov \(P_1\) a \(P_3\), riešenie problému by znamenalo nájsť priesečník vetiev dvoch hyperbol. Takýto výpočet by však presahoval rámec stredoškolskej matematiky.