Tomógrafo acústico y ecuación de la elipse

15 min., 1/3

Imagina que necesitas evaluar la salud de un árbol viejo sin tener que talarlo. La tecnología moderna te permite hacerlo de forma suave pero precisa, y una de las herramientas clave es la ecuación de la elipse. Utilizando el método EBSI (elliptise-based spatial interpolation) puedes estimar las propiedades físicas de la madera dentro del tronco a partir de los datos medidos y así obtener una idea de su resistencia y salud. Sin embargo, para ello, necesitas poder manejar la ecuación de la elipse incluso cuando esta se encuentra en una posición general respecto a los ejes. En tal caso utilizaremos el producto escalar para hallar la proyección del vector en la dirección deseada.

Tomógrafo acústico

En la práctica de un arborista, especialista en el cuidado de árboles fuera del bosque, una tarea frecuente es evaluar la vitalidad y la salud de un árbol. Esto debe realizarse con mínima o nula intervención que no afecte significativamente su estado. Uno de los pocos métodos invasivos es el uso de un tomógrafo acústico. Este dispositivo mide el tiempo de vuelo de una señal sonora (el término inglés time of flight, TOF) entre dos sensores. Mediante métodos de geometría analítica, es posible determinar la distancia entre los sensores y, asumiendo la propagación de la señal sonora en rayos directos determinar la velocidad de propagación del sonido en el material. Este valor es un indicador muy importante de las propiedades físicas y mecánicas, ya que el sonido se propaga más rápido en madera sana (en inglés sound wood) que en madera degradada (en inglés degraded wood).

Problemas de reconstrucción de imágenes

La reconstrucción de imágenes en un tomógrafo acústico se basa en la suposición de la propagación directa de los rayos en la sección del tronco. Por lo tanto, no se tienen en cuenta las reflexiones ni la refracción de las ondas. La calidad de esta suposición es objeto de investigación científica actual; sin embargo, una suposición de este tipo es necesaria para el uso práctico del método.

Dado que se basa en un número relativamente pequeño de rayos (un tomógrafo acústico suele tener 12, como máximo 24 sensores, e incluso menos para árboles de diámetro pequeño), es necesario utilizar algún método de interpolación y promediación. Esto diferencia la tarea, por ejemplo, de la de los tomógrafos utilizados en el ámbito sanitario, donde hay un orden de magnitud mayor de rayos de imagen y la geometría de medición también está mejor definida: las fuentes y los sensores se colocan, por ejemplo, alrededor de la circunferencia de un círculo y no alrededor de la circunferencia irregular del tronco de un árbol. Para eliminar las deficiencias asociadas con el uso de un tomógrafo acústico para árboles, se han desarrollado diversas técnicas que permiten la interpolación y el promediado de los valores medidos.

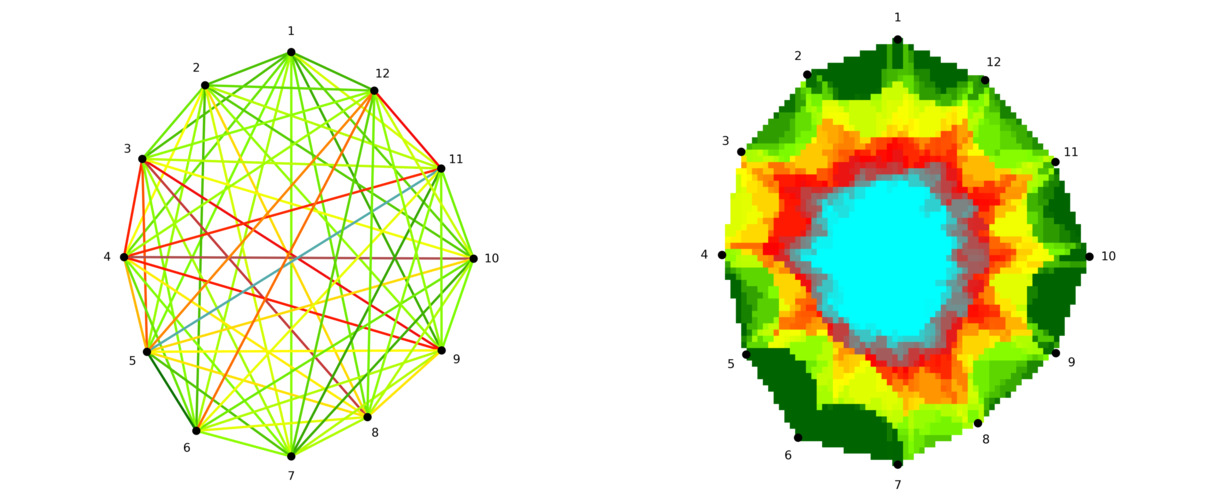
El método EBSI y sus seguidores

Muchos métodos de reconstrucción de imágenes en tomógrafos acústicos se basan en la suposición de que la velocidad de propagación del sonido se ve afectada por la calidad de la madera en el entorno elíptico de la línea de conexión entre dos sensores. Esta suposición se probó con mediciones reales v Du et al. (2015), donde se propuso una fórmula que relaciona la distancia entre sensores y la excentricidad de la elipse. Este enfoque obtuvo mejores resultados que los métodos basados ​​en la simple intersección de rayos y el promedio de las velocidades en estas intersecciones. El método se denominó Ellipse-based spatial interpolation y se abrevió como EBSI.

La implementación práctica del método de reconstrucción de imágenes consiste en dividir la sección transversal del tronco en celdas individuales, en las que se promedian los valores medidos. En el método EBSI, para cada celda, la velocidad se determina como el promedio de las velocidades de todos los rayos en cuya vecindad elíptica se encuentra la celda.

En otros trabajos, el método EBSI se amplió. Alrededor de cada rayo, se considera nuevamente una elipse que define su área de aplicación (véase la Figura 3). Los datos se procesan en dos rondas utilizando los métodos RSEN y SISE (del inglés ray sementation by elliptical neighborhood a spatial interpolation by segmented ellipse) descritos en Du et al (2018).

Se puede encontrar una descripción detallada de los métodos en la bibliografía original, sin embargo, incluso a partir de la descripción simplificada anterior queda claro que una subtarea fundamental en la implementación de la reconstrucción de imágenes es verificar si un punto en el plano se encuentra dentro de la elipse o fuera de ella.

Ecuación de una elipse

De la motivación anterior se desprende que, para la implementación práctica de la reconstrucción de imágenes mediante el método EBSI, es necesario trabajar eficazmente con la elipse en diversas posiciones, lo que incluye la rotación arbitraria de los ejes y el desplazamiento arbitrario del centro de la elipse. Necesitamos determinar eficazmente si un punto se encuentra dentro o fuera de la elipse.

Una elipse es un conjunto de puntos en un plano para el cual la suma de las distancias de un punto a sus dos focos es constante. Una elipse se puede definir utilizando los ejes mayor y menor. Consideremos una elipse con la longitud del semieje mayor \(a\) y la longitud del semieje menor \(b\). La ecuación de una elipse con centro en el origen del sistema de coordenadas y el eje mayor en la dirección del eje \(x\) tiene la forma: \[ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1. \] Los puntos que se encuentran dentro de la elipse satisfacen entonces la desigualdad: \[ \frac{x^2}{a^2}+\frac{y^2}{b^2}<1. \] Sin embargo, trabajamos con elipses en posición general; sus ecuaciones pueden transformarse a la misma forma, pero este proceso es bastante laborioso y, para nuestros propósitos, innecesario. En lugar de trabajar con coordenadas, usaremos las distancias de un punto a los semiejes mayor y menor. Si la elipse tiene la ecuación anterior, estas distancias son directamente las coordenadas \(x\) y \(y\) del punto.

Por lo tanto, si \(d_1\) es la distancia de un punto a la línea definida por el eje menor (para abreviar, la distancia desde el eje menor) y la distancia de un punto al eje mayor es \(d_2\), entonces el punto se encuentra dentro de la elipse si y sólo si \[ \frac{d_1^2}{a^2}+\frac{d_2^2}{b^2}<1.\tag{1} \] Para verificar si un punto se encuentra dentro de la elipse, es suficiente determinar la distancia del punto a los ejes mayor y menor y verificar la validez de la desigualdad anterior (1).

Longitud de proyección de un vector y el producto escalar

La figura muestra los ejes mayor y menor de la elipse, los vectores unitarios en la dirección de estos ejes, la línea que conecta el punto probado con el centro de la elipse y las distancias del punto desde los ejes individuales de la elipse.

Para simplificar, supongamos que el ángulo entre los vectores \(\vec u\) y \(\vec e_1\) es agudo. A partir de la definición del producto escalar y del hecho de que el vector \(\vec e_1\) es un vector unitario, tenemos

\[\vec u\cdot\vec e_1 = |\vec u||\vec e_1|\cos\varphi = |\vec u| \cos\varphi = d_1.\]

Por lo tanto, la distancia desde el eje menor se puede determinar mediante el producto escalar. La proyección perpendicular de un vector sobre una línea se denomina proyección, y en la figura se puede observar que \(d_1\) es es en realidad la longitud de la proyección del vector \(\vec u\) en la dirección determinada por el vector \(\vec e_1\). Si el ángulo entre los vectores \(\vec u\) y \(\vec e_1\) es obtuso, el valor \(d_1\) es negativo, pero esto no se refleja en el criterio de prueba (1).

Analogicky, délka projekce vektoru \(\vec u\) en la dirección definida por el vector \(\vec e_2\) está dada (excepto por el posible signo, que nuevamente no se refleja en la prueba (1)) por

\[d_2=\vec u\cdot \vec e_2.\]

Nota. Tenga en cuenta que el cálculo del producto escalar se realiza utilizando coordenadas según la fórmula

\[\vec u\cdot\vec v = u_1v_1+u_2v_2,\]

donde \(\vec u = (u_1, u_2)\) y \(\vec v=(v_1,v_2)\). Este cálculo se puede realizar muy rápidamente en computadoras y, mediante técnicas de programación adecuadas (vectorización), se puede realizar simultáneamente para miles de puntos, con una velocidad cien veces mayor que utilizando un ciclo basado en pruebas sucesivas de puntos individuales.

Nota. El vector unitario \(\vec e_1\) en la dirección del eje principal se puede determinar como el cociente del vector del centro al vértice principal y la longitud de este vector, o bien por el ángulo que forma el eje principal con el eje \(x\). Si este ángulo es \(\alpha\), el vector unitario viene dado por

\[\vec e_1=(\cos\alpha, \sin\alpha).\]

El vector unitario en la dirección del eje menor es perpendicular a \(\vec e_1\) Por lo tanto, es posible tomar, por ejemplo,

\[\vec e_2 = (-\sin\alpha, \cos\alpha).\]

Ejemplo de uso

Solución. El vector unitario con la dirección del eje principal es \(\vec e_1=(\cos 30^\circ, \sin 30^\circ)\). El vector \(\vec u\) está dado por las coordenadas del punto \(X\), es decir, \(\vec u=(1{,}6;1{,}6)\). Por lo tanto, el producto escalar es

\[d_1=\vec u\cdot \vec e_1 = 1{,}6\cdot\cos 30^\circ + 1{,}6\cdot\sin 30^\circ\doteq 2{,}186.\]

De manera similar, la longitud de la proyección en la dirección del eje menor dada por el vector \(\vec e_2=(-\sin 30^\circ,\, \cos 30^\circ)\) es

\[d_2=\vec u\cdot \vec e_2 = -1{,}6\cdot\sin 30^\circ + 1{,}6\cdot\cos 30^\circ \doteq 0{,}586.\]

Se aplica

\[ \frac{d_1^2}{a^2} + \frac{d_2^2}{b^2} \doteq 0{,}683<1. \]

Por lo tanto, el punto se encuentra dentro de la elipse. La situación se muestra en la siguiente figura.

Conclusión

El texto presentó los pasos básicos en los que se basa la reconstrucción de imágenes en un tomógrafo acústico. Una de las subtareas consiste en verificar si el punto examinado se encuentra dentro o fuera de una elipse, cuya posición general está dada por sus semiejes. Para esta verificación, resulta ventajoso utilizar la ecuación de la elipse, basada no en coordenadas, sino en distancias a los ejes mayor y menor. Esta distancia puede determinarse mediante el producto escalar de vectores.

Bibliografía y fuentes de las imágenes

Bibliografía

1. Du, X., Li, S., Li, G., Feng, H., and Chen, S. (2015). “Stress wave tomography of wood internal defects using ellipse-based spatial interpolation and velocity compensation,” BioRes. 10(3), 3948-3962. http://doi.org/10.15376/biores.10.3.3948-3962
2. Du, X.; Li, J.; Feng, H.; Chen, S. Image Reconstruction of Internal Defects in Wood Based on Segmented Propagation Rays of Stress Waves. Appl. Sci. 2018, 8, 1778. https://doi.org/10.3390/app8101778

Fuentes de las imágenes

1. Projekt DYNATREE – Tree Dynamics: Understanding of Mechanical Response to Loading, https://starfos.tacr.cz/cs/projekty/LL1909.
2. Vlastní obrázky