Cuando el tomógrafo acústico se encuentra con el resistógrafo
 15 min.,
15 min.,  1/3
1/3 Aunque no lo parezca, la geometría analítica contribuye al control del estado de salud de los árboles. Los árboles desempeñan un papel insustituible en el entorno urbano. Sin embargo, a menudo puede resultar difícil evaluar su estado de salud, especialmente cuando no hay signos externos evidentes de daño. La geometría analítica ofrece una forma eficaz de combinar diferentes métodos de diagnóstico y crear un modelo unificado que permita evaluar mejor el riesgo de caída de un árbol. Esto permite tomar decisiones más informadas sobre el cuidado y las posibles intervenciones.
La problemática de los árboles en las zonas urbanizadas
Los árboles son un elemento importante que hace que la vida en las zonas urbanas sea más agradable. Proporcionan sombra y oxígeno, reducen el polvo y el ruido, disminuyen la temperatura del entorno y ofrecen refugio para aves y otros animales.
Sin embargo, plantar árboles en zonas urbanas conlleva riesgos. Uno de los riesgos más graves es la caída de un árbol. La caída de un árbol puede causar lesiones personales, daños materiales y, en el peor de los casos, la muerte. Por lo tanto, es importante revisar periódicamente el estado de salud de los árboles y detectar cualquier problema a tiempo.
Diagnóstico de árboles
Los arboristas, expertos en el cuidado de árboles fuera del bosque, utilizan diversos métodos para diagnosticar la salud de los árboles. Estos métodos incluyen, por ejemplo, la tomografía acústica, que permite evaluar el estado de la madera del tronco de un árbol de forma no invasiva, sin necesidad de dañarlo. Se trata de un tipo de examen por TC de árboles que permite detectar defectos ocultos y degradación de la madera. A diferencia de los exámenes médicos por TC, la tomografía acústica utiliza ondas sonoras de larga longitud de onda, sujetas a limitaciones debido a los principios físicos de propagación de las ondas. Una de las consecuencias es que la tomografía acústica no permite distinguir con suficiente certeza entre un árbol con una cavidad y uno con una grieta. Ambos defectos aparecen al examinarse con una tomografía como un lugar donde el sonido se propaga más lentamente que en la madera sana circundante. Sin embargo, el tamaño de la grieta a menudo se sobreestima y puede parecer similar a una cavidad. Por lo tanto, al inspeccionar árboles, es recomendable utilizar otros métodos complementarios que permitan obtener información más completa sobre la salud del árbol.
Uno de estos métodos es el resistógrafo, que mide la rigidez de la madera y ayuda a revelar defectos ocultos. Un resistógrafo es un dispositivo que utiliza un taladro y mide la resistencia de la madera para evaluar su estructura y propiedades mecánicas. Debido a que el taladro es muy delgado, este método es relativamente poco invasivo y no daña el árbol. Un resistógrafo puede detectar grietas, cavidades y otros defectos en la madera, y los datos obtenidos de esta manera pueden utilizarse para complementar la información obtenida con un tomógrafo acústico.
En la práctica, el diagnóstico de árboles suele consistir primero en tomar mediciones con un tomógrafo acústico, que proporciona información básica sobre el estado de la madera del tronco. Posteriormente, se toman mediciones con un resistógrafo, que permite obtener información adicional sobre el estado de la madera y detectar cualquier defecto oculto. De esta forma es posible obtener una visión completa del estado de salud del árbol y detectar cualquier problema a tiempo.
La siguiente figura muestra los posibles resultados de un tomógrafo acústico y un resistógrafo. La figura de la izquierda es una reconstrucción de una imagen de un tomógrafo acústico que muestra la velocidad de propagación del sonido en la madera. Nos interesa esta velocidad porque está directamente relacionada con las propiedades mecánicas de la madera. Las áreas azul y roja representan los lugares donde el sonido se propaga más lentamente, mientras que el área verde representa los lugares donde el sonido se propaga más rápidamente. A la derecha se muestra el resultado de un resistógrafo, que muestra la potencia necesaria para mantener una velocidad de perforación constante y también es una medida de la resistencia mecánica de la madera. La perforación se realizó siempre entre dos sensores del tomógrafo acústico, de modo que se realizaron doce orificios resistográficos entre doce sensores del tomógrafo.
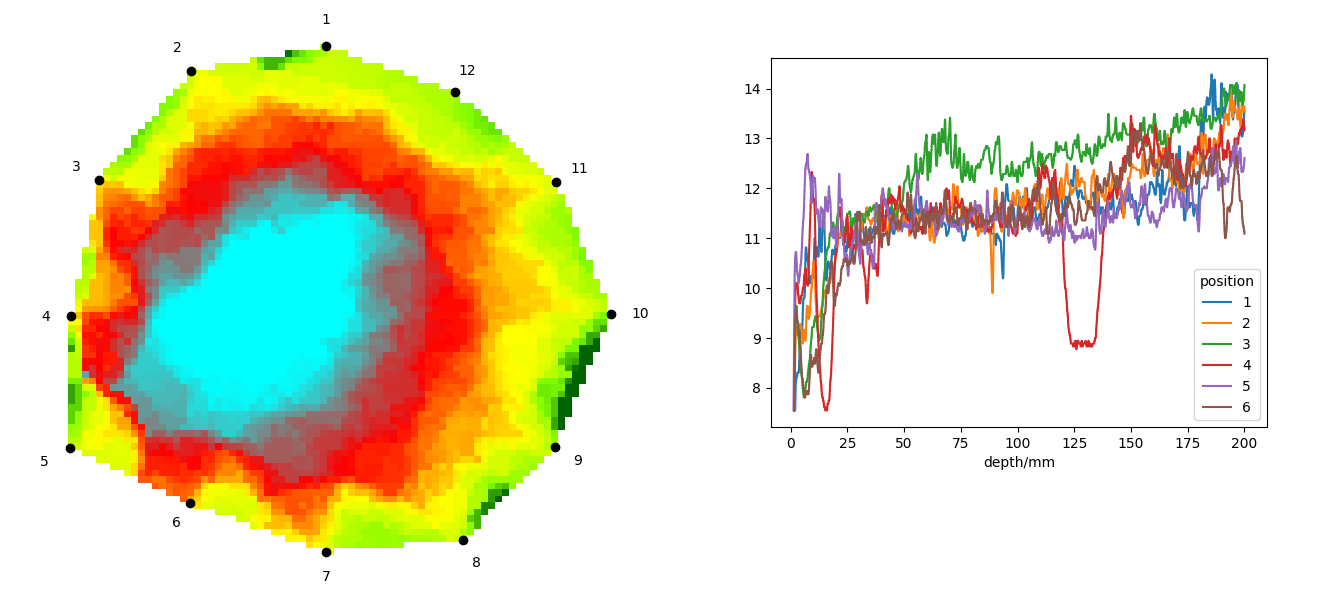
En la figura, observamos que una de las curvas del resistógrafo presenta una caída notable a una profundidad de aproximadamente 125 milímetros. Esta caída corresponde a una cavidad de aproximadamente un centímetro, pero el tomógrafo acústico muestra una cavidad mayor. Para facilitar el procesamiento de los datos, conviene combinarlos en una sola imagen. Por lo tanto, queremos mostrar las posiciones de los pozos y los datos del resistógrafo en el tomograma (resultado del tomógrafo acústico).
Combinando datos de un tomógrafo acústico y un resistógrafo
Al combinar los datos de ambos métodos, entran en juego las matemáticas. Supongamos que la perforación se realizó desde el centro de la línea que conecta dos sensores adyacentes y se dirigió hacia el centro del tronco del árbol. Representaremos los valores del resistógrafo en intensidad de gris y la imagen resultante será una composición del tomograma y una columna con intensidad de gris variable.
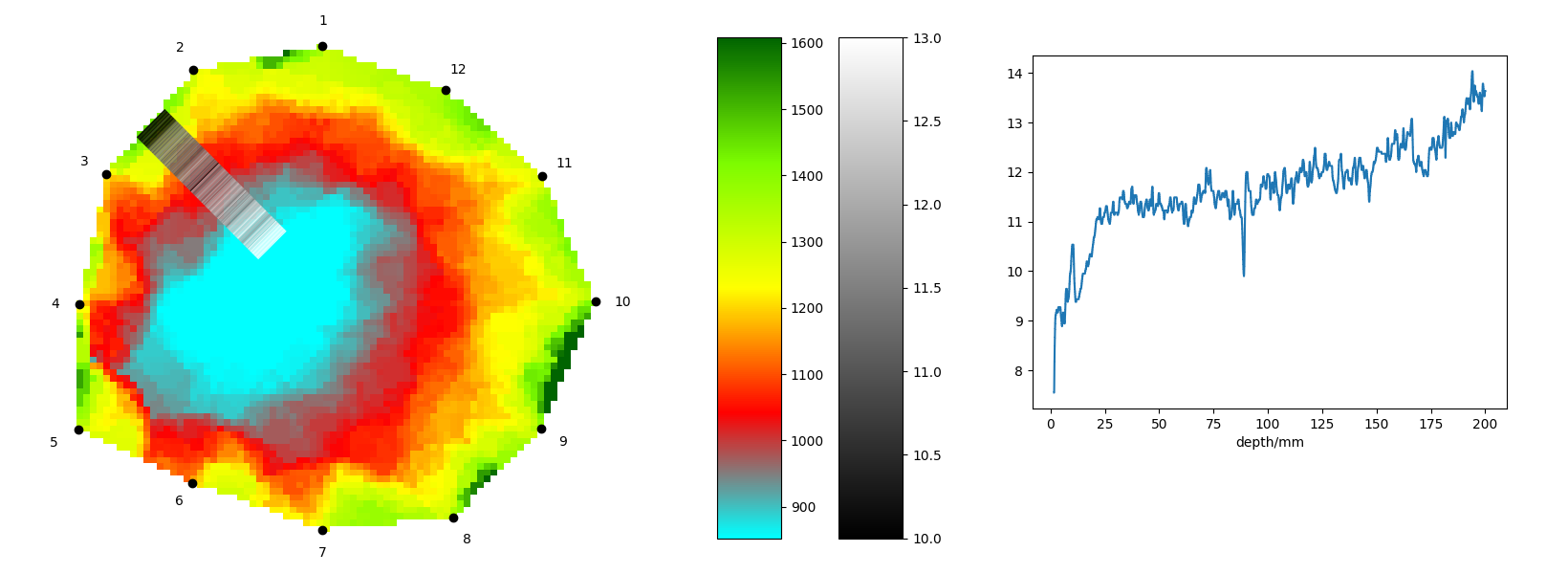
El tomograma se suele colocar en el sistema de coordenadas de modo que su centro se encuentre en el origen, el primer sensor se encuentre en el lado positivo del eje \(y\) y los demás sensores se numeren en sentido antihorario. Para crear una columna con datos del resistógrafo entre el segundo y el tercer sensor desde un punto de vista matemático, es necesario conocer la función que convierte la profundidad de la curva del resistógrafo (depth) a una posición en el sistema de coordenadas asociada al tomograma. La gráfica de dicha función será una línea recta que va desde el centro de la línea de conexión del sensor hasta el centro del árbol. Denominemos esta línea \(p\).
Los pasos individuales para encontrar ecuaciones adecuadas de la línea \(p\) pueden ser los siguientes.
- Primero, determinamos las coordenadas del centro de la línea del sensor. Lo denotaremos como \(A\). La línea buscada \(p\) pasará por el punto \(A\).
- A continuación, determinamos el vector de dirección \(\vec u\) de la línea \(p\). Este será el vector que dirigirá desde el punto \(A\) hasta el origen del sistema de coordenadas.
- Utilizando el punto \(A\) y el vector de dirección \(\vec u\) es posible escribir una ecuación paramétrica de la línea \(p\). Sin embargo, esto tendría la desventaja de que sería necesario encontrar una conexión entre este parámetro y la profundidad del pozo. No obstante, si convertimos el vector de dirección \(\vec u\) a un vector de longitud unitaria, el parámetro de la ecuación de la línea corresponderá a la profundidad del pozo. Por lo tanto, primero encontramos el vector \(\vec e\) como un vector unitario en la dirección del vector \(\vec u\).
- La ecuación paramétrica de la línea dada por el punto \(A\) y el vector \(\vec e\) define la correspondencia de la profundidad del pozo con las coordenadas del sistema de coordenadas del tomograma y puede utilizarse para complementar el tomograma con datos del resistógrafo.
Probemos este procedimiento en un ejemplo específico, que se relaciona con la geometría de la Figura 1.
Tarea 1. Las coordenadas de los puntos donde se ubicaron los sensores 2 y 3 del tomógrafo acústico son \(P_2=[-15, 26]\) y \(P_3=[-25, 14]\). Las coordenadas del centro del tomograma son \(O=[0, 0]\).
Encuentra la expresión paramétrica de la recta \(p\) que pasa por el punto \(A\) y el centro del tomograma \(O\), en la que el valor del parámetro será igual a la profundidad del pozo.
Solución. El punto medio \(A\) del segmento de línea entre los puntos \(P_2\) y \(P_3\) se calcula utilizando la relación
\[ A = \frac{P_2 + P_3}{2}.\]
Después de sustituir las coordenadas, obtenemos \(A=[-20, 20]\).
El vector de dirección \(\vec u\) de la recta \(p\) se determina utilizando los puntos \(O\) y \(A\), por los que pasa la recta \(p\) como \[\vec u = O-A,\] en las coordenadas \(\vec u = [0,0] - [-20, 20] = (20, -20)\).
La longitud del vector \(\vec u=(u_1, u_2)\) es, según el teorema de Pitágoras \[|\vec u| = \sqrt{u_1^2 + u_2^2} = \sqrt{20^2 + (-20)^2} = \sqrt{800} = 20\sqrt{2}.\]
El vector unitario \(\vec e\) en la dirección del vector \(\vec u\) se determina como el cociente del vector y su longitud, \[\vec e = \frac{\vec u}{|\vec u|} = \left(\frac{20}{20\sqrt{2}}, \frac{-20}{20\sqrt{2}}\right) = \left(\frac{1}{\sqrt{2}}, \frac{-1}{\sqrt{2}}\right).\]
Las ecuaciones paramétricas resultantes de la línea \(p\) son por lo tanto \[ \begin{align*} x &= -20 + t \cdot \frac{1}{\sqrt{2}}, \\ y &= 20 - t \cdot \frac{1}{\sqrt{2}}, \qquad t\in\mathbb R. \end{align*} \]
Tarea 2. Modificar el procedimiento de la Tarea 1 para que el sondeo quede perpendicular al segmento definido por los sensores del tomógrafo acústico.
Solución. Es necesario reemplazar el vector \(\vec u\) por un vector de dirección perpendicular a la línea definida por los sensores del tomógrafo acústico. Los vectores de dirección perpendiculares al vector \(\vec v = (v_1,v_2)\) jsou \((-v_2,v_1)\) a \((v_2,-v_1)\). El vector del punto \(P_2\) al punto \(P_3\) tiene coordenadas \[\vec v = P_3 - P_2 = (-25, 14) - (-15, 26) = (-10,-12).\] En nuestro caso, para la perpendicular a este vector tenemos las opciones: \[ \vec n_{1} = (12, -10), \quad \vec n_{2} = (-12, 10). \] De la Figura 2 se puede observar que el vector de dirección debe apuntar hacia la derecha y hacia abajo, por lo que usaremos el vector \(\vec n_{1}\). La longitud del vector \(\vec n_{1}\) viene dada por la relación \[|\vec n_{1}| = \sqrt{12^2 + (-10)^2} = \sqrt{244} = 2\sqrt{61}\] y el vector unitario en la dirección del vector \(\vec n_{1}\) es el cociente del vector por su longitud, es decir: \[\vec e = \frac{\vec n_{1}}{|\vec n_{1}|} = \left(\frac{12}{2\sqrt{61}}, \frac{-10}{2\sqrt{61}}\right) = \left(\frac{6}{\sqrt{61}}, \frac{-5}{\sqrt{61}}\right).\]
La ecuación paramétrica de la recta \(p\) es por tanto \[ \begin{align*} x &= -20 + t \cdot \frac{6}{\sqrt{61}}, \\ y &= 20 - t \cdot \frac{5}{\sqrt{61}}, \qquad t\in\mathbb R. \end{align*} \]
Nota. El procedimiento descrito en las tareas anteriores puede utilizarse con dos sensores tomógrafos acústicos cualesquiera y puede algoritmizarse fácilmente. El resultado será una combinación de datos del resistógrafo y del tomógrafo acústico en una sola imagen.
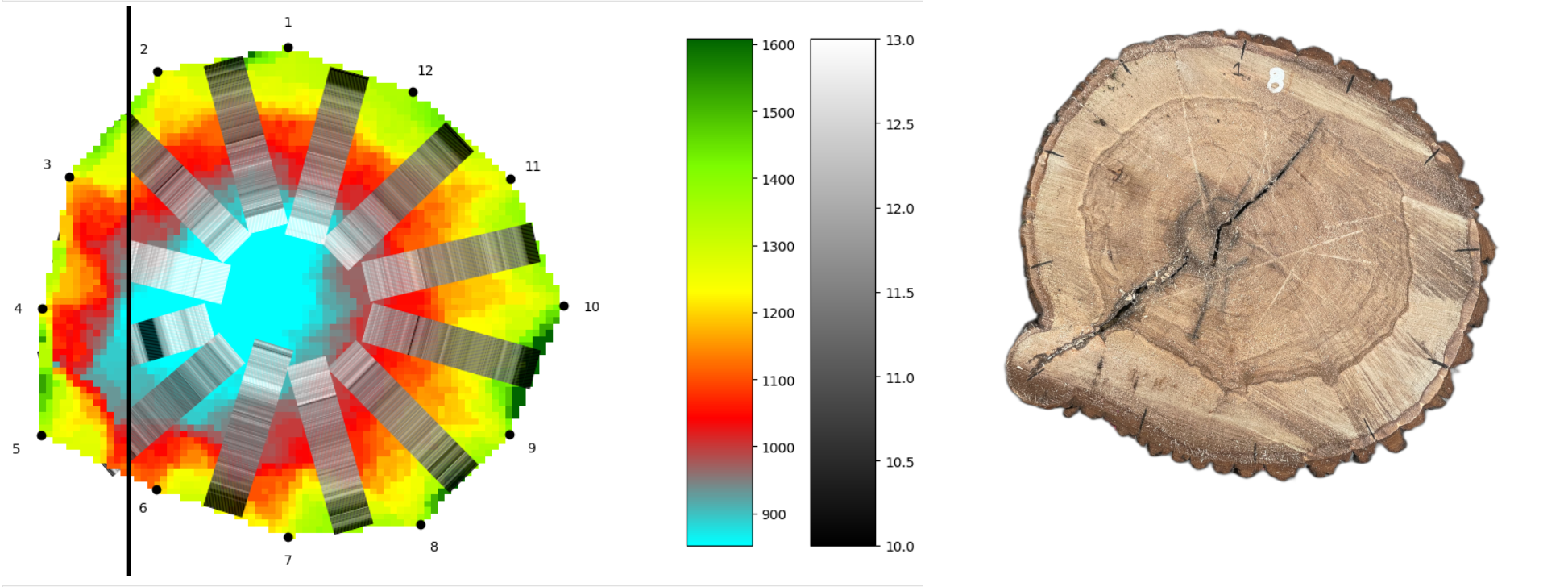
Fuente de datos
Los datos y fotografías de este texto provienen de mediciones reales realizadas en en árboles de la hilera de tilos de Wallenstein, en Jičín. Esta es la hilera de tilos más antigua de la República Checa y tiene una longitud de más de 1700 metros. Dado que no todos los árboles gozan de buena salud, es necesario revisar su estado periódicamente. Como parte del monitoreo, se seleccionaron algunos árboles para la tala y se tomaron mediciones en ellos antes de la misma. Esto brindó una oportunidad única para comparar los resultados de las mediciones con el estado real. Estas mediciones fueron realizadas por el arborista Vojtěch Semík y los datos se procesaron en el marco del proyecto ERC CZ DYNATREE (https://starfos.tacr.cz/cs/projekty/LL1909).
Conclusión
En este texto, nos familiarizamos con las posibilidades de aplicar el aparato de geometría analítica al combinar datos de un tomógrafo acústico y un resistógrafo. Hemos mostrado cómo usar la ecuación paramétrica de una línea recta para convertir la profundidad del pozo de un resistógrafo a coordenadas en el sistema de coordenadas del tomograma. Este procedimiento permite mejorar la predicción de la salud de los árboles y obtener una visión completa de su estado.
La combinación de datos de ambos métodos permite obtener información más precisa sobre el estado de la madera y detectar posibles defectos ocultos, lo cual es importante para la salud y la seguridad de los árboles en zonas urbanas.
Bibliografía y fuente de las imágenes
Bibliografía
- https://rinntech.info/products/resistograph/ (online, přístup 6.6.2025)
- https://www.kudyznudy.cz/aktivity/valdstejnska-lipova-alej-v-jicine-nejstarsi-doch (online, přístup 6.6.2025)
- https://www.jicin.org/lipova-alej (online, přístup 6.6.2025)
- https://zpravyceskyraj.cz/stromy-vedi-co-a-proc-delaji-arborista-vojtech-semik-o-jicinske-lipove-aleji/ (online, přístup 6.6.2025)
Fuente de las imágenes
- Projekt DYNATREE – Tree Dynamics: Understanding of Mechanical Response to Loading, https://starfos.tacr.cz/cs/projekty/LL1909.
- Vlastní obrázky