Instructions for translators

1. Open this file on GitHub server. If you see https://um.mendelu.cz/... in URL, click View on GitHub to open this file on github.com.
2. If you see this file on GitHub server, you can edit the content of the file. Open the file in an editor. You can use simple editor (pres e on GitHub). However, an advanced VS Code editor (press . on GitHub) is better, since it provides preview how the Markdown code renders. Alternatively press pencil for simple editor or press triangle next to the pencil to get access to VS Code described as github.dev.
3. Fix the keywords in the preamble.
4. Depending on which language version you want to use as a source for your translation, delete either English or Czech version below.
5. Translate to your language. Keep Markdown marking and math notation. If you use a tool to get first version of the translation, make sure that the markup is preserved.
6. In VS Code you can open the preview in another window by pressing Ctrl+V and K. Keep the preview open as you work, or close using a mouse.
7. Instead of saving, you have to commit and push the changes to the repository. Fill the Message under Source control (describe your changes, such as “Polish translation started”) and then press Commit&Push.
8. Make sure that your changes appear in the commit history. In rare cases (if you work with simultaneously with someone else) you have to download /Pull/ and merge his and yours changes. Usualy Sync (Pull & Push) should work.
9. When you finish the translation, change is_finished: False in header to is_finished: True.

Instrukce pro překladatele

1. Otevřete tento soubor na serveru GitHub. Pokud máte soubor otevřen na https://um.mendelu.cz/..., otevřete jej na serveru github.com.
2. Pokud tento soubor vidíte na serveru GitHub, můžete obsah souboru upravit. Otevřete soubor v editoru. Můžete použít jednoduchý editor (stiskněte e na GitHubu). Lepší je však pokročilý editor VS Code (stikněte . na GitHubu), protože poskytuje náhled, jak se kód Markdown interpretuje. Případně stiskněte tužku pro jednoduchý editor nebo stiskněte trojúhelníček vedle tužky, abyste získali přístup k editoru VS Code popsaný jako github.dev.
3. Opravte klíčová slova v preambuli.
4. V závislosti na tom, kterou jazykovou verzi chcete použít jako zdrojový kód pro svůj překladu, odstraňte níže uvedenou anglickou nebo českou verzi.
5. Přeložte do svého jazyka. Ponechte značení Markdown a matematický zápis. Pokud použijete nástroj typu DeepL pro získání první verze překladu, ujistěte se, že zápis matematických výrazů byl zachován.
6. Ve VS Code můžete náhled otevřít v jiném okně stisknutím Ctrl+V. a K. Během práce nechte náhled otevřený nebo jej zavřete pomocí myši.
7. Místo uložení musíte změny zaregistrovat a odeslat do úložiště. Vyplňte zprávu v poli Zpráva (popište své změny, např. “Zahájen překlad do polštiny”) a poté stiskněte tlačítko Commit&Push.
8. Ujistěte se, že se vaše změny objeví v historii revizí. Ve výjimečných případech (pokud pracujete současně s někým jiným) musíte stáhnout /Pull/ a sloučit jeho a vaše změny. Obvykle by synchronizace (Pull & Push) měla fungovat.
9. Po dokončení překladu změňte is_finished: False v záhlaví na is_finished: True.

Czech source

Akustický tomograf a rovnice elipsy

15 min., 1/3

Představte si, že potřebujete posoudit zdravotní stav starého stromu, aniž byste ho museli porazit nebo do něj řezat. Moderní technologie dnes umožňují takové posouzení provést šetrně a přitom přesně – a jedním z klíčových nástrojů je přitom rovnice elipsy. Pomocí metody EBSI (elliptise-based spatial interpolation) lze z naměřených dat odhadnout fyzikální vlastnosti dřeva uvnitř kmene a získat tak představu o jeho pevnosti a zdraví. K tomu je ale třeba umět zacházet s rovnicí elipsy i tehdy, když je elipsa v obecné poloze vzhledem k osám. V takovém případě využijeme skalární součin pro nalezení projekce vektoru do požadovaného směru.

Akustický tomograf

V praxi arboristy, odborníka pro péči o dřeviny mimo les, je častým úkolem posouzení vitality a zdravotního stavu stromu. Toto je nutné udělat s nulovým nebo minimálním zásahem, který kondici stromu výrazně neovlivní. Jednou z velmi málo invazivních metod je použití akustického tomografu. Jedná se o přístroj, který dokáže měřit “dobu letu” zvukového signálu (anglicky používaný termín time of flight, TOF) mezi dvěma senzory. S pomocí metod analytické geometrie je poté možno určit vzdálenost mezi senzory a s využitím předpokladu o šíření zvukových signálů přímými paprsky se dá zjistit rychlost šíření zvuku v materiálu. Tato hodnota je velice důležitým indikátorem fyzikálně-mechanických vlastností, protože ve zdravém dřevě (angl. sound wood) se zvuk šíří rychleji než ve dřevě degradovaném (angl. degraded wood).

Problematika rekonstrukce obrazu

Rekonstrukce obrazu v akustickém tomografu vychází z předpokladu přímého šíření paprsků v řezu kmene. Nejsou tedy brány v úvahu odrazy nebo lom vlnění. Kvalita tohoto předpokladu je předmětem aktuálního vědeckého zkoumání, nicméně předpoklad tohoto typu je nutné pro praktické využití metody učinit.

Protože se vychází z poměrně malého množství paprsků (akustický tomograf má typicky 12, nejvýše 24 senzorů, pro stromy malého průměru i méně), je nutné využít nějakou metodu interpolace a průměrování. Tímto se úloha stává odlišnou například od tomografů používaných ve zdravotnictví, kde zobrazovacích paprsků je řádově více a je také lépe definována geometrie měření: zdroje a snímače jsou umístěny například po obvodu kruhu a nikoliv po nepravidelném obvodu kmene stromu. Pro odstranění nedostatků spojených s použitím akustického tomografu pro stromy bylo vyvinuto několik technik, které umožňují interpolaci a průměrování naměřených hodnot.

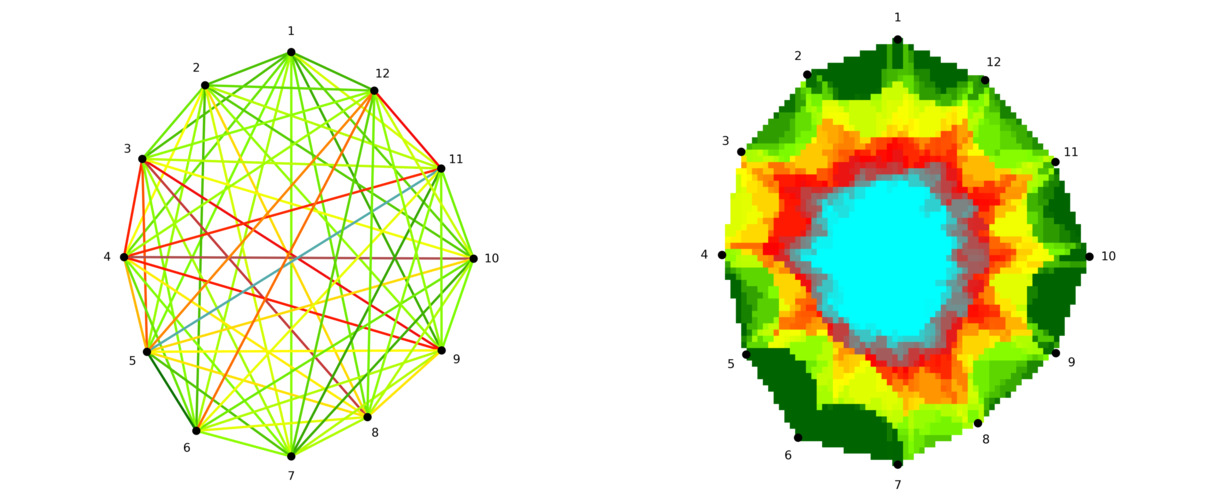
EBSI metoda a její následovníci

Řada metod rekonstrukce obrazu v akustickém tomografu vychází z předpokladu, že rychlost šíření zvuku je ovlivněna kvalitou dřeva v eliptickém okolí spojnice dvou senzorů. Tento předpoklad byl otestován na reálných měřeních v Du et al. (2015), kde byl navržen i vzorec, dávající do souvislosti vzdálenost senzorů a excentricitu elipsy. Tento přístup zaznamenal lepší výsledky než postupy založené na prostém průsečíku paprsků a průměrování rychlostí v těchto průsečících. Metoda dostala název Ellipse-based spatial interpolation a zkratku EBSI.

Praktická implementace metody rekonstrukce obrazu spočívá v tom, že průřez kmene se rozdělí na jednotlivé buňky, ve kterých se naměřené hodnoty v jistém smyslu zprůměrují. V EBSI metodě pro každou buňku určíme rychlost jako průměr rychlostí všech paprsků, v jejichž eliptickém okolí působnosti se buňka nachází.

V dalších pracích byla metoda EBSI ještě rozšířena Okolo každého paprsku uvažujeme opět elipsu definující oblast působnosti tohoto paprsku (viz. Obrázek 3). Data se zpracovávají dvoukolově metodami RSEN a SISE (z anglického ray sementation by elliptical neighborhood a spatial interpolation by segmented ellipse) popsanými v Du et al (2018).

Detailní popis metod je možné najít v původní literatuře, nicméně i z uvedeného zjednodušeného popisu je zřejmé, že zásadní dílčí úlohou při implementaci obrazové rekonstrukce je ověření, zda bod v rovině leží uvnitř elipsy či zda leží vně.

Rovnice elipsy

Z předešlé motivační části vyplývá, že pro praktickou implementaci rekonstrukce obrazu pomocí EBSI metody je nutné umět efektivně pracovat s elipsou v různých polohách, což zahrnuje libovolné pootočení os a libovolné posunutí středu elipsy. Potřebujeme efektivně zjišťovat, zda nějaký bod leží uvnitř či vně elipsy.

Elipsa je množina bodů v rovině, pro které platí, že součet vzdáleností bodu od dvou ohnisek je konstantní. Elipsu je možno určit pomocí hlavní a vedlejší osy. Uvažujme elipsu s délkou hlavní poloosy \(a\) a délkou vedlejší poloosy \(b\). Rovnice elipsy se středem v počátku soustavy souřadnic a hlavní osou ve směru osy \(x\) má v tomto případě tvar \[ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1. \] Body ležící uvnitř elipsy pak splňují nerovnici \[ \frac{x^2}{a^2}+\frac{y^2}{b^2}<1. \] My však pracujeme s elipsami v obecné poloze, jejich rovnice se sice dají transformovat do stejného tvaru, ale to je poněkud pracný a pro naše účely i zbytečný proces. Raději než pracovat se souřadnicemi budeme využívat vzdáleností bodu od hlavní a od vedlejší poloosy. Pokud má elipsa výše uvedenou rovnici, tak tyto vzdálenosti jsou přímo \(x\)-ové a \(y\)-ové souřadnice daného bodu.

Tedy je-li \(d_1\) vzdálenost bodu od přímky definované vedlejší osou (pro stručnost vzdálenost od vedlejší osy) a vzdálenost bodu od hlavní osy \(d_2\), pak bod leží uvnitř elipsy právě tehdy, když platí \[ \frac{d_1^2}{a^2}+\frac{d_2^2}{b^2}<1.\tag{1} \] Pro ověření zda bod leží nebo neleží uvnitř elipsy tedy stačí určit vzdálenost bodu od hlavní a od vedlejší osy a ověřit platnost výše uvedené nerovnosti (1).

Délka projekce vektoru a skalární součin

Obrázek znázorňuje hlavní a vedlejší osy elipsy, jednotkové vektory ve směru těchto os, spojnici testovaného bodu se středem elipsy a vyznačení vzdáleností bodu od jednotlivých os elipsy.

Pro jednoduchost uvažujme, že úhel mezi vektory \(\vec u\) a \(\vec e_1\) je ostrý. Z definice skalárního součinu a z faktu, že vektor \(\vec e_1\) je jednotkovým vektorem plyne

\[\vec u\cdot\vec e_1 = |\vec u||\vec e_1|\cos\varphi = |\vec u| \cos\varphi = d_1.\]

Vzdálenost od vedlejší osy je tedy možno určit pomocí skalárního součinu. Kolmý průmět vektoru do přímky se nazývá projekce a z obrázku je patrné, že \(d_1\) je vlastně délka projekce vektoru \(\vec u\) do směru určeného vektorem \(\vec e_1\). V případě, že by úhel mezi vektory \(\vec u\) a \(\vec e_1\) byl tupý, vychází hodnota \(d_1\) záporná, což se však v testovacím kriteriu (1) neprojeví.

Analogicky, délka projekce vektoru \(\vec u\) do směru definovaného vektorem \(\vec e_2\) je (až na případné znaménko, které se opět v testu (1) neprojeví) dána vztahem

\[d_2=\vec u\cdot \vec e_2.\]

Poznámka. Poznamenejme, že výpočet skalárního součinu se provádí pomocí souřadnic podle vzorce

\[\vec u\cdot\vec v = u_1v_1+u_2v_2,\]

kde \(\vec u = (u_1, u_2)\) a \(\vec v=(v_1,v_2)\). Tento výpočet je možné realizovat v počítačích velmi rychle a použitím vhodných programovacích technik (vektorizace) je možné výpočet provést současně pro tisíce bodů řádově stokrát rychleji než použitím cyklu založeného na postupném testování jednotlivých bodů.

Poznámka. Jednotkový vektor \(\vec e_1\) ve směru hlavní osy je možné určit buď jako podíl vektoru ze středu do hlavního vrcholu a délky tohoto vektoru, anebo pomocí úhlu, který svírá hlavní osa s osou \(x\). Je-li tento úhel \(\alpha\), je jednotkový vektor dán vztahem

\[\vec e_1=(\cos\alpha, \sin\alpha).\]

Jednotkový vektor ve směru vedlejší osy je na \(\vec e_1\) kolmý. Je tedy možné brát například

\[\vec e_2 = (-\sin\alpha, \cos\alpha).\]

Ukázka použití

Řešení. Jednotkový vektor se směru hlavní osy je \(\vec e_1=(\cos 30^\circ, \sin 30^\circ)\). Vektor \(\vec u\) je dán souřadnicemi bodu \(X\), tj. \(\vec u=(1{,}6;1{,}6)\). Skalární součin je tedy

\[d_1=\vec u\cdot \vec e_1 = 1{,}6\cdot\cos 30^\circ + 1{,}6\cdot\sin 30^\circ\doteq 2{,}186.\]

Podobně, délka projekce do směru vedlejší osy dané vektorem \(\vec e_2=(-\sin 30^\circ,\, \cos 30^\circ)\) je

\[d_2=\vec u\cdot \vec e_2 = -1{,}6\cdot\sin 30^\circ + 1{,}6\cdot\cos 30^\circ \doteq 0{,}586.\]

Platí

\[ \frac{d_1^2}{a^2} + \frac{d_2^2}{b^2} \doteq 0{,}683<1. \]

Bod tedy leží uvnitř elipsy. Situace je na následujícím obrázku.

Závěr

V textu byly představeny základní kroky, na nichž je založena rekonstrukce obrazu v akustickém tomografu. Jedním z dílčích úkolů je ověření, zda zkoumaný bod leží uvnitř či vně elipsy, která je v obecné poloze a je zadána svými poloosami. Pro toto ověření je výhodné použít rovnici elipsy založenou nikoliv na souřadnicích, ale na vzdálenostech od hlavní a vedlejší osy. Tuto vzdálenost je možné určit pomocí skalárního součinu vektorů.

Literatura a zdroje obrázků

Literatura

1. Du, X., Li, S., Li, G., Feng, H., and Chen, S. (2015). “Stress wave tomography of wood internal defects using ellipse-based spatial interpolation and velocity compensation,” BioRes. 10(3), 3948-3962. http://doi.org/10.15376/biores.10.3.3948-3962
2. Du, X.; Li, J.; Feng, H.; Chen, S. Image Reconstruction of Internal Defects in Wood Based on Segmented Propagation Rays of Stress Waves. Appl. Sci. 2018, 8, 1778. https://doi.org/10.3390/app8101778

Zdroje obrázků

1. Projekt DYNATREE – Tree Dynamics: Understanding of Mechanical Response to Loading, https://starfos.tacr.cz/cs/projekty/LL1909.
2. Vlastní obrázky

English source

Not available on July 10. If you want to start from English translation, wait until it appears on https://um.mendelu.cz/math4u/site/ anc copy the English text by hand.