V praxi se často setkáváme s tím, že hodnotami jedné veličiny jsou dány hodnoty druhé veličiny a ze sady naměřených nebo statisticky získaných dat určujeme matematický model udávající funkční závislost mezi oběma veličinami. Jako příklad můžeme uvažovat data udávající výšku a hmotnost amerických žen ve věku mezi 30 a 39 lety (zdroj https://en.wikipedia.org/wiki/Simple_linear_regression, 12.4.2024, pro stručnost je použita jenom polovina dat).
| výška/m | \(1{,}47\) | \(1{,}52\) | \(1{,}57\) | \(1{,}63\) | \(1{,}68\) | \(1{,}73\) | \(1{,}78\) | \(1{,}83\) |
|---|---|---|---|---|---|---|---|---|
| hmotnost/kg | \(52{,}21\) | \(54{,}48\) | \(57{,}20\) | \(59{,}93\) | \(63{,}11\) | \(66{,}28\) | \(69{,}92\) | \(74{,}46\) |
Data jsou vykreslena na obrázku vlevo. Z obrázku je patrné, že s rostoucí výškou roste i hmotnost. V takovém případě je možné najít matematický model, který udává hmotnost jako funkci výšky. Takový matematický model je znázorněn barevně na obrázku vpravo. Jedná se o model, který umožní pro zadanou výšku ženy předpovědět její hmotnost.
Popsaná úloha se nazývá lineární regrese.
Lineární regrese je jednou ze základních metod strojového učení, kdy v datech odhalíme jistou funkční závislost. Tuto poté můžeme použít k tomu, abychom dávali predikce funkčních hodnot pro data, která se v zadaném souboru nevyskytují.
V následujícím si ukážeme, jak lineární regrese souvisí s lineární kombinací vektorů, a jak je možné regresní přímku najít pomocí operací s vektory. Budeme postupovat po malých krocích:
Úloha 1. Zapište vektor \(\vec c = \begin{pmatrix}1 \cr 2\end{pmatrix}\) jako lineární kombinaci vektorů \(\vec a = \begin{pmatrix}2 \cr 2\end{pmatrix}\) a \(\vec b = \begin{pmatrix}3 \cr 1\end{pmatrix}\).
Řešení. Zapsat vektor \(\vec c\) jako kombinaci vektorů \(\vec a\) a \(\vec b\) znamená najít čísla \(t_1\) a \(t_2\) taková, že \[ t_1 \vec a + t_2 \vec b = \vec c. \] Po rozepsání do souřadnic vidíme, že tato úloha vede na soustavu rovnic \[ \begin{aligned} 2t_1+3t_2 &= 1,\cr 2t_1+t_2 &=2. \end{aligned} \] Tato soustava má jediné řešení \(t_1=\frac 54\) a \(t_2=-\frac 12\).
Úloha 2. Napište vektor \(\vec w=\begin{pmatrix}1\cr 2\cr 1\end{pmatrix}\) jako lineární kombinaci vektorů \[ \vec u_1=\begin{pmatrix}2\cr 2\cr 1\end{pmatrix},\quad \vec u_2=\begin{pmatrix}3\cr 1\cr 2\end{pmatrix},\quad \vec u_3=\begin{pmatrix}3\cr -1\cr -4\end{pmatrix}. \]
Řešení. Podobně jako v předchozí úloze hledáme čísla \(t_1\), \(t_2\) a \(t_3\) taková, že \[ t_1 \vec u_1+t_2\vec u_2 + t_3 \vec u_3 = \vec w.\tag{1} \] Po dosazení a rozepsání do souřadnic dostáváme soustavu tří rovnic o třech neznámých \[\tag{2} \begin{aligned} 2t_1 + 3t_2 + 3t_3 &= 1,\cr 2 t_1 + t_2 -t_3 &=2,\cr t_1+2t_2-4t_3&=1. \end{aligned} \] Řešení takové soustavy je již poměrně nepříjemné. Pomocí sčítací nebo dosazovací metody bychom mohli ale zjistit, že \[ t_1=\frac{14}{13},\quad t_2=-\frac{7}{26},\quad t_3=-\frac{3}{26}. \]
Pokud je alespoň jeden ze zadaných vektorů kolmý ke zbylým vektorům, můžeme šikovným trikem získat jednodušší soustavu rovnic.
Vraťme se k předchozí úloze. Můžeme si všimnout, že vektor \(\vec u_3\) je kolmý k vektorům \(\vec u_1\) a \(\vec u_2\). Tím pádem je i kolmý k rovině definované těmito vektory. Tuto skutečnost snadno ukážeme výpočtem skalárních součinů \[ \vec u_1\cdot \vec u_3 = 2\cdot 3 +2\cdot (-1)+1\cdot (-4) = 0 \] a \[ \vec u_2\cdot \vec u_3 = 3\cdot 3 +1\cdot (-1)+2\cdot (-4) = 0. \] Díky této vlastnosti se vyplatí rovnici (1) vynásobit skalárně po řadě vektory \(\vec u_1\) až \(\vec u_3\). Tím dostáváme následující tři rovnice. \[ \begin{aligned} t_1 (\vec u_1\cdot \vec u_1) + t_2 (\vec u_2\cdot \vec u_1) + t_3 (\vec u_3\cdot \vec u_1) &= \vec w\cdot \vec u_1\cr t_1 (\vec u_1\cdot \vec u_2) + t_2 (\vec u_2\cdot \vec u_2) + t_3 (\vec u_3\cdot \vec u_2) &= \vec w\cdot \vec u_2\cr t_1 (\vec u_1\cdot \vec u_3) + t_2 (\vec u_2\cdot \vec u_3) + t_3 (\vec u_3\cdot \vec u_3) &= \vec w\cdot \vec u_3 \end{aligned} \] Výpočtem skalárních součinů dostáváme soustavu, která je nepoměrně jednodušší než soustava (2). \[ \begin{aligned} 9t_1+10t_2=7\cr 10t_1+14t_2=7\cr 26t_3=-3 \end{aligned} \] Z poslední rovnice vidíme přímo jednu z neznámých a dvě první rovnice tvoří soustavu dvou rovnic o dvou neznámých \(t_1\) a \(t_2\).
Připomeňme, že za nekonzistentní označujeme takové soustavy lineárních rovnic, které nemají řešení.
Naši úlohu o nalezení vyjádření vektoru jako lineární kombinace daných vektorů modifikujeme. Jeden z vektorů, se kterými pracujeme, vynecháme. Tím se stane úloha v klasickém smyslu neřešitelnou.
Úloha 3. Napište vektor \(\vec w=\begin{pmatrix}1\cr 2\cr 1\end{pmatrix}\) jako lineární kombinaci vektorů \[ \vec u_1=\begin{pmatrix}2\cr 2\cr 1\end{pmatrix},\quad \vec u_2=\begin{pmatrix}3\cr 1\cr 2\end{pmatrix}. \]
Řešení. Musíme najít čísla \(t_1\), \(t_2\) taková, že platí \[t_1\vec u_1 + t_2\vec u_2 = \vec w.\] Rozepsáním v souřadnicích dostaneme soustavu \[ \begin{aligned} 2t_1 + 3t_2 &= 1,\cr 2 t_1 + t_2 &=2,\cr t_1+2t_2&=1. \end{aligned} \] Je snadné se přesvědčit, že tato soustava je nekonzistentní a nemá řešení. Opravdu, soustavu složenou z prvních dvou rovnic jsme vyřešili v úvodu (\(t_1=\frac 54\) a \(t_2=-\frac 12\)) a poslední rovnice je s touto volbou ve sporu (\(\frac 54+2\cdot(-\frac 12)\neq 1\)).
Pojďme nyní rozumným způsobem zobecnit pojem řešení. Nebudeme hledat hodnoty neznámých, pro které jsou si levé a pravé strany rovny. Namísto toho budeme hledat alespoň takové hodnoty neznámých, pro které se levé a pravé strany co nejméně liší.
Řešením nekonzistentní soustavy rovnic budeme rozumět takovou volbu hodnot neznámých, pro kterou je délka vektoru vyjadřujícího rozdíl levých a pravých stran soustavy minimální.
Na obrázku si vysvětlíme, co daná soustava vyjadřuje a jak je možné si představit její řešení ve výše uvedeném oslabeném smyslu.
Snažíme se pomocí lineární kombinace vektorů \(\vec u_1\) a \(\vec u_2\) vyjádřit vektor \(\vec w\), který ale neleží v rovině definované těmito vektory. Taková úloha nemá řešení. Budeme se proto snažit najít alespoň takovou lineární kombinaci, která se od vektoru \(\vec w\) liší co nejméně.
Tato kombinace je dána vektorem \(\vec w_0\), přičemž rozdíl mezi \(\vec w\) a \(\vec w_0\) je znázorněn vektorem \(\vec \varepsilon\). Snažíme se o to, aby délka vektoru \(\vec \varepsilon\) byla co nejmenší.
Z názorného pohledu a geometrických vlastností je snadné nahlédnout, že toto nastane v případě, kdy je vektor \(\vec \varepsilon\) kolmý k rovině určené vektory \(\vec u_1\) a \(\vec u_2\). Tím se dostáváme do stejné situace, jako při alternativním řešení třetí úlohy. Tam jsme také viděli trik, jak najít koeficienty u vektorů \(\vec u_1\) a \(\vec u_2\) bez řešení plné soustavy rovnic: vynásobili jsme soustavu skalárně vektory \(\vec u_1\) a \(\vec u_2\). Dokonce k tomuto výpočtu ani nemusíme znát vektor \(\vec \varepsilon\).
Protože délka vektoru \(\vec\varepsilon\) se vyjadřuje pomocí druhých mocnin souřadnic tohoto vektoru, má metoda název metoda nejmenších čtverců.
Celý postup si ukážeme na následujícím příkladě.
Uvažujme data z následující tabulky.
| \(x\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|
| \(y\) | \(1\) | \(5\) | \(7\) |
Hledáme přímku \(y=ax+b\), která co nejlépe vystihuje trend v tomto souboru a byla by vhodným matematickým modelem pro tato data. Dosazením každého ze tří bodů do rovnice přímky dostáváme soustavu tří rovnic o dvou neznámých. \[ \begin{aligned} 2a+b=1\cr 3a+b=5\cr 4a+b=7 \end{aligned} \] To je úloha s nekonzistentní soustavou rovnic (tzv. přeurčenou soustavou), která nemá řešení v klasickém slova smyslu. Vektorový tvar této soustavy je následující. \[ a \begin{pmatrix}2\\3\\4\end{pmatrix} + b \begin{pmatrix}1\\1\\1\end{pmatrix} = \begin{pmatrix}1\\5\\7\end{pmatrix} \] Po vynásobení po řadě vektory \(\begin{pmatrix}2\\3\\4\end{pmatrix}\) a \(\begin{pmatrix}1\\1\\1\end{pmatrix}\) dostáváme soustavu dvou rovnic. \[ \begin{aligned} 29a+9b&=45\\ 9a+3b&=13 \end{aligned} \] Řešení této soustavy je \(a=3\) a \(b=-\frac {14}3\). Regresním modelem pro zadaná data je tedy přímka \[y=3x-\frac {14}3.\] Graf obsahující uvedená data a regresní přímku je na obrázku.
Postup uvedený v předchozím textu pro tři body je možné zobecnit na libovolný počet bodů. Není neobvyklé pracovat s datovým souborem obsahujícím stovky bodů.
Je-li vektor \(\vec X\) vektorem obsahujícím hodnoty nezávislé proměnné1 a \(\vec Y\) vektor obsahující hodnoty závislé proměnné, budeme uvažovat model2 \[ \vec Y = a\vec X+b. \] Koeficienty \(a\) a \(b\) určíme tak, že tuto rovnici přepíšeme na vektorovou rovnici \[ \vec Y = a\vec X+b\vec 1, \] kde \(\vec 1\) je vektor sestavený z jedniček. Tuto rovnici vynásobíme skalárně vektorem \(\vec X\) a vektorem \(\vec 1\). Dostáváme tak soustavu \[ \begin{aligned} a(\vec X\cdot \vec X)+ b(\vec X\cdot \vec 1) &= \vec X\cdot \vec Y \cr a(\vec 1\cdot \vec X)+ b(\vec 1\cdot \vec 1) &= \vec 1\cdot \vec Y \cr \end{aligned}\tag{3} \]
Pro více než tři body takto pracujeme s vektory větší dimenze než tři. V důsledku toho přicházíme o názornou geometrickou představu. Až na tuto skutečnost se však na práci nic nemění. Skalární součin dvou vektorů se stále počítá tak, že se vynásobí odpovídající komponenty a tyto součiny se poté sečtou.
Úloha 4. Nalezněte vhodný lineární model pro tabulku dat z úvodního textu.
Řešení. Připomeňme si uvedená data:
| výška/m | \(1{,}47\) | \(1{,}52\) | \(1{,}57\) | \(1{,}63\) | \(1{,}68\) | \(1{,}73\) | \(1{,}78\) | \(1{,}83\) |
|---|---|---|---|---|---|---|---|---|
| hmotnost/kg | \(52{,}21\) | \(54{,}48\) | \(57{,}20\) | \(59{,}93\) | \(63{,}11\) | \(66{,}28\) | \(69{,}92\) | \(74{,}46\) |
Po dosazení dat do potřebných skalárních součinů dostaneme:
\[ \begin{aligned} \vec X\cdot\vec X&= 1{,}47^2 + 1{,}52^2+1{,}57^2+\cdots+1{,}83^2=21{,}9257\cr \vec X\cdot\vec Y&= 1{,}47 \cdot 52{,}21 + 1{,}52\cdot 54{,}48 + 1{,}57\cdot 57{,}20+\cdots+ 1{,}83\cdot 74{,}46=828{,}4568\cr \vec 1\cdot\vec X&= 1{,}47 + 1{,}52+ 1{,}57+\cdots+ 1{,}83= 13{,}21\cr \vec 1\cdot\vec Y&= 52{,}21 + 54{,}48+57{,}20+\cdots+74{,}46=497{,}59\cr \vec 1\cdot\vec 1 &= 1+1+1+\cdots +1=8 \end{aligned} \]
Po dosazení hodnot do (3) dostáváme soustavu dvou rovnic o dvou neznámých
\[ \begin{aligned} 21{,}9257a+13{,}21b&=828{,}4568,\cr 13{,}21a+8b&=497{,}59, \end{aligned} \]
která má jediné řešení. Tímto řešením3 je \(a=60{,}44\) a \(b=-37{,}61\). Modelem, který udává závislost hmotnosti žen \(y\) na jejich výšce \(x\), je vztah \[y=60{,}44x-37{,}61.\]
Obrázek 4 ukazuje použitá data, regresní závislost a predikci pro hmotnost ženy o výšce \(1{,}72\) metru.
Úloha 5. Najděte regresní přímku pro zadaná data.
| \(x\) | \(1{,}0\) | \(2{,}0\) | \(3{,}0\) | \(4{,}0\) |
|---|---|---|---|---|
| \(y\) | \(2{,}3\) | \(2{,}5\) | \(3{,}1\) | \(3{,}3\) |
Řešení.
Pro vektory \(\vec X\) a \(\vec Y\) dané po řadě první a druhou řadou tabulky dostáváme \[ \begin{aligned} \vec X\cdot\vec X&=1{,}0^2+2{,}0^2+3{,}0^2+4{,}0^2=30,\cr \vec X\cdot\vec Y&=1{,}0\cdot 2{,}3+2{,}0\cdot 2{,}5+3{,}0\cdot 3{,}1+4{,}0\cdot 3{,}3=29{,}8,\cr \vec 1\cdot\vec X&=1{,}0+2{,}0+3{,}0+4{,}0=10,\cr \vec 1\cdot\vec Y&=2{,}3+2{,}5+3{,}1+3{,}3=11{,}2,\cr \vec 1\cdot\vec 1&=1+1+1+1=4. \end{aligned} \]
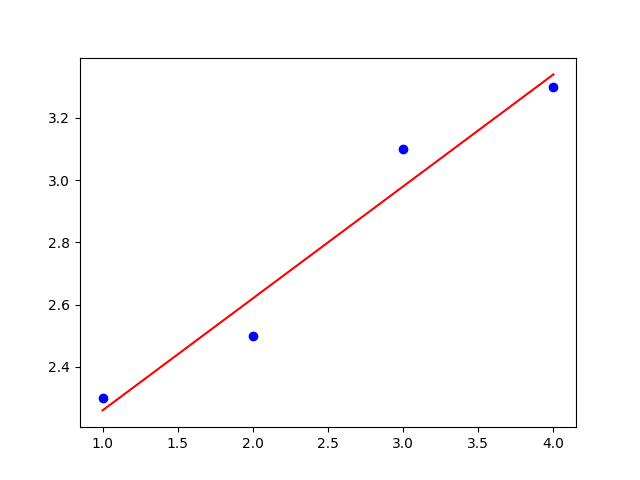
Soustava rovnic (3) po dosazení těchto hodnot má tvar \[ \begin{aligned} 30a+10b&=29{,}8,\cr 10a+4b&=11{,}2. \end{aligned} \] Řešením této soustavy je \(a=0{,}36\) a \(b=1{,}90\). Regresní přímka pro zadaná data je tedy \[y=0{,}36x+1{,}90.\] Obrázek ukazuje regresní přímku a zadaná data.
Použijeme zápis běžně užívaný při zpracování dat, kdy datové soubory (vektory) označujeme velkými písmeny a vektor, který má všechny komponenty rovny stejnému číslu zapisujeme jako dané číslo se šipkou pro označení vektoru.↩︎
Přísně vzato tato operace nemá matematicky smysl, protože sčítáme vektor s reálným číslem. Tuto operaci je nutno interpretovat po složkách, kdy toto sčítání znamená, že se reálné číslo změní na vektor příslušné dimenze tak, aby operace byla definována. Toto přizpůsobení se naýváme broadcasting. Ve výsledku ke každé komponentě vektoru \(a\vec X\) přičítáme hodnotu \(b\).↩︎
Pozor, úloha je poměrně citlivá na zaokrouhlování.↩︎