Regresja liniowa
 30 min.,
30 min.,  2/3
2/3 W praktyce często spotykamy się z sytuacjami, w których wartości jednej zmiennej determinują wartości drugiej. Na podstawie zestawu zmierzonych lub statystycznie uzyskanych danych próbujemy następnie znaleźć model matematyczny, który opisuje funkcjonalną zależność między dwiema zmiennymi. Na przykład rozważmy dane wskazujące wzrost i wagę amerykańskich kobiet w wieku od 30 do 39 lat (źródło: https://en.wikipedia.org/wiki/Simple_linear_regression, dostęp 12 kwietnia 2024 r.; dla zwięzłości wykorzystano tylko połowę danych).
| wzrost/m | \(1{,}47\) | \(1{,}52\) | \(1{,}57\) | \(1{,}63\) | \(1{,}68\) | \(1{,}73\) | \(1{,}78\) | \(1{,}83\) |
|---|---|---|---|---|---|---|---|---|
| waga/kg | \(52{,}21\) | \(54{,}48\) | \(57{,}20\) | \(59{,}93\) | \(63{,}11\) | \(66{,}28\) | \(69{,}92\) | \(74{,}46\) |
Dane zostały przedstawione na rysunku po lewej stronie. Z rysunku jasno wynika, że wraz ze wzrostem wzrostu rośnie również waga. W takim przypadku możliwe jest znalezienie modelu matematycznego, który wyraża wagę jako funkcję wzrostu. Taki model matematyczny przedstawiono w kolorze na rysunku po prawej stronie. Pozwala on przewidzieć wagę kobiety na podstawie jej wzrostu.
Opisany powyżej typ problemu nazywany jest regresją liniową.
Regresja liniowa jest jedną z podstawowych metod uczenia maszynowego. Polega ona na identyfikacji zależności funkcjonalnej ukrytej w zestawie danych. Po uzyskaniu tej relacji możemy użyć jej do przewidywania wartości funkcji dla danych wejściowych, które nie są zawarte w oryginalnym zbiorze danych.
W poniższej sekcji pokażemy, w jaki sposób regresja liniowa jest powiązana z kombinacjami liniowymi wektorów, i jak można znaleźć linię regresji za pomocą operacji na wektorach. Będziemy postępować krok po kroku:
- Najpierw sprawdzimy, jak wyrazić wektor jako liniową kombinację danych wektorów.
- Następnie zobaczymy, jak można uprościć to zadanie, jeśli jeden z wektorów jest prostopadły do pozostałych.
- Następnie zbadamy, jak znaleźć przybliżone rozwiązanie, gdy dokładne nie istnieje.
- Wreszcie, wykorzystamy te pomysły do rozwiązania problemu regresji liniowej - czyli skonstruujemy model matematyczny oparty na danych, który ujawni podstawowy trend i pozwoli nam przewidywać wartości nieobecne w zbiorze danych.
Kombinacja liniowa wektorów
Zadanie 1. Wyraź wektor \(\vec c = \begin{pmatrix}1 \cr 2\end{pmatrix}\) jako kombinację liniową wektorów \(\vec a = \begin{pmatrix}2 \cr 2\end{pmatrix}\) i \(\vec b = \begin{pmatrix}3 \cr 1\end{pmatrix}\).
Rozwiązanie. Wyrażenie wektora \(\vec c\) jako kombinacji wektorów \(\vec a\) i \(\vec b\) oznacza znalezienie liczb \(t_1\) i \(t_2\) takich, że \[ t_1 \vec a + t_2 \vec b = \vec c. \] Zapisanie tego we współrzędnych prowadzi do następującego układu równań: \[ \begin{aligned} 2t_1+3t_2 &= 1,\cr 2t_1+t_2 &=2. \end{aligned} \] Układ ten ma unikalne rozwiązanie: \(t_1=\frac 54\) i \(t_2=-\frac 12\).
Zadanie 2. Wyraź wektor \(\vec w=\begin{pmatrix}1\cr 2\cr 1\end{pmatrix}\) jako kombinację liniową wektorów \[ \vec u_1=\begin{pmatrix}2\cr 2\cr 1\end{pmatrix},\quad \vec u_2=\begin{pmatrix}3\cr 1\cr 2\end{pmatrix},\quad \vec u_3=\begin{pmatrix}3\cr -1\cr -4\end{pmatrix}. \]
Rozwiązanie. Podobnie jak w poprzednim zadaniu, szukamy liczb \(t_1\), \(t_2\) i \(t_3\) takich, że \[ t_1 \vec u_1+t_2\vec u_2 + t_3 \vec u_3 = \vec w.\tag{1} \] Podstawienie współrzędnych daje układ trzech równań z trzema niewiadomymi \[\tag{2} \begin{aligned} 2t_1 + 3t_2 + 3t_3 &= 1,\cr 2 t_1 + t_2 -t_3 &=2,\cr t_1+2t_2-4t_3&=1. \end{aligned} \] Rozwiązanie takiego układu jest już nieco żmudne, ale stosując metodę podstawiania lub eliminacji, znajdujemy: \[ t_1=\frac{14}{13},\quad t_2=-\frac{7}{26},\quad t_3=-\frac{3}{26}. \]
Kombinacja liniowa z wykorzystaniem iloczynu skalarny
Jeśli przynajmniej jeden z podanych wektorów jest prostopadły do pozostałych wektorów, możemy użyć sprytnej sztuczki, aby uzyskać prostszy układ równań.
Wróćmy do poprzedniego zadania. Możemy zauważyć, że wektor \(\vec u_3\) jest prostopadły do wektorów \(\vec u_1\) i \(\vec u_2\). Oznacza to, że jest on również prostopadły do płaszczyzny wyznaczonej przez te dwa wektory. Możemy to łatwo zweryfikować, obliczając iloczyn skalarny: \[ \vec u_1\cdot \vec u_3 = 2\cdot 3 +2\cdot (-1)+1\cdot (-4) = 0 \] i \[ \vec u_2\cdot \vec u_3 = 3\cdot 3 +1\cdot (-1)+2\cdot (-4) = 0. \] Dzięki tej właściwości warto pomnożyć równanie (1) za pomocą iloczynu kropkowego przez wektory od \(\vec u_1\) do \(\vec u_3\). W ten sposób otrzymujemy następujące trzy równania. \[ \begin{aligned} t_1 (\vec u_1\cdot \vec u_1) + t_2 (\vec u_2\cdot \vec u_1) + t_3 (\vec u_3\cdot \vec u_1) &= \vec w\cdot \vec u_1\cr t_1 (\vec u_1\cdot \vec u_2) + t_2 (\vec u_2\cdot \vec u_2) + t_3 (\vec u_3\cdot \vec u_2) &= \vec w\cdot \vec u_2\cr t_1 (\vec u_1\cdot \vec u_3) + t_2 (\vec u_2\cdot \vec u_3) + t_3 (\vec u_3\cdot \vec u_3) &= \vec w\cdot \vec u_3 \end{aligned} \] Obliczając iloczyny kropkowe, otrzymujemy układ, który jest znacznie prostszy niż układ (2). \[ \begin{aligned} 9t_1+10t_2=7\cr 10t_1+14t_2=7\cr 26t_3=-3 \end{aligned} \] Z ostatniego równania możemy bezpośrednio wyznaczyć jedną z niewiadomych, a pierwsze dwa równania tworzą układ dwóch równań z dwiema niewiadomymi, \(t_1\) i\(t_2\).
Kombinacje liniowe i niespójne układy równań
Przypomnijmy, że układ równań liniowych jest niespójny, jeśli nie ma rozwiązania.
Zmodyfikujemy teraz nasze poprzednie zadanie polegające na wyrażeniu wektora jako kombinacji liniowej podanych wektorów. Tym razem pominiemy jeden z wektorów, których używaliśmy poprzednio. W rezultacie problem stanie się nierozwiązywalny w klasycznym sensie.
Zadanie 3. Wyrazić wektor \(\vec w=\begin{pmatrix}1\cr 2\cr 1\end{pmatrix}\) jako kombinację liniową wektorów \[ \vec u_1=\begin{pmatrix}2\cr 2\cr 1\end{pmatrix},\quad \vec u_2=\begin{pmatrix}3\cr 1\cr 2\end{pmatrix}. \]
Rozwiązanie. Musimy znaleźć liczby \(t_1\), \(t_2\) takie, że \[t_1\vec u_1 + t_2\vec u_2 = \vec w.\] Zapisanie tego we współrzędnych prowadzi do następującego układu: \[ \begin{aligned} 2t_1 + 3t_2 &= 1,\cr 2 t_1 + t_2 &=2,\cr t_1+2t_2&=1. \end{aligned} \] Łatwo sprawdzić, że układ ten jest niespójny i nie ma rozwiązania. Rzeczywiście, rozwiązaliśmy już wcześniej układ składający się z dwóch pierwszych równań(\(t_1=\frac 54\) and \(t_2=-\frac 12\)), a ostatnie równanie jest sprzeczne z tymi wartościami (\(\frac 54+2\cdot(-\frac 12)\neq 1\)).
Rozwiązywanie niespójnych układów równań
Wprowadźmy teraz rozsądne uogólnienie tego, co uważamy za rozwiązanie. Zamiast szukać wartości niewiadomych, które sprawią, że lewa i prawa strona będą dokładnie równe, będziemy szukać wartości, które sprawią, że obie strony będą jak najbliżej siebie.
Przez rozwiązanie niespójnego układu równań będziemy rozumieć taki wybór niewiadomych, dla którego długość wektora wyrażającego różnicę między lewą i prawą stroną układu jest minimalna. Załączony rysunek pomaga nam zrozumieć, co reprezentuje ten system i jak zwizualizować jego rozwiązanie w osłabionym sensie opisanym powyżej.
Ta kombinacja jest reprezentowana przez wektor \(\vec w_0\), a różnica między \(\vec w\) i \(\vec w_0\) jest reprezentowana przez wektor \(\vec \varepsilon\). Naszym celem jest, aby długość wektora \(\vec \varepsilon\) była jak najmniejsza.
Z wizualnego punktu widzenia i właściwości geometrycznych łatwo zauważyć, że dzieje się tak, gdy wektor \(\vec \varepsilon\) jest prostopadły do płaszczyzny wyznaczonej przez wektory \(\vec u_1\) i \(\vec u_2\). To prowadzi nas do tej samej sytuacji, którą napotkaliśmy w alternatywnym rozwiązaniu zadania 3. Tam również użyliśmy sztuczki, aby znaleźć współczynniki \(\vec u_1\) i \(\vec u_2\) bez rozwiązywania pełnego układu równań - wzięliśmy iloczyn kropkowy układu z wektorami \(\vec u_1\) i \(\vec u_2\). W rzeczywistości do tych obliczeń nie potrzebowaliśmy nawet znać wektora \(\vec \varepsilon\).
Ponieważ długość wektora \(\vec \varepsilon\) jest wyrażona w postaci kwadratów jego składowych, metoda ta nazywana jest metodą najmniejszych kwadratów.
Zademonstrujemy całą procedurę na poniższym przykładzie.
Regresja liniowa
Rozważmy dane w poniższej tabeli:
| \(x\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|
| \(y\) | \(1\) | \(5\) | \(7\) |
Szukamy linii \(y=ax+b\), która najlepiej oddaje trend w tym zbiorze danych i służy jako odpowiedni model matematyczny dla danych. Podstawiając każdy z trzech punktów do równania prostej, otrzymujemy układ trzech równań z dwiema niewiadomymi. \[ \begin{aligned} 2a+b=1\cr 3a+b=5\cr 4a+b=7 \end{aligned} \] Jest to układ równań, który jest niespójny - znany również jako układ nadmiernie zdeterminowany - i nie ma rozwiązania w klasycznym sensie. Postać wektorowa układu to: \[ a \begin{pmatrix}2\\3\\4\end{pmatrix} + b \begin{pmatrix}1\\1\\1\end{pmatrix} = \begin{pmatrix}1\\5\\7\end{pmatrix} \] Biorąc iloczyn skalarny obu stron z wektorami \(\begin{pmatrix}2\\3\\4\end{pmatrix}\) i \(\begin{pmatrix}1\\1\\1\end{pmatrix}\) otrzymujemy następujący układ dwóch równań: \[ \begin{aligned} 29a+9b&=45\\ 9a+3b&=13 \end{aligned} \] Rozwiązaniem tego układu jest \(a=3\) i \(b=-\frac {14}3\). Modelem regresji dla podanych danych jest zatem linia \[y=3x-\frac {14}3.\] Wykres zawierający podane dane i linię regresji przedstawiono na rysunku.
Regresja dla większych zestawów danych
Procedurę opisaną w poprzedniej sekcji dla trzech punktów można uogólnić na dowolną liczbę punktów. Nierzadko zdarza się pracować z zestawami danych zawierającymi setki punktów.
Jeśli wektor \(\vec X\) zawiera wartości zmiennej niezależnej 1 , a wektor \(\vec Y\) zawiera wartości zmiennej zależnej, rozważamy model2 \[ \vec Y = a\vec X+b. \] Wyznaczamy współczynniki \(a\) i \(b\) przepisując to równanie jako równanie wektorowe: \[ \vec Y = a\vec X+b\vec 1, \] gdzie \(\vec 1\) jest wektorem składającym się z jedynek. Następnie bierzemy iloczyn kropkowy obu stron z wektorami \(\vec X\) i \(\vec 1\). W ten sposób otrzymujemy układ: \[ \begin{aligned} a(\vec X\cdot \vec X)+ b(\vec X\cdot \vec 1) &= \vec X\cdot \vec Y \cr a(\vec 1\cdot \vec X)+ b(\vec 1\cdot \vec 1) &= \vec 1\cdot \vec Y \cr \end{aligned}\tag{3} \]
Podczas pracy z więcej niż trzema punktami mamy do czynienia z wektorami o wymiarze większym niż trzy. W rezultacie tracimy wizualną interpretację geometryczną. Poza tym procedura pozostaje niezmieniona. Iloczyn skalarny dwóch wektorów jest nadal obliczany przez pomnożenie odpowiednich składników, a następnie zsumowanie iloczynów.
Zadanie 4. Znajdź odpowiedni model liniowy dla tabeli danych z sekcji wprowadzającej.
Rozwiązanie. Przypomnijmy sobie podane dane:
| wzrost/m | \(1{,}47\) | \(1{,}52\) | \(1{,}57\) | \(1{,}63\) | \(1{,}68\) | \(1{,}73\) | \(1{,}78\) | \(1{,}83\) |
|---|---|---|---|---|---|---|---|---|
| waga/kg | \(52{,}21\) | \(54{,}48\) | \(57{,}20\) | \(59{,}93\) | \(63{,}11\) | \(66{,}28\) | \(69{,}92\) | \(74{,}46\) |
Podstawiając dane do niezbędnych iloczynów kropkowych, otrzymujemy:
\[ \begin{aligned} \vec X\cdot\vec X&= 1{,}47^2 + 1{,}52^2+1{,}57^2+\cdots+1{,}83^2=21{,}9257\cr \vec X\cdot\vec Y&= 1{,}47 \cdot 52{,}21 + 1{,}52\cdot 54{,}48 + 1{,}57\cdot 57{,}20+\cdots+ 1{,}83\cdot 74{,}46=828{,}4568\cr \vec 1\cdot\vec X&= 1{,}47 + 1{,}52+ 1{,}57+\cdots+ 1{,}83= 13{,}21\cr \vec 1\cdot\vec Y&= 52{,}21 + 54{,}48+57{,}20+\cdots+74{,}46=497{,}59\cr \vec 1\cdot\vec 1 &= 1+1+1+\cdots +1=8 \end{aligned} \]
Podstawiając te wartości do układu (3), otrzymujemy układ dwóch równań z dwiema niewiadomymi:
\[ \begin{aligned} 21{,}9257a+13{,}21b&=828{,}4568\cr 13{,}21a+8b&=497{,}59. \end{aligned} \]
Układ ten ma unikalne rozwiązanie:3 \(a=60{,}44\) i \(b=-37{,}61\). Wynikowy model opisujący zależność wagi kobiet \(y\) od ich wzrostu \(x\) to \[ y=60{,}44x-37{,}61. \]
Rysunek 4 przedstawia punkt danych, linię regresji i prognozę dla wagi kobiety o wzroście 1{,}72$ metrów.
Zadanie 5. Znajdź linię regresji dla podanych danych.
| \(x\) | \(1{,}0\) | \(2{,}0\) | \(3{,}0\) | \(4{,}0\) |
|---|---|---|---|---|
| \(y\) | \(2{,}3\) | \(2{,}5\) | \(3{,}1\) | \(3{,}3\) |
Rozwiązanie.
Niech wektory \(\vec X\) i \(\vec Y\) będą dane odpowiednio w pierwszym i drugim wierszu tabeli. Następnie: \[ \begin{aligned} \vec X\cdot\vec X&=1{,}0^2+2{,}0^2+3{,}0^2+4{,}0^2=30;\cr \vec X\cdot\vec Y&=1{,}0\cdot 2{,}3+2{,}0\cdot 2{,}5+3{,}0\cdot 3{,}1+4{,}0\cdot 3{,}3=29{,}8;\cr \vec 1\cdot\vec X&=1{,}0+2{,}0+3{,}0+4{,}0=10;\cr \vec 1\cdot\vec Y&=2{,}3+2{,}5+3{,}1+3{,}3=11{,}2;\cr \vec 1\cdot\vec 1&=1+1+1+1=4. \end{aligned} \]
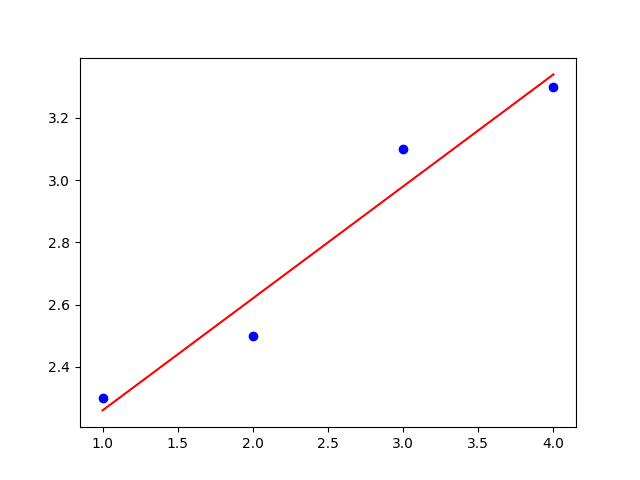
Podstawiając te wartości do układu (3) otrzymujemy: \[ \begin{aligned} 30a+10b&=29{,}8\cr 10a+4b&=11{,}2. \end{aligned} \] Rozwiązanie tego układu daje: \(a=0{,}36\) i \(b=1{,}90\). Linia regresji dla podanych danych ma zatem postać \[y=0{,}36x+1{,}90.\] Rysunek przedstawia linię regresji wraz z punktami danych.
Uwagi końcowe
- W statystyce opisana powyżej metoda jest jednym z podstawowych narzędzi wykorzystywanych do przewidywania, czy jedna zmienna wpływa na wartości innej. Z tego powodu istnieją metody, które oceniają jakość aproksymacji i oceniają, czy wybrany model jest odpowiedni dla danego zestawu punktów danych.
- Istnieją również wielozmienne (wielowymiarowe) wersje metody najmniejszych kwadratów, w których przewidywana wartość zależy nie od jednej, ale od kilku niezależnych zmiennych.
- Problem rozwiązywania niespójnego układu równań liniowych pojawia się również w rekonstrukcji obrazu w tomografii akustycznej. Pozwala to na badanie składu warstw geologicznych lub stanu drewna lub drzewa na podstawie informacji o prędkości, z jaką fale odkształceń sprężystych przechodzą przez materiał. Seria artykułów na blogu https://tomroelandts.com/ może służyć jako wprowadzenie do zagadnienia.
- Możliwe jest również wyprowadzenie bezpośrednich wzorów do obliczania współczynników regresji liniowej z podanych danych - takie podejście pozwala uniknąć obliczania iloczynów kropkowych i rozwiązywania układów równań. Zobacz na przykład https://en.wikipedia.org/wiki/Simple_linear_regression#Expanded_formulas.
Literatura i odniesienia
Literatura
- Wikipedie, Simple linear regression, https://en.wikipedia.org/wiki/Simple_linear_regression, 12.4.2024
- Tom Roelandts, https://tomroelandts.com/articles/tomography-part-1-projections, https://tomroelandts.com/articles/the-sirt-algorithm, 13.4.2024
Źródła danych liczbowych
- https://commons.wikimedia.org/wiki/File:Flag-map_of_the_United_States.svg
Będziemy używać notacji powszechnie stosowanej w przetwarzaniu danych, , w której zbiory danych (wektory) są oznaczane dużymi literami , a wektor, którego wszystkie składowe są równe tej samej liczbie, jest zapisywany jako dana liczba ze strzałką wskazującą wektor.↩︎
Ściśle mówiąc, operacja ta nie ma sensu matematycznego, ponieważ dodajemy wektor do liczby rzeczywistej. Ta operacja musi być interpretowana składniowo, gdzie to dodawanie oznacza, że liczba rzeczywista jest zmieniana na wektor o odpowiednim wymiarze, aby operacja była zdefiniowana. Adaptację tę nazywamy broadcasting. W rezultacie dodajemy wartość \(b\) do każdej składowej wektora \(a\vec X\).↩︎
Uwaga, zadanie jest dość wrażliwe na zaokrąglenia.↩︎