In practice, we often find that the values of one variable are determined by the values of another variable. From a set of measured or statistically obtained data, we can derive a mathematical model that indicates the functional dependence between the two variables. For example, consider data indicating the height and mass of American women aged 30–39 (source: https://en.wikipedia.org/wiki/Simple_linear_regression, accessed 12 April 2024; only half of the data is shown here for the sake of brevity).
| height/m | \(1{,}47\) | \(1{,}52\) | \(1{,}57\) | \(1{,}63\) | \(1{,}68\) | \(1{,}73\) | \(1{,}78\) | \(1{,}83\) |
|---|---|---|---|---|---|---|---|---|
| mass/kg | \(52{,}21\) | \(54{,}48\) | \(57{,}20\) | \(59{,}93\) | \(63{,}11\) | \(66{,}28\) | \(69{,}92\) | \(74{,}46\) |
The data is displayed in the figure on the left. As can be seen from the figure, weight increases as height increases. In such a case, it is possible to find a mathematical model that gives weight as a function of height. Such a mathematical model is shown in color in the figure on the right. This model allows the mass of a woman to be predicted for a given height.
We call the described method linear regression.
Linear regression is one of the basic methods of machine learning, where we discover a certain functional dependence in the data. This can then be used to predict functional values for data that do not occur in the given set.
In the following, we will show how linear regression is related to linear combinations of vectors, and how the regression line can be found using vector operations. We will proceed in small steps:
Exercise 1. Write the vector \(\vec c = \begin{pmatrix}1 \cr 2\end{pmatrix}\) as a linear combination of the vectors \(\vec a = \begin{pmatrix}2 \cr 2\end{pmatrix}\) and \(\vec b = \begin{pmatrix}3 \cr 1\end{pmatrix}\).
Solution. Writing the vector \(\vec c\) as a combination of the vectors \(\vec a\) and \(\vec b\) means finding the numbers \(t_1\) and \(t_2\) such that \[ t_1 \vec a + t_2 \vec b = \vec c. \] After writing it out in coordinates, we see that this problem leads to the system of equations \[ \begin{aligned} 2t_1+3t_2 &= 1,\cr 2t_1+t_2 &=2. \end{aligned} \] This system has a unique solution \(t_1=\frac 54\) and \(t_2=-\frac 12\).
Exercise 2. Write the vector \(\vec w=\begin{pmatrix}1\cr 2\cr 1\end{pmatrix}\) as a linear combination of the vectors \[ \vec u_1=\begin{pmatrix}2\cr 2\cr 1\end{pmatrix},\quad \vec u_2=\begin{pmatrix}3\cr 1\cr 2\end{pmatrix},\quad \vec u_3=\begin{pmatrix}3\cr -1\cr -4\end{pmatrix}. \]
Solution. Similar to the previous problem, we are looking for the numbers \(t_1\), \(t_2\) and \(t_3\) such that \[ t_1 \vec u_1+t_2\vec u_2 + t_3 \vec u_3 = \vec w.\tag{1} \] After substituting and writing out in coordinates, we get a system of three equations with three unknowns \[\tag{2} \begin{aligned} 2t_1 + 3t_2 + 3t_3 &= 1,\cr 2 t_1 + t_2 -t_3 &=2,\cr t_1+2t_2-4t_3&=1. \end{aligned} \] Solving such a system is already quite unpleasant. However, using the addition or substitution method, we could find that \[ t_1=\frac{14}{13},\quad t_2=-\frac{7}{26},\quad t_3=-\frac{3}{26}. \]
If at least one of the given vectors is perpendicular to the remaining vectors, we can use a clever trick to obtain a simpler system of equations.
Let’s go back to the previous problem. We can notice that the vector \(\vec u_3\) is perpendicular to the vectors \(\vec u_1\) and \(\vec u_2\). Therefore, it is also perpendicular to the plane defined by these vectors. We can easily show this fact by calculating the scalar products \[ \vec u_1\cdot \vec u_3 = 2\cdot 3 +2\cdot (-1)+1\cdot (-4) = 0 \] and \[ \vec u_2\cdot \vec u_3 = 3\cdot 3 +1\cdot (-1)+2\cdot (-4) = 0. \] Thanks to this property, it is worth multiplying equation (1) using dot product by the vectors \(\vec u_1\) to \(\vec u_3\). This gives us the following three equations. \[ \begin{aligned} t_1 (\vec u_1\cdot \vec u_1) + t_2 (\vec u_2\cdot \vec u_1) + t_3 (\vec u_3\cdot \vec u_1) &= \vec w\cdot \vec u_1\cr t_1 (\vec u_1\cdot \vec u_2) + t_2 (\vec u_2\cdot \vec u_2) + t_3 (\vec u_3\cdot \vec u_2) &= \vec w\cdot \vec u_2\cr t_1 (\vec u_1\cdot \vec u_3) + t_2 (\vec u_2\cdot \vec u_3) + t_3 (\vec u_3\cdot \vec u_3) &= \vec w\cdot \vec u_3 \end{aligned} \] By calculating the dot products, we obtain a system that is much simpler than system (2). \[ \begin{aligned} 9t_1+10t_2=7\cr 10t_1+14t_2=7\cr 26t_3=-3 \end{aligned} \] From the last equation we see directly one of the unknowns and the first two equations form a system of two equations with two unknowns \(t_1\) and \(t_2\).
Let us recall that inconsistent are the systems linear equations that have no solution.
We modify our problem of finding the expression of a vector as a linear combination of given vectors. We omit one of the vectors we are working with. This makes the problem unsolvable in the classical sense.
Exercise 3. Write the vector \(\vec w=\begin{pmatrix}1\cr 2\cr 1\end{pmatrix}\) as a linear combination of the vectors \[ \vec u_1=\begin{pmatrix}2\cr 2\cr 1\end{pmatrix},\quad \vec u_2=\begin{pmatrix}3\cr 1\cr 2\end{pmatrix}. \]
Solution. We need to find the numbers \(t_1\), \(t_2\) such that \[t_1\vec u_1 + t_2\vec u_2 = \vec w.\] By writing it out in coordinates, we get the system \[ \begin{aligned} 2t_1 + 3t_2 &= 1,\cr 2 t_1 + t_2 &=2,\cr t_1+2t_2&=1. \end{aligned} \] It is easy to see that this system is inconsistent and has no solution. Indeed, we solved the system consisting of the first two equations in the introduction (\(t_1=\frac 54\) and \(t_2=-\frac 12\)), and the last equation conflicts with this choice (\(\frac 54+2\cdot(-\frac 12)\neq 1\)).
Let’s now generalize the concept of a solution in a reasonable way. We will not look for values of the unknowns for which the left and right sides are equal. Instead, we will look for at least such values of the unknowns for which the left and right sides differ as little as possible.
By the solution of an inconsistent system of equations we will understand the choice of values of the unknowns for which the length of the vector expressing the difference between the left and right sides of the system is minimal.
In the figure, we will explain what the given system expresses and how it is possible to imagine its solution in the weakened sense mentioned above.
This combination is given by the vector \(\vec w_0\), while the difference between \(\vec w\) and \(\vec w_0\) is represented by the vector \(\vec \varepsilon\). We are trying to make the length of the vector \(\vec \varepsilon\) as small as possible.
From a visual point of view and geometric properties, it is easy to see that this occurs in the case when the vector \(\vec \varepsilon\) is perpendicular to the plane defined by the vectors \(\vec u_1\) and \(\vec u_2\). This brings us to the same situation as in the alternative solution to the third problem. There, we also saw a trick for finding the coefficients of the vectors \(\vec u_1\) and \(\vec u_2\) without solving the full system of equations: we multiplied the system using dot product by the vectors \(\vec u_1\) and \(\vec u_2\). We don’t even need to know the vector \(\vec \varepsilon\) for this calculation.
Since the length of the vector \(\vec\varepsilon\) is expressed using the squares of the coordinates of this vector, the method is called the least squares method.
We will show the entire procedure in the following example.
Consider the data from the following table.
| \(x\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|
| \(y\) | \(1\) | \(5\) | \(7\) |
We are looking for a line \(y=ax+b\) that best describes the trend in this set and would be a suitable mathematical model for this data. By substituting each of the three points into the equation of the line, we obtain a system of three equations in two unknowns. \[ \begin{aligned} 2a+b=1\cr 3a+b=5\cr 4a+b=7 \end{aligned} \] This is a problem with an inconsistent system of equations (the so-called overdetermined system), which has no solution in the classical sense. The vector form of this system is as follows. \[ a \begin{pmatrix}2\\3\\4\end{pmatrix} + b \begin{pmatrix}1\\1\\1\end{pmatrix} = \begin{pmatrix}1\\5\\7\end{pmatrix} \] After multiplying the vectors \(\begin{pmatrix}2\\3\\4\end{pmatrix}\) and \(\begin{pmatrix}1\\1\\1\end{pmatrix}\) in turn, we obtain a system of two equations. \[ \begin{aligned} 29a+9b&=45\\ 9a+3b&=13 \end{aligned} \] The solution to this system is \(a=3\) and \(b=-\frac {14}3\). The regression model for the given data is therefore the line \[y=3x-\frac {14}3.\] The graph containing the given data and the regression line is shown in the figure.
The procedure outlined above for three points can be generalized to any number of points. It is not uncommon to work with a dataset containing hundreds of points.
If the vector \(\vec X\) is a vector containing the values of the independent variable1 and \(\vec Y\) is a vector containing the values of the dependent variable, we will consider the model2 \[ \vec Y = a\vec X+b. \] The coefficients \(a\) and \(b\) are determined by rewriting this equation into the vector equation \[ \vec Y = a\vec X+b\vec 1, \] where \(\vec 1\) is a vector composed of ones. We multiply this equation using dot product by the vector \(\vec X\) and the vector \(\vec 1\). We thus get a system \[ \begin{aligned} a(\vec X\cdot \vec X)+ b(\vec X\cdot \vec 1) &= \thing X\cdot \thing Y \cr a(\vec 1\cdot \vec X)+ b(\vec 1\cdot \vec 1) &= \vec 1\cdot \vec Y \cr \end{aligned}\tag{3} \]
For more than three points, we work with vectors of dimension higher than three. As a result, we lose the clear geometric idea. Apart from this, however, the procedure remains the same. The dot product of two vectors is still calculated by multiplying the corresponding components and then adding these products.
Exercise 4. Find a suitable linear model for the data table from the introductory text.
Solution. Let’s recall the given data:
| height/m | \(1{,}47\) | \(1{,}52\) | \(1{,}57\) | \(1{,}63\) | \(1{,}68\) | \(1{,}73\) | \(1{,}78\) | \(1{,}83\) |
|---|---|---|---|---|---|---|---|---|
| mass/kg | \(52{,}21\) | \(54{,}48\) | \(57{,}20\) | \(59{,}93\) | \(63{,}11\) | \(66{,}28\) | \(69{,}92\) | \(74{,}46\) |
After substituting the data into the necessary dot products, we get:
\[ \begin{aligned} \vec X\cdot\vec X&= 1{,}47^2 + 1{,}52^2+1{,}57^2+\cdots+1{,}83^2=21{,}9257\cr \vec X\cdot\vec Y&= 1{,}47 \cdot 52{,}21 + 1{,}52\cdot 54{,}48 + 1{,}57\cdot 57{,}20+\cdots+ 1{,}83\cdot 74{,}46=828{,}4568\cr \vec 1\cdot\vec X&= 1{,}47 + 1{,}52+ 1{,}57+\cdots+ 1{,}83= 13{,}21\cr \vec 1\cdot\vec Y&= 52{,}21 + 54{,}48+57{,}20+\cdots+74{,}46=497{,}59\cr \vec 1\cdot\vec 1 &= 1+1+1+\cdots +1=8 \end{aligned} \]
After substituting the values into (3), we get a system of two equations in two unknowns
\[ \begin{aligned} 21{,}9257a+13{,}21b&=828{,}4568,\cr 13{,}21a+8b&=497{,}59, \end{aligned} \]
which has a single solution. This solution3 is \(a=60{,}44\) and \(b=-37{,}61\). The model that gives the dependence of the weight of women \(y\) on their height \(x\) is the relation \[y=60{,}44x-37{,}61.\]
Figure 4 shows the data used, the regression dependence, and the prediction for the weight of a woman with a height of \(1{,}72\) meters.
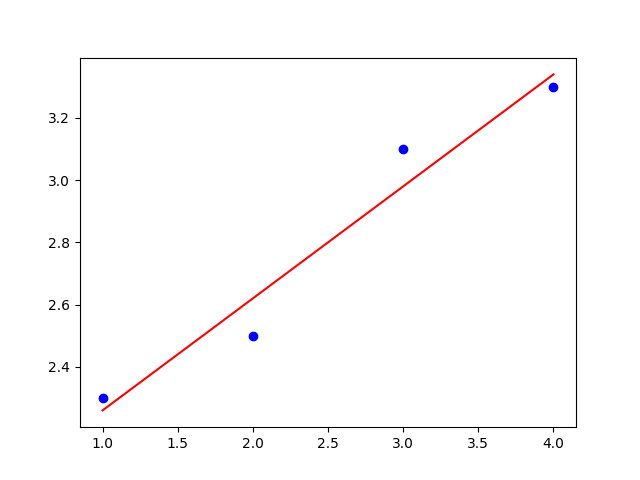
Exercise 5. Find the regression line for the given data.
| \(x\) | \(1{,}0\) | \(2{,}0\) | \(3{,}0\) | \(4{,}0\) |
|---|---|---|---|---|
| \(y\) | \(2{,}3\) | \(2{,}5\) | \(3{,}1\) | \(3{,}3\) |
Solution.
For vectors \(\vec X\) and \(\vec Y\) given respectively by the first and second rows of the table, we obtain \[ \begin{aligned} \vec X\cdot\vec X&=1{,}0^2+2{,}0^2+3{,}0^2+4{,}0^2=30,\cr \vec X\cdot\vec Y&=1{,}0\cdot 2{,}3+2{,}0\cdot 2{,}5+3{,}0\cdot 3{,}1+4{,}0\cdot 3{,}3=29{,}8,\cr \vec 1\cdot\vec X&=1{,}0+2{,}0+3{,}0+4{,}0=10,\cr \vec 1\cdot\vec Y&=2{,}3+2{,}5+3{,}1+3{,}3=11{,}2,\cr \vec 1\cdot\vec 1&=1+1+1+1=4. \end{aligned} \]
The system of equations (3) after substituting these values has the form \[ \begin{aligned} 30a+10b&=29{,}8,\cr 10a+4b&=11{,}2. \end{aligned} \] The solution to this system is \(a=0{,}36\) and \(b=1{,}90\). The regression line for the given data is therefore \[y=0{,}36x+1{,}90.\] The figure shows the regression line and the given data.
We will use a notation commonly used in data processing, where data sets (vectors) are denoted by capital letters and a vector that has all components equal to the same number is written as a given number with an arrow to indicate the vector.↩︎
Strictly speaking, this operation does not make mathematical sense, because we are adding a vector to a real number. This operation must be interpreted component-wise, where this addition means that the real number is changed to a vector of the appropriate dimension so that the operation is defined. We call this adaptation broadcasting. As a result, we add the value \(b\) to each component of the vector \(a\vec X\).↩︎
Be careful, the exercise is quite sensitive to rounding.↩︎