Wieże chłodnicze elektrowni to monumentalne konstrukcje wykonane z betonu, wznoszące się ku niebu i emitujące białe chmury pary wodnej. Te żelbetowe skorupy, zbudowane na cienkich, dziesięciometrowych nogach, stanowią integralną część technologii elektrowni. Każda wieża chłodnicza ma moc cieplną ponad \(1{,}000\,\text{MW,}\). Oznacza to, że co godzinę do powietrza uwalniana jest ilość ciepła wystarczająca do ogrzania około osiemdziesięciu domów przez cały rok.
Wieża chłodnicza elektrowni jądrowej Temelín ma kształt hiperboloidy obrotowej z jednym arkuszem. Od wysokości dwudziestu metrów do szczytu na wysokości \(155\,\text{m}\), wnętrze wieży jest całkowicie puste. Ta żelbetowa skorupa ma grubość 90,$ w dolnej części wieży, tylko trzy razy grubszą niż betonowa płyta fundamentowa domu jednorodzinnego. Grubość stopniowo maleje w górę, a w koronie powłoka jest tak szeroka jak koło samochodu (około \(18\,\text{cm}\)). Cała powłoka zbudowana jest na około stu betonowych nogach, tworzących wloty powietrza. Okrągły basen pod wieżą (podobnie jak sama wieża) ma średnicę około \(130\,\text{m}\).
Naszym zadaniem jest określenie objętości chłodni kominowej elektrowni jądrowej Temelín. Zadanie to wykonamy krok po kroku. Najpierw znajdziemy funkcję modelującą wieżę, a następnie określimy jej objętość za pomocą całki oznaczonej.
Aby uprościć obliczenia, nieco idealizujemy rzeczywistą wieżę chłodniczą (zaokrąglamy niektóre wymiary). Załóżmy, że wieża ma kształt części hiperboloidy z jednego arkusza o wysokości \(155\,\text{m}\), promieniu podstawy \(65\,\text{m}\) i promieniu korony \(41\,\text{m}\). Jego najwęższy punkt znajduje się 35,$ poniżej korony chłodni kominowej. Aby pracować ze współrzędnymi, jak jesteśmy przyzwyczajeni, umieścimy oś hiperboloidy obrotowej tak, aby pokrywała się z osią współrzędnych \(x\). Co więcej, umieścimy ją tak, aby przekrój wieży chłodniczej wzdłuż jej osi tworzył część hiperboli, z podstawą wieży znajdującą się w punkcie \([155, 65]\) i wierzchołkiem (koroną) w punkcie \([0, 41]\). Ponieważ najwęższa część wieży znajduje się \(35\,\text{m}\) poniżej korony wieży chłodniczej, środek hiperboli ma współrzędne \([35, 0]\). Wieżę chłodniczą można utworzyć, obracając część tej hiperboli wokół osi \(x\).
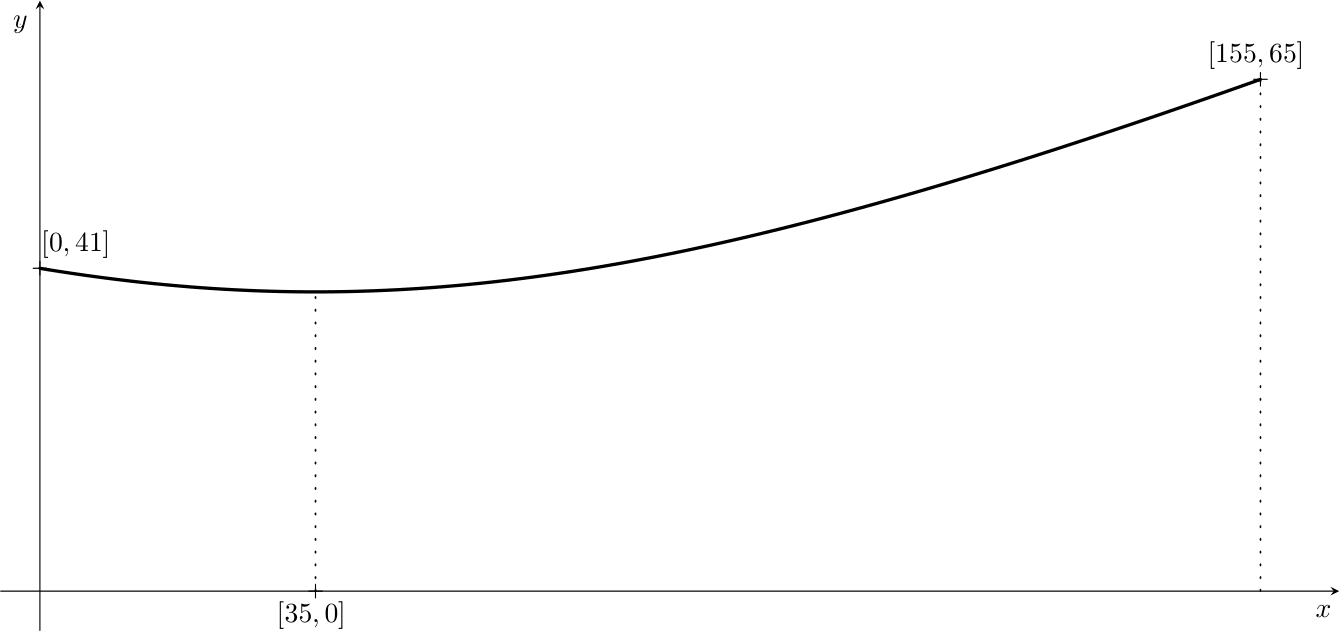
Zadanie 1. Napisz w standardowej formie równanie hiperboli o środku \([35, 0]\) i ogniskach leżących na osi równoległej do osi \(x\).
Rozwiązanie. Standardowa postać równania hiperboli to \[\frac{y^2}{a^2} - \frac{(x - 35)^2}{b^2} = 1.\]
Zadanie 2. Wyznacz standardową postać równania hiperboli, której częścią jest przekrój wieży, biorąc pod uwagę, że leżą na niej punkty \([155, 65]\) i \([0, 41]\). Zastąp wartości zaokrąglone do najbliższej liczby całkowitej dla \(a^2\), \(b^2\) w równaniu.
Rozwiązanie. Po podstawieniu punktów \([155, 65]\), \([0, 41]\) leżących na hiperboli otrzymujemy układ równań \[ \begin{align*} \frac{65^2}{a^2} - \frac{(155-35)^2}{b^2} &= 1 \\ \frac{41^2}{a^2} - \frac{35^2}{b^2} &= 1 \\ \end{align*} \] Wyrażenie \(\frac{1}{a^2}\) z pierwszego równania \[\frac{1}{a^2}=\frac{1}{65^2}\left(1+\frac{120^2}{b^2}\right)\] i podstawiając ją do drugiego równania, otrzymujemy \[\frac{41^2}{65^2}\left(1+\frac{120^2}{b^2}\right)-\frac{35^2}{b^2} = 1.\] Teraz rozwiązujemy dla \(b^2\): \[b^2 = \frac{41^2 \cdot 120^2 - 35^2 \cdot 65^2}{65^2-41^2} \;\dot{=}\; 7{,}481.\] Po podstawieniu z powrotem otrzymujemy \[a^2= \frac{41^2 \cdot 120^2 - 35^2 \cdot 65^2}{120^2-35^2} \;\dot{=}\; 1{,}444.\] Hiperbola modelująca przekrój wieży chłodniczej ma standardową postać równania \[\frac{y^2}{1{,}444} - \frac{(x - 35)^2}{7{,}481} = 1.\]
Zadanie 3. Na podstawie standardowej postaci równania hiperboli wyraź funkcję opisującą gałąź hiperboli leżącą nad osią \(x\).
Rozwiązanie. Ze standardowej postaci równania hiperboli \[\frac{y^2}{1{,}444} - \frac{(x - 35)^2}{7{,}481} = 1\]. wyrażamy \(y\) \[y(x) = \pm\sqrt{1{,}444 + \frac{1{,}444}{7{,}481} (x - 35)^2}.\] Gałąź hiperboli leżąca powyżej osi \(x\) jest opisana funkcją \[y(x) = \sqrt{1{,}444 + \frac{1{,}444}{7{,}481} (x - 35)^2}.\]
Zadanie 4. Obliczyć objętość bryły obrotowej powstałej przez obrót części gałęzi hiperboli modelującej chłodnię kominową w przedziale \(x\in\langle 0, 155\rangle\) wokół osi \(x\).
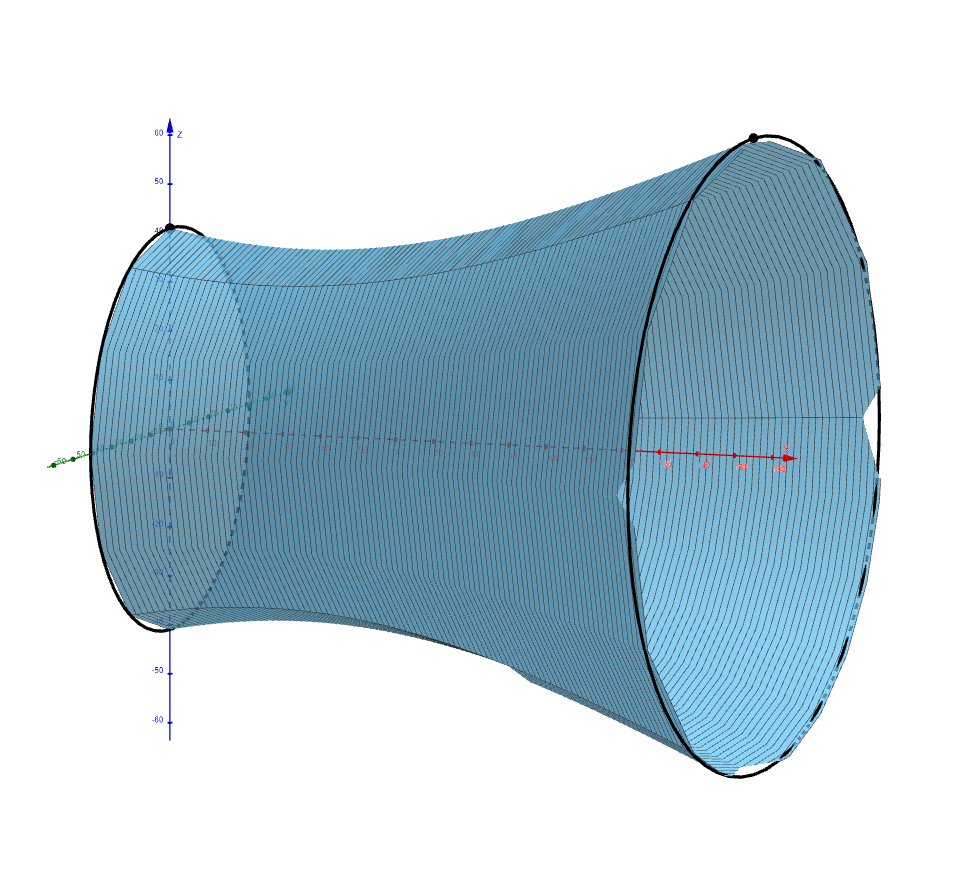
Rozwiązanie. Aby obliczyć objętość, używamy całki oznaczonej wyrażającej objętość bryły obrotowej \[V = \pi \int_{0}^{155} \left(1{,}444 + \frac{1{,}444}{7{,}481} (x - 35)^2\right) \,\mathrm{d}x= \pi \left[1{,}444x + \frac{1{,}444}{7{,}481} \cdot \frac{1}{3}(x - 35)^3 \right]_{0}^{155}\doteq1{,}052{,}436\,\text{m}^3\] Objętość modelu chłodni kominowej elektrowni jądrowej Temelín wynosi 1{,}052{,}436,^3$.
Uwaga. Jeśli porównamy uzyskaną objętość 1{,}052{,}436,^3$ modelu wieży chłodniczej z objętością 1{,}069{,}700,^3$ rzeczywistej wieży chłodniczej w Temelínie, zobaczymy, że nasz wynik jest całkiem realistyczny.