Objem chladící věže jaderné elektrárny
 20 min.,
20 min.,  2/3
2/3 Chladicí věže elektrárny jsou monumentální stavby z betonu, tyčící se k nebi a vypouštějící bílá oblaka vodní páry. Tyto železobetonové skořápky postavené na tenkých desetimetrových nožičkách jsou nedílnou součástí technologie elektrárny. Každá chladicí věž má tepelný výkon přes \(1\,000\, \text{MW,}\) což znamená, že každou hodinu se do ovzduší uvolní tolik tepla, kolik by stačilo k vytápění zhruba osmdesáti domácností po dobu 1 roku.
Chladicí věž jaderné elektrárny Temelín je tvaru jednodílného rotačního hyperboloidu. Od výšky dvaceti metrů až po vrchol ve výšce \(155\,\text{m}\) je uvnitř věže jen prázdný prostor. Tloušťka této železobetonovité skořepiny je v dolní části věže \(90\,\text{cm}\), což je jen dvojnásobek tloušťky obvodové nosné zdi v cihlovém rodinném domě. Směrem nahoru se postupně zmenšuje a u koruny je plášť široký jako kolo osobního auta (asi \(18\,\text{cm}\)). Celý plášť je postaven na asi stovce betonových noh, tvořících vstupní otvory pro nasávání vzduchu. Kruhový bazén pod věží má (stejně jako věž ve spodní části) průměr přibližně \(130\,\text{m}\).

Zadání
Naším úkolem bude určit objem chladící věže jaderné elektrárny Temelín. Na tento úkol půjdeme postupně. V první řadě najdeme funkci pomocí které budeme věž modelovat a následně určíme pomocí určitého integrálu její objem.
Pro zjednodušení výpočtů si skutečnou chladící věž mírně zidealizujeme (zaokrouhlíme některé rozměry). Budeme
o ní předpokládat, že má tvar části hyperboloidu s výškou \(155\,\text{m}\), poloměrem základny \(65\,\text{m}\) a poloměrem koruny \(41\,\text{m}\) . Jeho nejužší místo je \(35\,\text{m}\) pod korunou chladicí věže.
Abychom mohli pracovat v souřadnicích, jak jsme zvyklí, umístíme osu rotačního hyperboloidu tak, aby splývala se souřadnou osou \(x\). Navíc si jej umístíme tak, že řezem chladící věže vedeným jeho osou je část hyperboly, na které leží pata věže se souřadnicemi \([155, 65]\) a vrchol koruny \([0, 41]\). Jelikož nejužší místo věže je \(35\,\text{m}\) pod korunou chladicí věže, má střed hyperboly souřadnice \([35, 0]\). Chladící věž vznikne rotací části této hyperboly kolem osy \(x\).
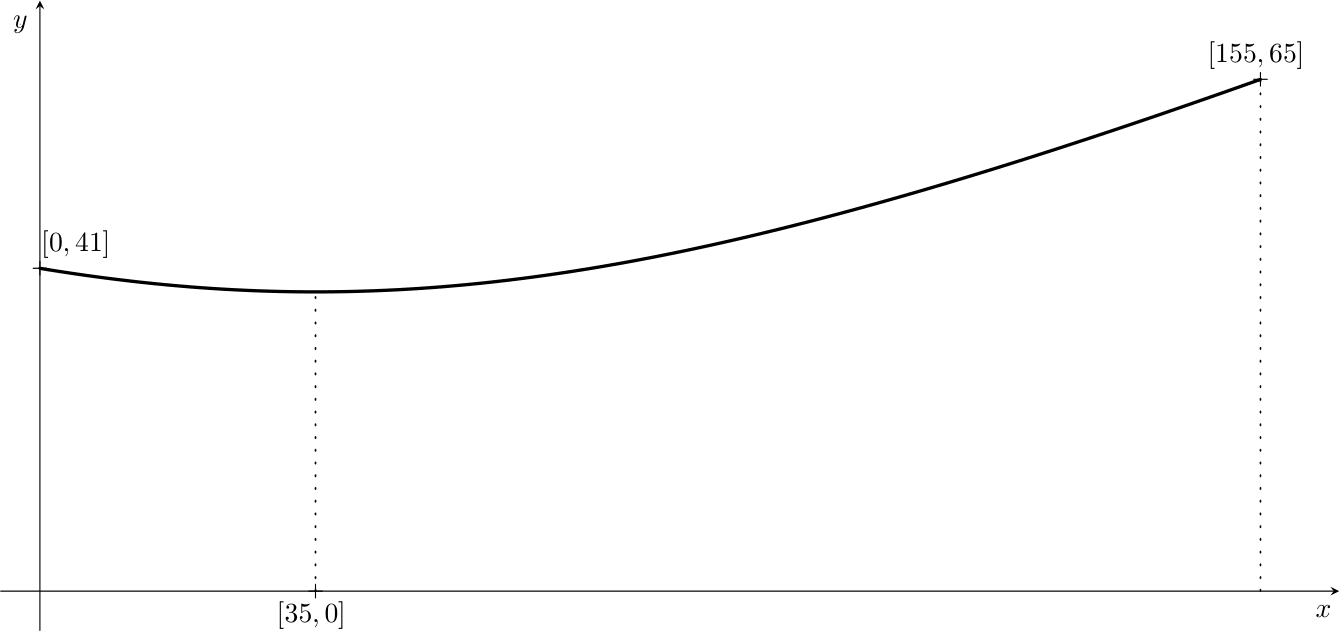
Úloha 1. Napište obecnou rovnici hyperboly se středem \([35, 0]\) a s ohnisky ležícími na ose rovnoběžné s osou \(x\).
Řešení. Obecná rovnice hyperboly má tvar \[\frac{y^2}{a^2} - \frac{(x - 35)^2}{b^2} = 1.\]
Úloha 2. Určete obecnou rovnici hyperboly, jejíž částí je řez chladící věže, jestliže na ní leží body \([155, 65]\) a \([0, 41]\). Do vztahu dosaďte za \(a^2\), \(b^2\) hodnoty zaokrouhlené na jednotky.
Řešení. Po dosazení bodů \([155, 65]\), \([0, 41]\) ležících na hyperbole dostáváme soustavu rovnic \[ \begin{align*} \frac{65^2}{a^2} - \frac{(155-35)^2}{b^2} &= 1 \\ \frac{41^2}{a^2} - \frac{35^2}{b^2} &= 1 \\ \end{align*} \] Vyjádřením \(\frac{1}{a^2}\) z první rovnice \[\frac{1}{a^2}=\frac{1}{65^2}\left(1+\frac{120^2}{b^2}\right)\] a dosazením do druhé rovnice získáme \[\frac{41^2}{65^2}\left(1+\frac{120^2}{b^2}\right)-\frac{35^2}{b^2} = 1.\] Nyní vypočítáme \(b^2\): \[b^2 = \frac{41^2 \cdot 120^2 - 35^2 \cdot 65^2}{65^2-41^2} \;\dot{=}\; 7481.\] Po zpětném dosazení získáme \[a^2= \frac{41^2 \cdot 120^2 - 35^2 \cdot 65^2}{120^2-35^2} \;\dot{=}\; 1444.\] Hyperbola modelující řez chladící věží má obecnou rovnici \[\frac{y^2}{1444} - \frac{(x - 35)^2}{7481} = 1.\]
Úloha 3. Vyjádřete z obecné rovnice hyperboly funkci, která popisuje rameno hyperboly ležící nad osou \(x\).
Řešení. Z obecné rovnice hyperboly \[\frac{y^2}{1444} - \frac{(x - 35)^2}{7481} = 1\] vyjádříme \(y\) \[y(x) = \pm\sqrt{1444 + \frac{1444}{7481} (x - 35)^2}.\] Rameno hyperboly ležící nad osou \(x\) popisuje funkce \[y(x) = \sqrt{1444 + \frac{1444}{7481} (x - 35)^2}.\]
Úloha 4. Vypočítejte objem rotačního tělesa vzniklého rotací části ramena hyperboly modelující chladící věž v intervalu \(x\in\langle 0, 155\rangle\) kolem osy \(x\).
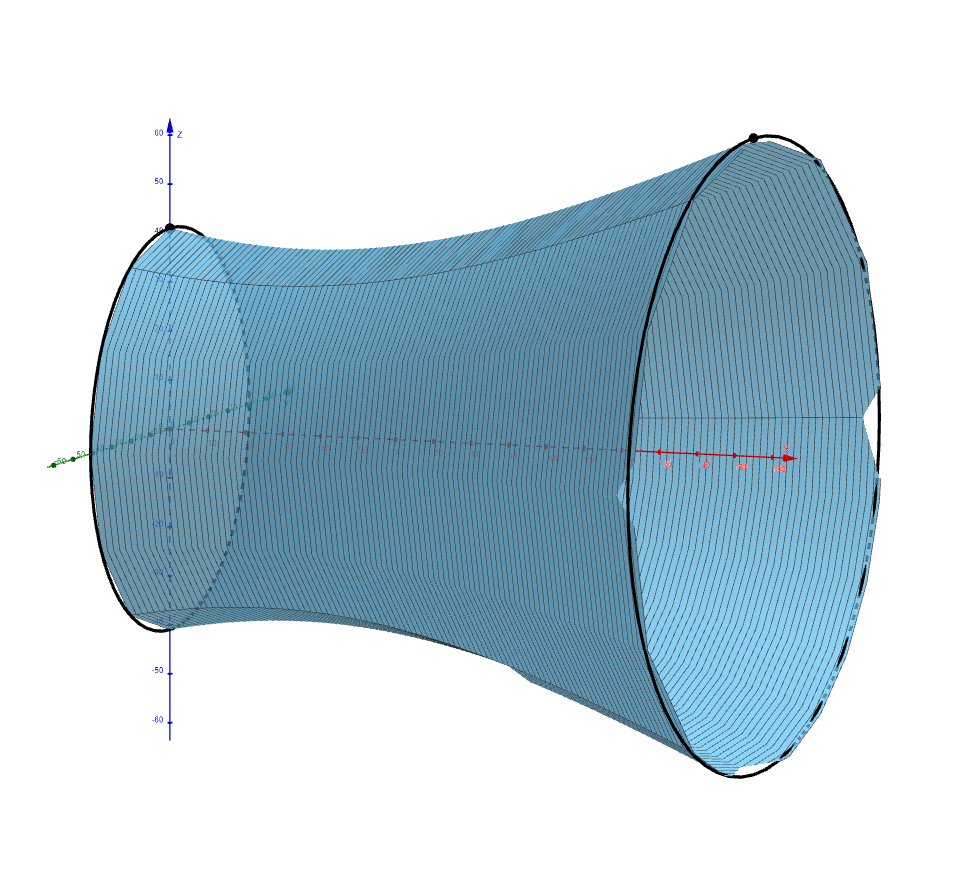
Řešení. K výpočtu objemu použijeme určitý integrál vyjadřující objem rotačního tělesa \[V = \pi \int_{0}^{155} \left(1444 + \frac{1444}{7481} (x - 35)^2\right) \,\mathrm{d}x= \pi \left[1444x + \frac{1444}{7481} \cdot \frac{1}{3}(x - 35)^3 \right]_{0}^{155}\doteq1\,052\,436\,\text{m}^3\] Objem modelu chladící věže jaderné elektrárny Temelín je \(1\,052\,436\,\text{m}^3\).
Poznámka. Porovnáme-li získaný objem \(1\,052\,436\,\text{m}^3\) modelu chladící věže s objemem \(1\,069\,700\,\text{m}^3\) skutečné chladící věže v Temelíně, vidíme, že náš výsledek je velmi realistický.
Literatura
- Wikipedie. Temelín – technologie a zabezpečení [online]. Dostupné z https://www.cez.cz/cs/o-cez/vyrobni-zdroje/jaderna-energetika/jaderna-energetika-v-ceske-republice/ete/technologie-a-zabezpeceni-1 [cit. 28.,11.,2023].
- ČEZ. Chladící věž – jak to funguje [online]. Dostupné z https://www.svetenergie.cz/cz/energetika-zblizka/jaderne-elektrarny-pro-deti/co-vsechno-v-jaderne-elektrarne-najdeme/chladici-vez/jak-to-funguje [cit. 28.,11.,2023].
- Hochtief. Chladící věž – obrázek [online]. Dostupné z https://www.hochtief.cz/nase-projekty/referencni-projekty/prumyslove/temelin-sekundarni-ochrana-vnejsiho-plaste-chladicich-vezi-na-jaderne-elektrarne-temelin [cit. 28.,11.,2023].