Volumen de una torre de refrigeración de una central nuclear
 20 min.,
20 min.,  2/3
2/3 Las torres de refrigeración de la central eléctrica son estructuras monumentales de hormigón, que se elevan hacia el cielo y emiten nubes blancas de vapor de agua. Estas cáscaras de hormigón armado, construidas sobre delgadas patas de diez metros, son una parte integral de la tecnología de la central. Cada torre de refrigeración tiene una potencia térmica superior a \(1{,}000,\text{MW}\). Esto significa que cada hora se libera al aire suficiente calor como para calentar unas ochenta viviendas durante todo un año.
La torre de refrigeración de la central nuclear de Temelín tiene la forma de un hiperboloide de revolución de una hoja. Desde una altura de veinte metros hasta la parte superior, a \(155,\text{m}\), el interior de la torre está completamente hueco. Esta cáscara de hormigón armado tiene un grosor de \(90,\text{cm}\) en la parte inferior de la torre, solo tres veces más gruesa que una losa de cimentación de una casa unifamiliar. El grosor disminuye gradualmente hacia arriba y, en la corona, la cáscara tiene el ancho de una rueda de coche (unos \(18,\text{cm}\)). Toda la cáscara está construida sobre unas cien patas de hormigón, que forman entradas de aire. La piscina circular situada debajo de la torre (al igual que la torre misma) tiene un diámetro de aproximadamente \(130,\text{m}\).

Tarea
Nuestra tarea es determinar el volumen de la torre de refrigeración de la central nuclear de Temelín. Abordaremos esta tarea paso a paso. Primero, encontraremos una función que modele la torre y luego determinaremos su volumen utilizando una integral definida.
Para simplificar los cálculos, idealizamos ligeramente la torre de refrigeración real (redondeamos algunas dimensiones). Supongamos que la torre tiene la forma de una parte de un hiperboloide de una hoja, con una altura de \(155,\text{m}\), un radio en la base de \(65,\text{m}\) y un radio en la corona de \(41,\text{m}\). Su punto más estrecho se encuentra a \(35,\text{m}\) por debajo de la corona de la torre de refrigeración.
Para trabajar con coordenadas, como estamos acostumbrados, colocaremos el eje del hiperboloide de revolución de modo que coincida con el eje de coordenadas \(x\). Además, lo situamos de forma que la sección transversal de la torre de refrigeración a lo largo de su eje forme parte de una hipérbola, con la base de la torre ubicada en el punto \([155, 65]\) y la parte superior (la corona) en \([0, 41]\). Dado que la parte más estrecha de la torre se encuentra a \(35,\text{m}\) por debajo de la corona, el centro de la hipérbola tiene coordenadas \([35, 0]\). La torre de refrigeración se puede generar rotando una parte de esta hipérbola alrededor del eje \(x\).
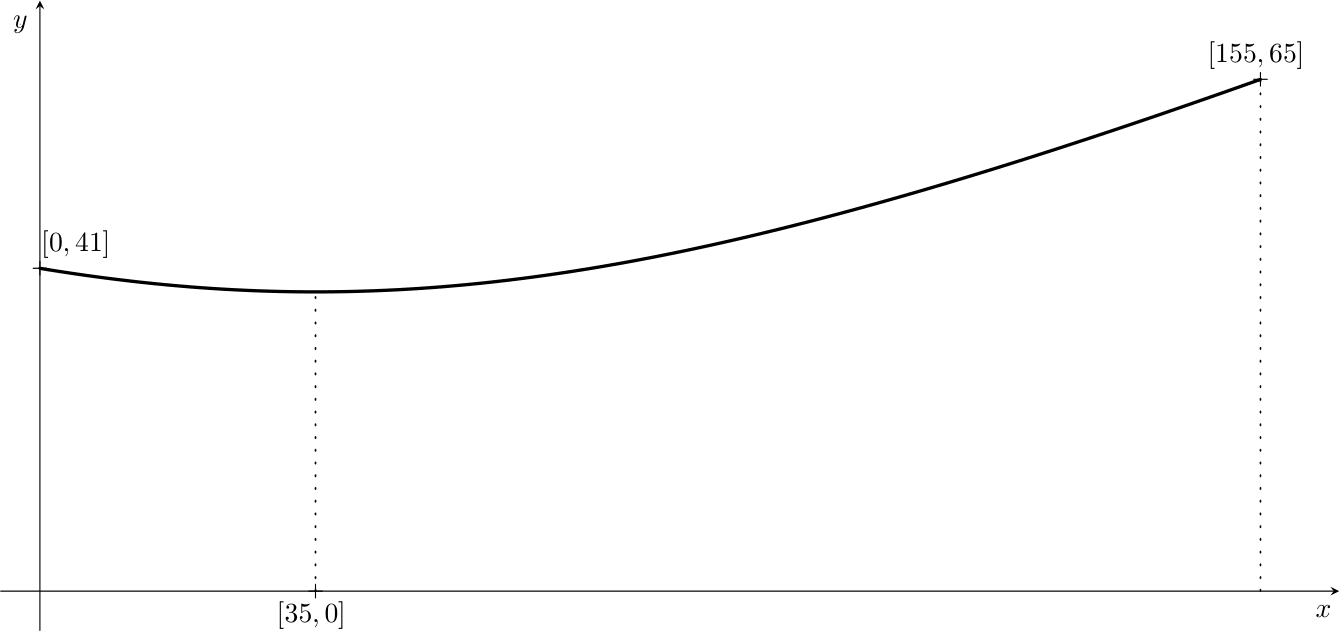
Ejercicio 1. Escribe la forma estándar de la ecuación de una hipérbola con centro en \([35, 0]\) y focos situados sobre un eje paralelo al eje \(x\).
Solución. La forma estándar de la ecuación de una hipérbola es: \[\frac{y^2}{a^2} - \frac{(x - 35)^2}{b^2} = 1.\]
Ejercicio 2. Determina la forma estándar de la ecuación de la hipérbola, de la cual la sección de la torre de refrigeración es una parte, dado que los puntos \([155, 65]\) y \([0, 41]\) pertenecen a ella. Sustituye los valores redondeados al número entero más cercano para \(a^2\) y \(b^2\) en la ecuación.
Solución. Después de sustituir los puntos \([155, 65]\), \([0, 41]\) que se encuentran sobre la hipérbola, obtenemos el sistema de ecuaciones: \[ \begin{align*} \frac{65^2}{a^2} - \frac{(155-35)^2}{b^2} &= 1 \\ \frac{41^2}{a^2} - \frac{35^2}{b^2} &= 1 \\ \end{align*} \] Expresando \(\frac{1}{a^2}\) de la primera ecuación \[\frac{1}{a^2}=\frac{1}{65^2}\left(1+\frac{120^2}{b^2}\right)\] y al sustituirlo en la segunda ecuación, obtenemos: \[\frac{41^2}{65^2}\left(1+\frac{120^2}{b^2}\right)-\frac{35^2}{b^2} = 1.\] Ahora resolvemos para \(b^2\): \[b^2 = \frac{41^2 \cdot 120^2 - 35^2 \cdot 65^2}{65^2-41^2} \;\dot{=}\; 7{,}481.\] Después de volver a sustituir, obtenemos \[a^2= \frac{41^2 \cdot 120^2 - 35^2 \cdot 65^2}{120^2-35^2} \;\dot{=}\; 1{,}444.\] La hipérbola que modela la sección de una torre de refrigeración tiene la forma estándar de la ecuación \[\frac{y^2}{1{,}444} - \frac{(x - 35)^2}{7{,}481} = 1.\]
Ejercicio 3. A partir de la forma estándar de la ecuación de la hipérbola, expresa la función que describe la rama de la hipérbola situada sobre el eje \(x\).
Solución. A partir de la forma estándar de la ecuación de la hipérbola \[\frac{y^2}{1{,}444} - \frac{(x - 35)^2}{7{,}481} = 1\] expresamos \(y\) \[y(x) = \pm\sqrt{1{,}444 + \frac{1{,}444}{7{,}481} (x - 35)^2}.\] La rama de la hipérbola situada por encima del eje \(x\) está descrita por la función: \[y(x) = \sqrt{1{,}444 + \frac{1{,}444}{7{,}481} (x - 35)^2}.\]
Ejercicio 4. Calcula el volumen del sólido de revolución formado al rotar una parte de la rama de la hipérbola que modela la torre de refrigeración en el intervalo: \(x\in\langle 0, 155\rangle\) alrededor del eje \(x\)
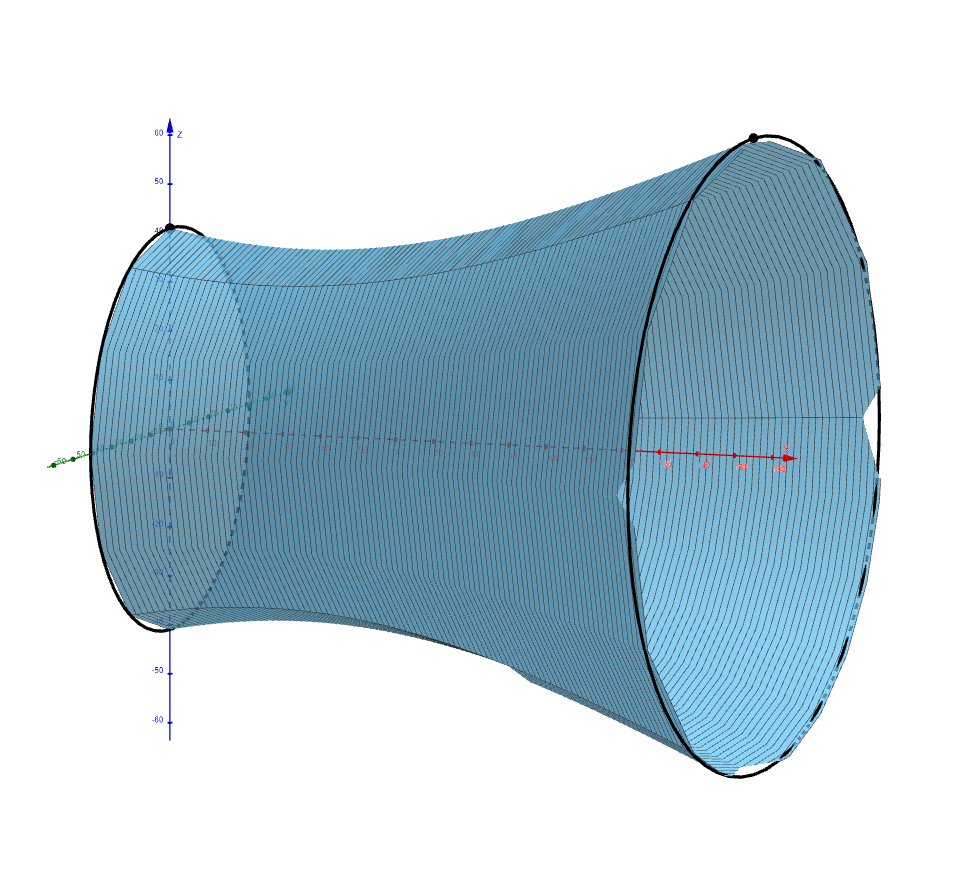
Solución. Para calcular el volumen, utilizamos una integral definida que expresa el volumen de un sólido de revolución \[V = \pi \int_{0}^{155} \left(1{,}444 + \frac{1{,}444}{7{,}481} (x - 35)^2\right) \,\mathrm{d}x= \pi \left[1{,}444x + \frac{1{,}444}{7{,}481} \cdot \frac{1}{3}(x - 35)^3 \right]_{0}^{155}\doteq1{,}052{,}436\,\text{m}^3\] El volumen del modelo de la torre de refrigeración de la central nuclear de Temelín es de \(1{,}052{,}436\,\text{m}^3\).
Nota. Si comparamos el volumen obtenido de \(1{,}052{,}436,\text{m}^3\) del modelo de la torre de refrigeración con el volumen de \(1{,}069{,}700,\text{m}^3\) de la torre de refrigeración real en Temelín, vemos que nuestro resultado es bastante realista.
Bibliografía
- Wikipedie. Temelín – technologie a zabezpečení [online]. Accesible de https://www.cez.cz/cs/o-cez/vyrobni-zdroje/jaderna-energetika/jaderna-energetika-v-ceske-republice/ete/technologie-a-zabezpeceni-1 [cit. 28.,11.,2023].
- ČEZ. Chladící věž – jak to funguje [online]. Accesible de https://www.svetenergie.cz/cz/energetika-zblizka/jaderne-elektrarny-pro-deti/co-vsechno-v-jaderne-elektrarne-najdeme/chladici-vez/jak-to-funguje [cit. 28.,11.,2023].
- Hochtief. Chladící věž – obrázek [online]. Accesible de https://www.hochtief.cz/nase-projekty/referencni-projekty/prumyslove/temelin-sekundarni-ochrana-vnejsiho-plaste-chladicich-vezi-na-jaderne-elektrarne-temelin [cit. 28.,11.,2023].