Při studiu přírody hrají neocenitelnou roli matematické modely. Tyto modely otevírají cestu k předpovědím budoucího vývoje, ale plní i další a důležitější role, jak popíšeme v následujícím textu.
Používání ekologických modelů bývá někdy zmiňováno jako fyzikální postupy v ekologii, protože se studuje ekosystém z hlediska vývoje populací a používají se k tomu matematické metody původně odvozené na řešení fyzikálních úloh. Výstupy z modelů poté nesou například následující informace.
Jedním ze základních vztahů v ekosystémech je vztah dravce a kořisti. Tento vztah může být jedinou interakcí v ekosystému, nebo může být doplněn interakcemi dalšími. Důležitost modelování soužití dravce a kořisti si objasníme na následujících historicky významných modelech.
V roce 1926 publikoval jeden z prvních modelů dravce a kořisti italský matematik V. Voterra. Motivací k sestavení tohoto modelu byla skutečnost, že během omezení rybolovu za první světové války v úlovcích vzrostlo procento dravých ryb. Na tuto skutečnost upozornil Volterru jeho zeť, mořský biolog U. D’Ancona, který si uvedený jev nedokázal zdůvodnit. Dokonce čekal pravý opak: při omezení rybolovu D’Ancona očekával zvýšení procentuálního podílu druhů menších ryb, které jsou potravou pro dravce. Volterrův model toto chování vysvětluje jako důsledek jednoduché představy interakce mezi dravými rybami a kořistí. Část modelu věnovaná populaci kořisti obsahuje předpoklad, že tato populace přirozeně roste, ale růst je zpomalen působením dravců. Více dravců vede k vyššímu zpomalení růstu kořisti. Příliš mnoho dravců může vést dokonce k negativnímu růstu, kdy populace kořisti vymírá. Část modelu věnovaná populaci dravců obsahuje předpoklad, že bez přítomnosti kořisti populace vymírá, ale čím více kořisti mají dravci k dispozici, tím spíše se toto vymírání převrátí v nárůst populace.
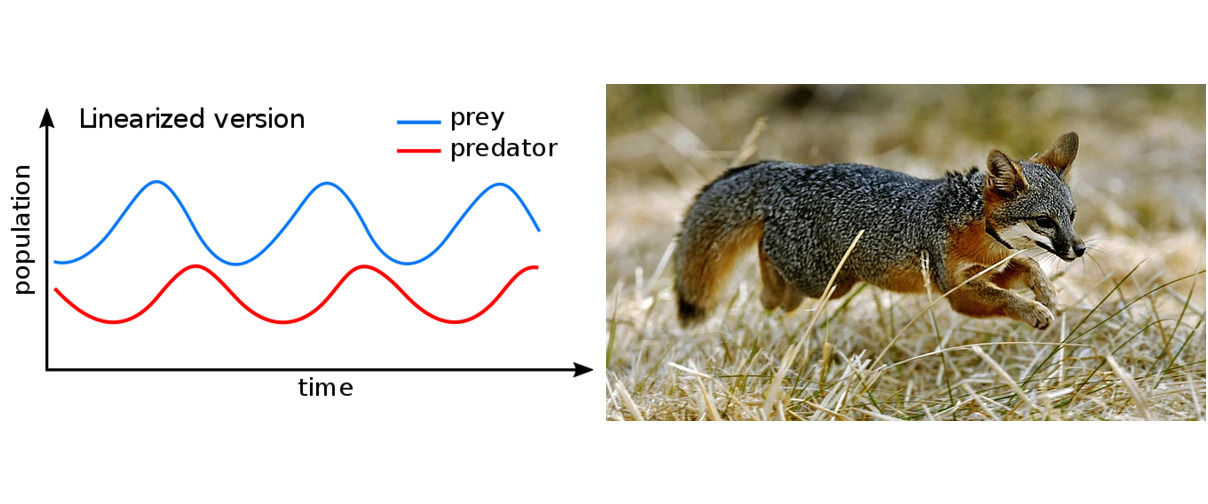
V systému popsaném výše přirozeně vznikají cykly. Dostatek kořisti umožní nárůst populace dravců. Mnoho dravců poté působí na populaci kořisti negativně do té míry, že populace kořisti začne vymírat. Toto vymírání má za následek nedostatek potravy pro dravce a ti začnou také vymírat. Po čase je populace dravce redukována natolik, že kořist přítomnost dravce pociťuje málo. Proto může její populace zase růst a namnožit se do původního stavu. To však opět umožní růst populace dravce a uzavírá se cyklus. Velmi pěkně jsou periodické změny velikosti obou populací patrné ze záznamů výkupu kožešin sněžného zajíce a rysa v oblasti Hudsonova zálivu.
Volerra svým modelem vysvětlil nejenom vznik cyklů. Vysvětlil i to, že omezením lovu se rovnovážná poloha, okolo které populace dravce a kořisti oscilují, posune ve prospěch dravce a nikoliv kořisti. Tento jev, kterého si všiml D’Ancona, se nazývá Volterrův efekt.
Stejný model jako Volterra navrhl již v roce 1910 americký matematik A. Lotka a proto se model dnes nazývá Lotkův–Volerrův model.

Podobné periodické výkyvy jako v Lotkově–Volterrově modelu je možné pozorovat i v kanadských lesích. Zde přibližně po 30 až 40 letech docházelo k masovému přemnožení obaleče smrkového (Choristoneura fumiferana). Populace tohoto motýla je relativně malá, ale některé roky zvýší tisícinásobně a jeho housenky dokáží zahubit 80% stromů v lese a les prakticky zničit. Jeden z posledních masových výskytů byl od roku 2006 v Quebecu. Zde do roku 2019 bylo zasaženo cca 9.6 milionu hektarů (zdroj https://www.nrcan.gc.ca), což je více než rozloha Maďarska.
V roce 1978 navrhli vědci D. Ludwig, D. Jones a C Holling model, který dokázal nejenom modelovat vývoj populace obaleče, ale pomohl objasnit i důvody, proč k popisovanému přemnožení dochází. Důvodem byla predace. V tomto případě šlo o konzumaci housenek obaleče ptáky. Ptáci sloužili v přírodě jako faktor omezující počty housenek, ovšem jenom do jistého limitu. Když se les dostatečně rozrostl, poskytl dostatek potravy i populaci housenek. Populace housenek se rozrostla a to do takové míry, že ptáci dosáhli při konzumaci potravy své saturace a nedokázali dál stavy housenek redukovat. Tím se role ptáků jako predátorů stala méně významnou a populace housenek se mohla velmi rychle množit a poté zdevastovat les.
V tomto případě je predace důležitá pro omezení populace housenek. Protože ptáci jako predátoři mají mnohem pomalejší cyklus rozmnožování než obaleč, je možné jejich populaci považovat za konstantní. Díky saturaci poté ptáci dokáží omezit rychlost růstu obaleče jen do omezené míry. Toto omezení však od určité velikosti populace přestává stačit a dojde k nekontrolovatelnému přemnožení.
Liška ostrovní (Urocyon littoralis) je jedinečný živočišný druh, endemit žijící jenom na ostrůvcích okolo Kalifornie. Je velká jako kočka a díky absenci přirozených nepřátel důvěřivá. Jako druh je citlivá a zranitelná vlivem malé genetické variability a malé odolnosti vůči nemocem zavlečeným z pevniny. Je to jedna z nejmenších psovitých šelem. Na rozdíl od ostatních psovitých šelem umí šplhat po stromech.
Vlivem činnosti člověka se populace lišky ostrovní dostala na přelomu tisíciletí do velkých potíží. Na ostrově San Miguel klesla populace z 450 dospělých jedinců v roce 1994 na 15 v roce 1999 (viz https://www.iucnredlist.org/species/22781/13985603). Podobná situace byla i na okolních ostrovech, z nichž každý je osídlen samostatným poddruhem lišky ostrovní. Příčinou úhynu byl celý řetězec událostí: produkce insekticidu DDT ve 40. letech 20. století měla za následek vymření orla bělohlavého (Haliaeetus leucocephalus) a ten byl nahrazen orlem skalním (Aquila chrysaetos). Predátora živícího se rybami tímto na ostrově vystřídal predátor preferující savce. Toto bylo pro lišky ostrovní fatální. Lišky, dříve vrcholoví predátoři, se staly najednou kořistí a na přelomu tisíciletí se ocitly těsně před vyhubením. A na rozdíl od Lotkova–Volterrova modelu nebylo možné doufat v návrat lišek na původní stavy díky oscilacím, protože orli měli i alternativní potravu v podobě divokých prasat a skunků.
Naštěstí se nesmírným úsilím podařilo lišky ostrovní jako druh zachránit. Nejprve se podařilo správně identifikovat příčiny jejich úbytku. Poté již stačilo populaci lišek opětovně rozmnožit a zajistit podmínky, ve kterých je populace stabilní. To zahrnovalo vybití divokých prasat, přesídlení orlů skalních, návrat orlů bělohlavých, umělé rozmnožení lišek, jejich návrat do přírody a jejich vakcinaci proti zavlečeným chorobám. To vše se podařilo v rekordním čase, za jednu dekádu. Jednalo se o jeden z nejúspěšnějších záchranných programů pro savce.
Důležitou komponentou modelu dravce a kořisti, ať se jedná o kterýkoliv z výše uvedených případů, je trofická funkce. Tato funkce modeluje působení jednoho predátora na populaci kořisti. Udává rychlost, s jakou zpomaluje růst kořisti jeden dravec. Je-li \(x\) velikost populace kořisti a \(y\) rychlost, s jakou jeden dravec zpomaluje růst kořisti (tj. množství kořisti ulovené dravcem za jednotku času), můžeme tuto funkci matematicky zapsat ve tvaru \[y=f(x).\] Budeme se snažit najít přirozené předpoklady, které trofická funkce musí splňovat. Poté se pro ni pokusíme najít vhodný analytický tvar.
Úloha 1. Předpoklady o působení dravce na kořisti mají odraz ve vlastnostech, které musí trofická funkce mít. Převeďte následující požadavky do terminologie popisu vlastností matematických funkcí.
Vyjádřete tyto vlastnosti pomocí pojmů, které používáme pro popis vlastností funkcí. Jaké vlastnosti funkcí odpovídá každý z uvedených bodů?
Řešení.
Část 1) Funkce \(y=f(x)\) je rostoucí.
Část 2) Funkce \(y=f(x)\) prochází počátkem, tj. platí \(f(0)=0\).
Část 3) Funkce \(y=f(x)\) je shora ohraničená, její graf má v nekonečnu vodorovnou asymptotu.
Trofická funkce udává, kolik kořisti zahubí jeden dravec za jednotku času při dané velikosti populace kořisti. Musí tedy být definována na množině nezáporných čísel a funkční hodnoty budou nezáporné. V předchozí části bylo ukázáno, že trofická funkce má procházet počátkem a růst k vodorovné asymptotě (růst a ohraničenost shora). Tyto vlastnosti nebudou splněny, pokud budeme hledat trofickou funkci mezi lineárními funkcemi. Zkusíme tedy nejjednodušší nelineární funkci, nepřímou úměrnost.
Úloha 2. Vyjděte z grafu funkce \(y=\frac 1x\). Na této funkci provádějte transformace, které mění graf způsobem popsaným níže.
Řešení. Funkce, jejíž graf vznikne rozšířením grafu funkce \(y=\frac{1}{x}\) ve svislém směru \(k\)-krát je \[y=\frac{k}{x}.\] Převrácení a posun dosáhneme vynásobením funkce fakorem \(-1\) a přičtením hodnoty \(S\). Tím dostáváme funkci \[y=S-\frac{k}{x}.\] Posun doprava o \(b\) zajistíme substitucí výrazu \(x+b\) za \(x\). Tím dostáváme funkci \[y=S-\frac {k}{x+b}.\] Po převedení na společného jmenovatele má funkce tvar \[y=\frac{Sx+Sb}{x+b}-\frac{k}{x+b}=\frac{Sx + (Sb-k)}{x+b}.\] Má-li platit \(f(0)=0,\) musí být splněna podmínka \[Sb-k=0.\] Tato podmínka ukazuje, že tři konstanty nejsou nezávislé, ale je mezi nimi uvedená vazba.
Poznámka. V předchozí úloze jsme odvodili analytický tvar pro jednu ze základních trofických funkcí. Jedná se o rostoucí funkci, která z počátku roste směrem k vodorovné asymptotě a rychlost růstu postupně klesá. Taková funkce se nazývá Hollingova funkce II typu. Bývá obvyklé ji psát ve tvaru \[f(x)=\frac {Sx}{x+b},\tag{1}\] kde \(S\) je hladina saturace a \(b\) konstanta, jejíž význam objasníme v následující úloze.
Úloha 3. Ukažte, že pro velikost populace rovnu \(b\) je hodnota trofické funkce (1) rovna polovině hodnoty saturace.
Řešení. Přímým dosazením do (1) dostáváme \[f(b)=\frac{Sb}{b+b}=\frac {Sb}{2b}=\frac S2.\] Tím je tvrzení dokázáno.
Následující úkol ukazuje opačný proces, kdy z trofické funkce ve tvaru (1) odvodíme tvar ukazující postupné transformace funkce \(y=\frac 1x\).
Úloha 4. Převeďte funkci \[y=\frac {6x}{x+2}\] do tvaru udávajícího postupné transformace funkce \(y=\frac 1x\) na graf zadané funkce.
Řešení. Úlohu vyřešíme tak, že v čitateli vytvoříme násobek jmenovatele a rozdělíme zlomky.
\[\frac {6x}{x+2} = \frac {6(x+2)-12}{x+2}=\frac {6(x+2)}{x+2}-\frac {12}{x+2}=6-12\frac 1{x+2}\]
Tento výpočet ukazuje, že graf uvedené funkce obdržíme rozšířením grafu funkce ve svislém směru dvanáctkrát, převrácením okolo vodorovné osy, posunutím o šest jednotek nahoru a dvě jednotku doleva.
Úloha 5. Trofická funkce je dána vztahem \[y=\frac{3x}{x+5}.\] Převeďte tento výraz na tvar, z kterého vidíme transformace, které je nutno udělat na grafu funkce \(y=\frac {1}{x}\), abychom dostali graf zadané funkce.
Úloha 6. Trofická funkce je dána vztahem \[y=\frac{4x}{x+8}.\] Převeďte tento výraz na tvar, z kterého vidíme transformace, které je nutno udělat na grafu funkce \(y=\frac {1}{x}\), abychom dostali graf zadané funkce.
Úloha 7. Sestavte trofickou funkci, pokud víte, že rychlost konzumace potravy při saturaci predátorů je \(6\) a že konzumace probíhá poloviční rychlostí pro populaci kořisti o velikosti \(210\).