Popis vývoja HDP
 25 min.,
25 min.,  1/3
1/3 Hrubý domáci produkt (HDP, v angličtine GDP) je peňažným vyjadrením celkovej hodnoty tovarov a služieb novo vytvorených v danom období na určitom území. V makroekonomike sa HDP používa ako ukazovateľ pre určovanie výkonnosti ekonomiky štátov. Môžeme ho teda použiť napríklad pre porovnanie výkonnosti jednotlivých štátov Európskej únie v roku 2023 (viz. Obrázok 1).
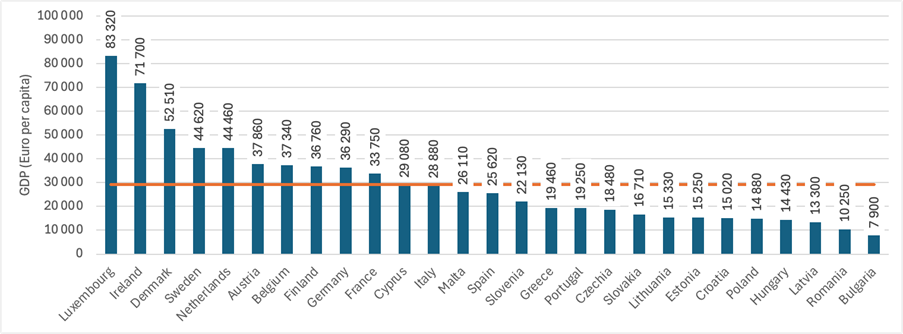
Ďalším využitím je sledovanie výkonnosti štátov v priebehu času. Pozrime sa teraz napríklad na to, ako sa vyvíjalo HDP Európskej únie prepočítané na osobu v rokoch 2020 až 2023, keď Európska únia mala 27 členských štátov. Časovú radu, ktorá tento vývoj dokladá, vidíme na Obrázku 2.
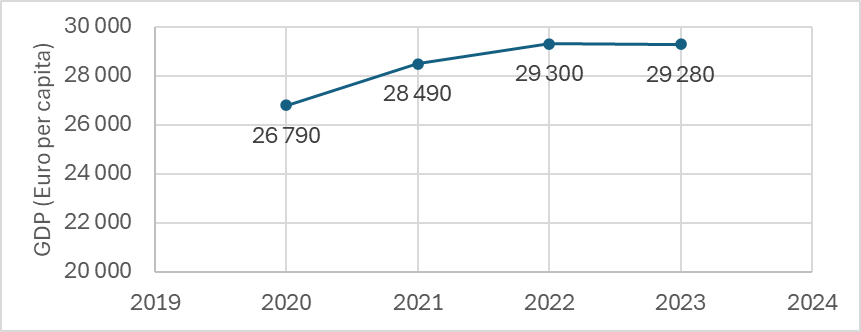
Časová rada, ktorú vývoj HDP predstavuje, je tzv. intervalová časová rada, t. j. časová rada, ktorej údaje závisia od dĺžky intervalu, ktorý je sledovaný (v tomto prípade od dĺžky daného roku). Nech časovým okamihom \(t_1,\,t_2,\,\ldots\,t_n\) zodpovedajú hodnoty časovej rady \(y_1,\,y_2,\,\ldots\,y_n\).
Základnou charakteristikou, ktorú na popis tejto časovej rady používame, je jej priemer.
Priemer intervalovej časovej rady (\(\bar{y}\)) vypočítame aritmetický priemer \[
\bar{y} = \frac{y_1 + y_2 + \dots + y_n}{n}. \tag{1}
\]
Okrem priemeru nás mnohokrát zaujímajú základné miery dynamiky časových radov, ktoré umožňujú charakterizovať základné rysy ich „správania".
Absolútne prírastky (\(\Delta y_t\)) sú najjednoduchšou mierou dynamiky. Hovoria nám „o koľko" sa zmenila časová rada medzi jednotlivými okamihmi. \[ \Delta y_t = y_t - y_{t-1}, \quad t = 2,\,3, \,\dots,\, n.\tag{2} \]
Priemerný absolútny prírastok (\(\bar{\Delta}\)) udává „o koľko" sa priemerne zmenila časová rada za obdobie medzi dvoma meraniami počas sledovaného obdobia.
Súčet absolútnych prírastkov vyjadruje celkovú zmenu časovej rady za sledované obdobie („o koľko" sa zmenila časová rada medzi časmi t1t_1 \(t_1\) a \(t_n\)): \[ \Delta y_2 + \Delta y_3 + \dots + \Delta y_n = (y_2 - y_1) + (y_3 - y_2) + \dots + (y_n - y_{n-1}) = y_n - y_1. \]
Priemerný absolútny prírastok preto určíme ako aritmetický priemer absolútnych prírastkov:
\[ \bar{\Delta} = \frac{\Delta y_2 + \Delta y_3 + \dots + \Delta y_n}{n-1} = \frac{y_n - y_1}{n-1}.\tag{3} \]
Všimnime si, že na výpočet stačí poznať počiatočnú hodnotu \(y_1\), koncovú hodnotu \(y_n\) a počet hodnôt \(n\).
Koeficienty rastu (tempá rastu, \(k_t\)) sú ďalšou mierou dynamiky časových radov. Udávajú „koľkonásobne" sa zmenila časová rada medzi jednotlivými časovými okamihmi
\[ k_t = \frac{y_t}{y_{t-1}}, \quad t = 2,\,3,\, \dots,\, n.\tag{4} \]
Priemerný koeficient rastu (\(\bar{k}\)) nám hovorí „koľkonásobne" sa priemerne zmenila časová rada medzi dvoma meraniami počas sledovaného obdobia.
V tomto prípade je celkový koeficient rastu („koľkonásobne" sa zmenila časová rada medzi časmi \(t_1\) a \(t_n\)) nie súčtom, ale súčinom jednotlivých koeficientov rastu \[ k_2 \cdot k_3 \cdot \ldots \cdot k_n = \frac{y_2}{y_1} \cdot \frac{y_3}{y_2} \cdot \ldots \cdot \frac{y_n}{y_{n-1}} = \frac{y_n}{y_1}. \] Priemerný koeficient rastu teda určíme ako geometrický priemer jednotlivých koeficientov rastu \[ \bar{k} =\sqrt[n-1]{k_2 \cdot k_3 \cdot \ldots \cdot k_n} =\sqrt[n-1]{\frac{y_n}{y_1}}.\tag{5} \]
Podobne ako pri výpočte priemerného absolútneho prírastku, aj v tomto prípade stačí na výpočet poznať počiatočnú hodnotu \(y_1\), koncovú hodnotu \(y_n\) a počet hodnôt \(n\).
Relatívne prírastky (\(\delta_t\)) použijeme, ak chceme vedieť „o koľko percent" sa zmenila časová rada medzi jednotlivými okamihmi. Relatívne prírastky ľahko určíme pomocou koeficientov rastu:
\[ \delta_t = \frac{\Delta y_t}{y_{t-1}} \cdot 100 = \frac{y_t - y_{t-1}}{y_{t-1}} \cdot 100 = \left(\frac{y_t}{y_{t-1}} - 1\right) \cdot 100 = (k_t - 1) \cdot 100, \quad t = 2,\,3,\, \dots,\, n. \tag{6} \]
Stačí si uvedomiť, že napríklad cena výrobkov vzrástla na \(1{,}5\), čo znamená nárast o \(50\% \,(=(1{,}5-1)\cdot100\%)\).
Priemerný relatívny prírastok (\(\bar{\delta}\)) udává, o koľko percent sa priemerne zmenila časová rada za obdobie medzi dvoma meraniami počas sledovaného obdobia. Vypočítame ho pomocou priemerného koeficientu rastu: \[ \bar{\delta} = (\bar{k} - 1) \cdot 100.\tag{7} \]
Poznámka. Súčet (súčin) jednotlivých relatívnych prírastkov nie je rovný celkovému relatívnemu prírastku („o koľko percent" sa zmenila časová rada medzi časmi \(t_1\) a \(t_n\)), preto na výpočet priemerného relatívneho prírastku nemožno použiť aritmetický ani geometrický priemer jednotlivých relatívnych prírastkov.
Teraz sa pokúsime o základný popis časovej rady prezentujúcej vývoj HDP (v eurách na osobu), ktorú nájdeme na obrázku 2.
Úloha 1. Určte priemerné ročné HDP (v eurách na osobu) Európskej únie v rokoch 2020 až 2023.
Riešenie. JAko bolo uvedené vo vzťahu (1), priemerné ročné HDP určíme ako prostý aritmetický priemer analyzovanej časovej rady
\[ \bar{y} = \frac{y_1 + y_2 + y_3 + y_4}{4} = \frac{26\,790 + 28\,490 + 29\,300 + 29\,280}{4} \approx 28\,465. \]
V rokoch 2020-2023 bolo priemerné ročné HDP Európskej únie \(28\,465\) eur na osobu.
Úloha 2. Určte medziročné prírastky HDP (v eurách na osobu) Európskej únie v rokoch 2020 až 2023 a zodpovedajúci priemerný medziročný prírastok HDP za toto obdobie.
Riešenie. Medziročné prírastky HDP nám hovoria „o koľko" sa medziročne zmenilo HDP. Určíme ich preto ako absolútne prírastky podľa vzťahu (2) a zapíšeme do tabuľky.
| rok | HDP (euro/osoba) | Medziročné prírastky HDP (euro/osoba) |
|---|---|---|
| 2020 | \(26\,790\) | — |
| 2021 | \(28\,490\) | \(28\,490 - 26\,790 = 1\,700\) |
| 2022 | \(29\,300\) | \(29\,300 - 28\,490 = 810\) |
| 2023 | \(29\,280\) | \(29\,280 - 29\,300 = -20\) |
| priemer | \(28\,465\) | \(830\) |
- V roku 2021 vzrástlo medziročne v krajinách Európskej únie HDP o \(1\,700\) eur na osobu.
- V roku 2022 bol medziročný nárast HDP \(810\) eur na osobu.
- V roku 2023 došlo k medziročnému poklesu HDP o \(20\) eur na osobu.
Priemerný medziročný prírastok teraz môžeme podľa vzťahu (3) určiť ako aritmetický priemer medziročných prírastkov alebo len pomocou počiatočnej a koncovej hodnoty analyzovanej časovej rady:
\[
\bar{\Delta} = \frac{\Delta y_2 + \Delta y_3 + \Delta y_4}{4-1} = \frac{1\,700 + 810 + (-20)}{3} = 830
\] alebo
\[
\bar{\Delta} = \frac{y_4 - y_1}{4-1} = \frac{29\,280 - 26\,790}{3} = 830.
\]
V letech 2020 až 2023 rostlo v Evropské unii HDP ročně v průměru o \(830\) eur na osobu.
Úloha 3. Určte medziročné tempá rastu HDP Európskej únie v rokoch 2020 až 2023 a zodpovedajúce priemerné tempo rastu HDP za toto obdobie.
Riešenie. Medziročné tempá rastu HDP nám hovoria „koľkokrát" sa medziročne zmenilo HDP. Určíme ich preto ako koeficienty rastu podľa vzťahu (4), pre prehľadnosť ich opäť zapíšeme do tabuľky.
| rok | HDP (euro/osoba) | Medziročné prírastky HDP (euro/osoba) | Tempo rastu (-) |
|---|---|---|---|
| 2020 | \(26\,790\) | — | — |
| 2021 | \(28\,490\) | \(1\,700\) | \(\frac{28\,490}{26\,790} \approx 1{,}063\) |
| 2022 | \(29\,300\) | \(810\) | \(\frac{29\,300}{28\,490} \approx 1{,}028\) |
| 2023 | \(29\,280\) | \(-20\) | \(\frac{29\,280}{29\,300} \approx 0{,}999\) |
| priemer | \(28\,465\) | \(830\) | — |
- V roku 2021 vzrástlo HDP v krajinách Európskej únie medziročne cca \(1{,}063\) krát, t. j. vzrástlo medziročne cca o \(6{,}3\%\).
- V roku 2022 vzrástlo HDP v krajinách Európskej únie medziročne cca \(1{,}028\) krát, t. j. vzrástlo medziročne cca o \(2{,}8\%\).
- V roku 2023 vzrástlo HDP v krajinách Európskej únie medziročne cca \(0{,}999\) krát, t. j. došlo k medziročnému poklesu cca o \(0{,}1\%\).
Priemerné medziročné tempo rastu môžeme teraz podľa vzťahu (5) určiť ako buď ako geometrický priemer medziročných temp rastu, alebo len pomocou počiatočnej a koncovej hodnoty analyzovanej časovej rady:
\[ \bar{k} = \sqrt[n-1]{k_2 \cdot k_3 \cdot k_4} = \sqrt[3]{1{,}063 \cdot 1{,}028 \cdot 0{,}999} \approx 1{,}030 \]
alebo
\[ \bar{k} = \sqrt[n-1]{\frac{y_4}{y_1}} = \sqrt[3]{\frac{29\,280}{26\,790}} \approx 1{,}030 \]
V rokoch 2020 až 2023 bolo v Európskej únii priemerné medziročné tempo rastu HDP (eur na osobu) \(1{,}030\), t. j. HDP (eur na osobu) rástlo medziročne v priemere o \(3{,}0\%\).
Poznámka. Ak budeme počítať priemerné tempo rastu ako geometrický priemer jednotlivých koeficientov rastu uvedených v tabuľke pri riešení Úlohy 3, budeme pracovať so zaokrúhlenými údajmi a vnášať tak do výpočtu chybu s tým súvisiacu. Preto odporúčame na výpočet používať radšej len počiatočné a koncové hodnoty analyzovanej časovej rady.
Úloha 4. Určte medziročné relatívne prírastky HDP Európskej únie v rokoch 2020 až 2023 a zodpovedajúci priemerný relatívny prírastok HDP za toto obdobie.
Riešenie. Túto úlohu sme už vyriešili v rámci interpretácie temp rastu zistených v úlohe 3. Ak hovoríme, že v roku 2021 vzrástlo HDP medziročne \(1{,}063\) krát, je to to isté, ako keď budeme tvrdiť, že v roku 2021 vzrástlo HDP medziročne o \(6{,}3\%\).
To tvrdia aj vzťahy (6) a (7), ktoré uvádzajú, ako súvisí relatívny prírastok v percentách (resp. priemerný relatívny prírastok v percentách) a tempo rastu (resp. priemerné tempo rastu).
Výsledky sú uvedené v nasledujúcej tabuľke.
| rok | HDP (euro/osoba) | Medziročné prírastky HDP (euro/osoba) | Tempo rastu (-) | Relatívny prírastok (%) |
|---|---|---|---|---|
| 2020 | \(26\,790\) | — | — | — |
| 2021 | \(28\,490\) | \(1\,700\) | \(1{,}063\) | \(6{,}3\) |
| 2022 | \(29\,300\) | \(810\) | \(1{,}028\) | \(2{,}8\) |
| 2023 | \(29\,280\) | \(-20\) | \(0{,}999\) | \(-0{,}1\) |
| priemer | \(28\,465\) | \(830\) | \(1{,}030\) | \(3{,}0\) |
Literatúra
Hrubý domácí produkt (HDP) - Metodika. Online. Český statistický úřad. 2024. Dostupné z: https://csu.gov.cz/hruby_domaci_produkt_-hdp-. [cit. 2024-12-18].
Real GDP per capita. Online. Eurostat. 2024. Dostupné z: https://ec.europa.eu/eurostat/databrowser/view/sdg_08_10/default/table. [cit. 2024-12-18].