Pyramidové schéma
 25 min.,
25 min.,  2/3
2/3 Představte si, že vám někdo ve jménu investiční společnosti nabídne rychlé zhodnocení vašich peněz a jediné, co pro to budete muset udělat, je přesvědčit k investicím další tři kamarády. Vaše peníze však ve skutečnosti nebudou využity ke koupi zlata nebo akcií, ale rozdělí si je mezi sebou lidé, kteří se upsali společnosti před vámi. Pokud se vám podaří nějaké tři kamarády přesvědčit, dostanete z jejich peněz podíl a stejně tak z dalších lidí, které přesvědčí oni – dokud celý model nezkrachuje na nedostatek nových investorů a majitel společnosti záhadně neodletí na Bahamy. Nutno říct, že taková věc kamarádským vztahům obecně neprospívá.
Právě jste naletěli na jeden z nejrozšířenějších podvodných obchodních modelů – pyramidové schéma.
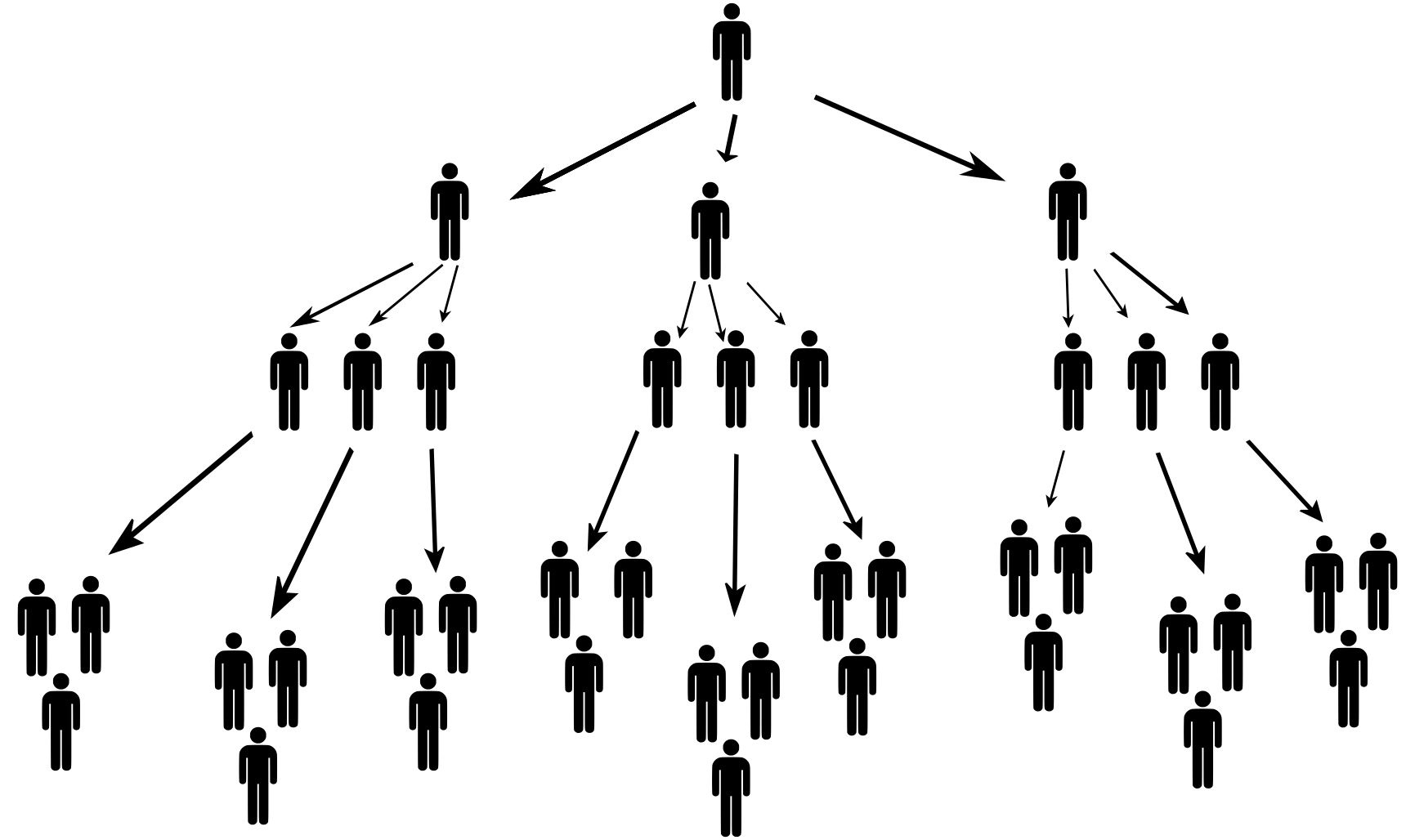
Zadání
Zakladatel společnosti (první úroveň pyramidy) sežene tři investory (druhá úroveň pyramidy) a od každého vybere fixní vstupní poplatek \(20\,000\,\text{Kč}\). Úkolem každého z tří investorů je přivést do schématu další tři nové investory (třetí úroveň pyramidy) a vybrat od každého opět vstupní poplatek \(20\,000\,\text{Kč}\). Totéž se opakuje pro další úrovně. Pro jednoduchost budeme předpokládat, že nabírání nových členů nastane vždy až po zaplnění celé úrovně pyramidy – tedy např. nabírání členů do čtvrté úrovně začíná až po nabrání všech devíti investorů ve třetí úrovni.
Vstupní poplatek nově příchozích členů se distribuuje mezi stávající účastníky následovně: \(6\,000\,\text{Kč}\) dostane člověk A, který nového člena přivedl, \(1\,000\,\text{Kč}\) dostane člověk B, který přivedl člověka A, dalších \(1\,000\,\text{Kč}\) dostane člověk C, který přivedl člověka B, dalších \(1\,000\,\text{Kč}\) dostane člověk D, který přivedl člověka C, a dále, dokud není vstupní poplatek rozdělen. Jestliže dojde k výplatě peněz zakladateli společnosti, dostává zbytek poplatku.
Úloha 1. Kdy se nově příchozímu člověku vrátí peníze ze vstupního poplatku?
Řešení. Nově příchozí člověk zaplatí vstupní poplatek \(20\,000\,\text{Kč}\). Aby se mu peníze vrátily, musí nabrat tři nové členy (od nich inkasuje celkem \(18\,000\,\text{Kč}\)) a ti dále musí nabrat alespoň dva další členy (od kterých dostane zbylých \(2\,000\,\text{Kč}\)).
Úloha 2. Při dosažení určité úrovně pyramidy dojde poprvé k tomu, že zakladatel společnosti nedostane ze vstupních poplatků nových členů žádné peníze.
- Která úroveň to je?
- Kolik lidí je v celé pyramidě po naplnění této úrovně? Srovnejte tento počet s počtem lidí ve vaší škole nebo obci.
- Určete procentuální podíl lidí, kteří jsou po naplnění této úrovně ve ztrátě.
Řešení.
Řešení části 2.1. Jestliže ze vstupního poplatku nově příchozího člena zakladatel společnosti poprvé žádné peníze nedostane, znamená to, že se nad tímto členem nachází 16 úrovní (\(6\,000\,\text{Kč}\) dostane člověk v úrovni výše, \(14\cdot 1\,000\,\text{Kč}\) dostanou lidé v čtrnácti vyšších úrovních a zakladatel v první úrovni nedostane nic). Nově příchozí člen se tak nachází v 17. úrovni.
Řešení části 2.2. Počty lidí v jednotlivých úrovních tvoří geometrickou posloupnost s prvním členem \(a_1=1\) a kvocientem \(q=3\). Počet lidí v pyramidě o sedmnácti úrovních je pak součtem prvních sedmnácti členů této posloupnosti: \[s_{n}=a_1\cdot\frac{q^n-1}{q-1},\qquad s_{17}=1\cdot\frac{3^{17}-1}{3-1}=64\,570\,081.\] Je vidět, že by do schématu musela být zapojena celá populace většího státu (přibližně odpovídá populaci Francie).
Řešení části 2.3. Z první úlohy vyplývá, že ztrátovou část pyramidy tvoří poslední dvě úrovně. Počet lidí ve ztrátě tak odpovídá součtu šestnáctého a sedmnáctého členu zmiňované geometrické posloupnosti:
\[ a_{16}+a_{17}=3^{15}+3^{16}=57\,395\,628. \]
Nyní můžeme určit procentuální podíl lidí ve ztrátě: \[P=100\cdot\frac{57\,395\,628}{64\,570\,081}\,\%\doteq 88{,}89\,\%.\]
Úloha 3. Reálně se v případech z ČR pohyboval počet účastníků v řádech jednotek tisíců. Řekněme proto, že je počet účastníků v naší pyramidě po naplnění určité úrovně v rozmezí \(2\,000\,–\,8\,000\).
- Která úroveň to je?
- Určete procentuální podíl lidí, kteří jsou nyní ve ztrátě.
- Určete celkový zisk zakladatele společnosti.
- Určete celkový zisk investora ve druhé úrovni pyramidy.
- Kolik procent ze všech vybraných vstupních poplatků bude vyplaceno lidem v prvních třech úrovních pyramidy?
Řešení.
Řešení části 3.1. Úlohu lze řešit postupným dosazováním přirozených čísel do vzorce pro součet prvních \(n\) členů geometrické posloupnosti. Uvedeme zde však řešení užitím exponenciální nerovnice. Musí platit \(2\,000 \leq s_n \leq 8\,000\), tedy po dosazení do vzorce (\(a_1=1\), \(q=3\)) dostáváme:
\[ 2\,000 \leq \dfrac{3^n-1}{2} \leq 8\,000 \]
\[ 4\,001 \leq 3^n \leq 16\,001 \]
\[ \log_3 4\,001 \leq n \leq \log_3 16\,001. \]
Protože \(\log_3 4\,001 \doteq 7{,}55\) a \(\log_3 16\,001 \doteq 8{,}81\), má nyní pyramida osm úrovní (dosazením do \(s_8\) se můžeme přesvědčit, že počet lidí v pyramidě je nyní \(3\,280\)).
Řešení části 3.2. Ztrátovou část pyramidy opět tvoří poslední dvě úrovně. Obdobně jako v úloze 2.3 je počet lidí ve ztrátě roven \(a_7+a_8=3^6+3^7=2\ 916\). Stanovíme procentuální podíl: \[ P'=100\cdot\frac{2\,916}{3\,280}\,\%\doteq 88{,}90\,\%. \] Můžeme si všimnout, že se výsledek příliš neliší od výsledku úlohy 2.3, i když jsou počty uvažovaných lidí řádově odlišné.
Řešení části 3.3. Zakladatel společnosti dostane od každého člověka v druhé úrovni celý vstupní poplatek (\(20\,000\,\text{Kč}\)), od každého člověka v třetí úrovni \(14\,000\,\text{Kč}\), od každého člověka v čtvrté úrovni \(13\,000\,\text{Kč}\) atd. Protože má pyramida nyní osm úrovní, celkový zisk zakladatele \(Z_1\) spočteme \[Z_1=3\cdot 20\,000 + 3^2\cdot 14\,000 + 3^3\cdot 13\ 000 + \cdots + 3^7\cdot 9\,000 = 31\,155\,000\,\text{Kč}.\]
Řešení části 3.4. Pro názornost ilustrujeme situaci investora na druhé úrovni obrázkem. Červeně zbarvený investor ve druhé úrovni pyramidy dostane od každého ze tří modře zbarvených investorů ve třetí úrovni \(6\,000\,\text{Kč}\). Tito tři investoři dále nabrali další lidi do schématu a od každého zeleně zbarveného člověka inkasuje červený investor \(1\,000\,\text{Kč}\). Podobně inkasuje i \(1\,000\,\text{Kč}\) od lidí nabraných zelenými investory a všech dalších lidí v “jeho” větvi pyramidy.
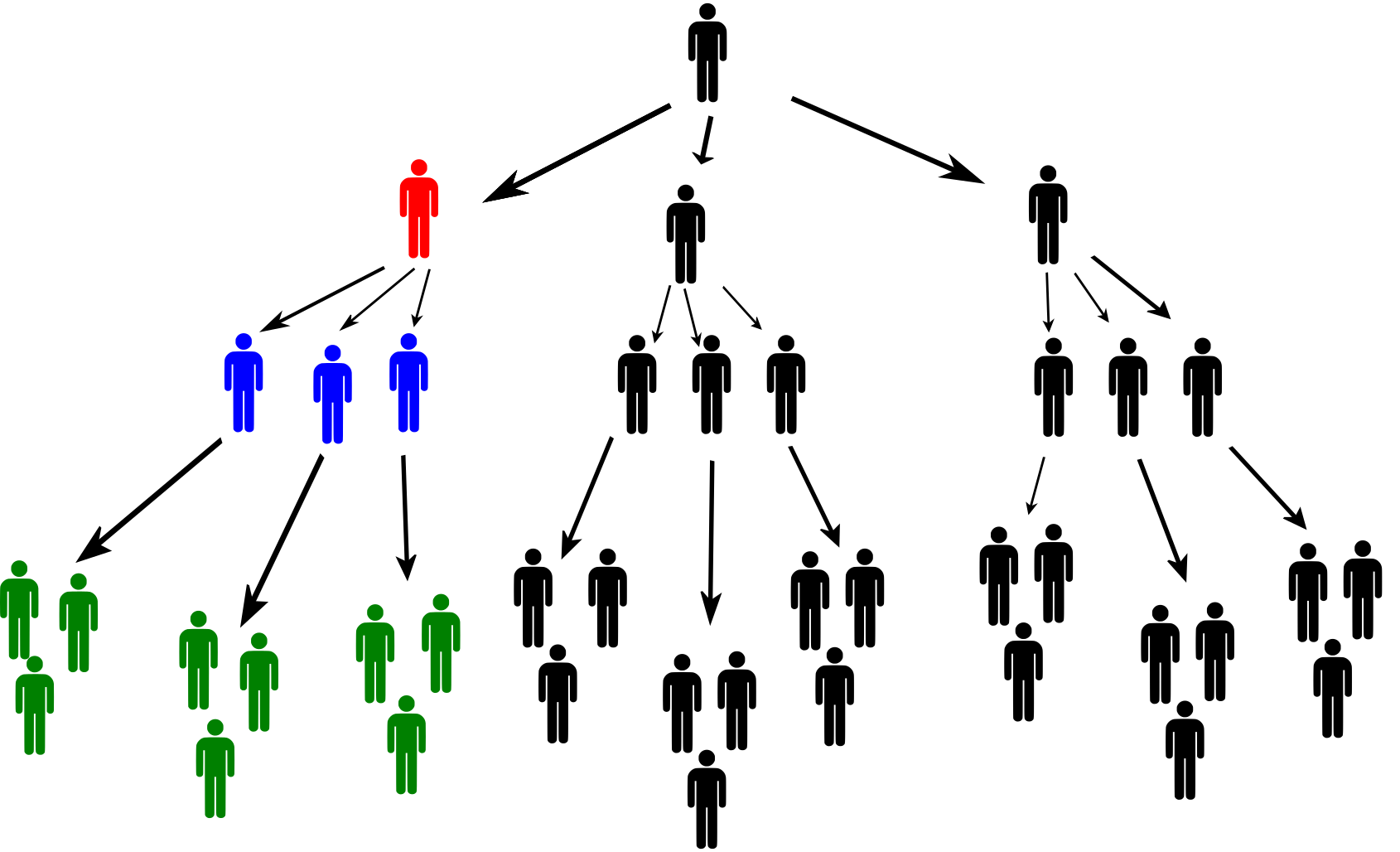
Určeme nyní zisk \(Z_2\) červeného investora. Počet lidí, od kterých dostane \(1\,000\,\text{Kč}\) je roven součtu \[3^2 + 3^3 + 3^4 + 3^5 + 3^6\] (celá pyramida má mít osm úrovní). Nesmíme dále zapomenout na odečtení vstupního poplatku. Tedy \[Z_2=3\cdot 6\,000 + (3^2+3^3 + 3^4 + 3^5 + 3^6 )\cdot 1\,000 - 20\,000\,\text{Kč} = 1\,087\,000\,\text{Kč}.\]
Řešení části 3.5. Z části 3.1 víme, že lidí v pyramidě je celkem \(3\,280\), každý až na zakladatele zaplatil na vstupních poplatcích \(20\,000\,\text{Kč}\). Celková suma vybraných peněz je proto \(65\,580\,000\,\text{Kč}\). Z částí 3.3 a 3.4 známe zisk zakladatele a investora ve druhé úrovni, spočítáme proto ještě zisk investora ve třetí úrovni (obdobně jako v části 3.4): \[Z_3=3\cdot 6\,000 + (3^2+3^3 + 3^4 + 3^5)\cdot 1\,000 - 20\,000 = 358\,000\,\text{Kč}.\] Nyní již můžeme stanovit podíl prostředků vyplacených lidem na prvních třech úrovních (\(S\) je celková suma): \[P''=100\cdot\frac{Z_1 + 3\cdot Z_2 + 9\cdot Z_3}{S}=100\cdot\frac{37\,638\,000}{65\,580\,000}\,\%\doteq 57{,}39\,\%.\] Pro lepší pochopení je důležité si uvědomit, že tento podíl z celkového “příjmu společnosti” je vyplacen pouze \(13\) lidem z \(3\,280.\) Přibližně \(0{,}4\,\%\) lidí v pyramidě tak dostane více než polovinu vybraných peněz. Není proto divu, že v řadě zemí světa je pyramidové schéma jako obchodní model zakázané (ČR mezi nimi bohužel dodnes, do roku 2023, není).
Literatura
Yates K. (2021). Matematika pro život. Praha: Kniha Zlín.
Illinois Attorney General. Pyramid schemes [online]. Dostupné z https://ag.state.il.us/consumers/pyramid.html [cit. 1. 6. 2023].