Esquema piramidal
 25 min.,
25 min.,  2/3
2/3 Imagina que alguien, en nombre de una sociedad de inversión, te ofrece una forma rápida de hacer crecer tu dinero. Lo único que tienes que hacer es convencer a tres de tus amigos para que inviertan también.
Sin embargo, tu dinero no se utilizará realmente para comprar oro o acciones, sino que se repartirá entre las personas que se hayan unido a la empresa antes que tú. Si consigues convencer a tres amigos para que se unan, obtendrás una parte de su dinero y también una porción de las otras personas a las que convenzan. Así hasta que todo el modelo se derrumba por falta de nuevos inversores y el propietario de la empresa vuela misteriosamente a las Bahamas. Hay que decir que este tipo de cosas no son buenas para las amistades.
Te has convertido en una víctima de uno de los modelos de negocio fraudulentos más extendidos – esquema piramidal.
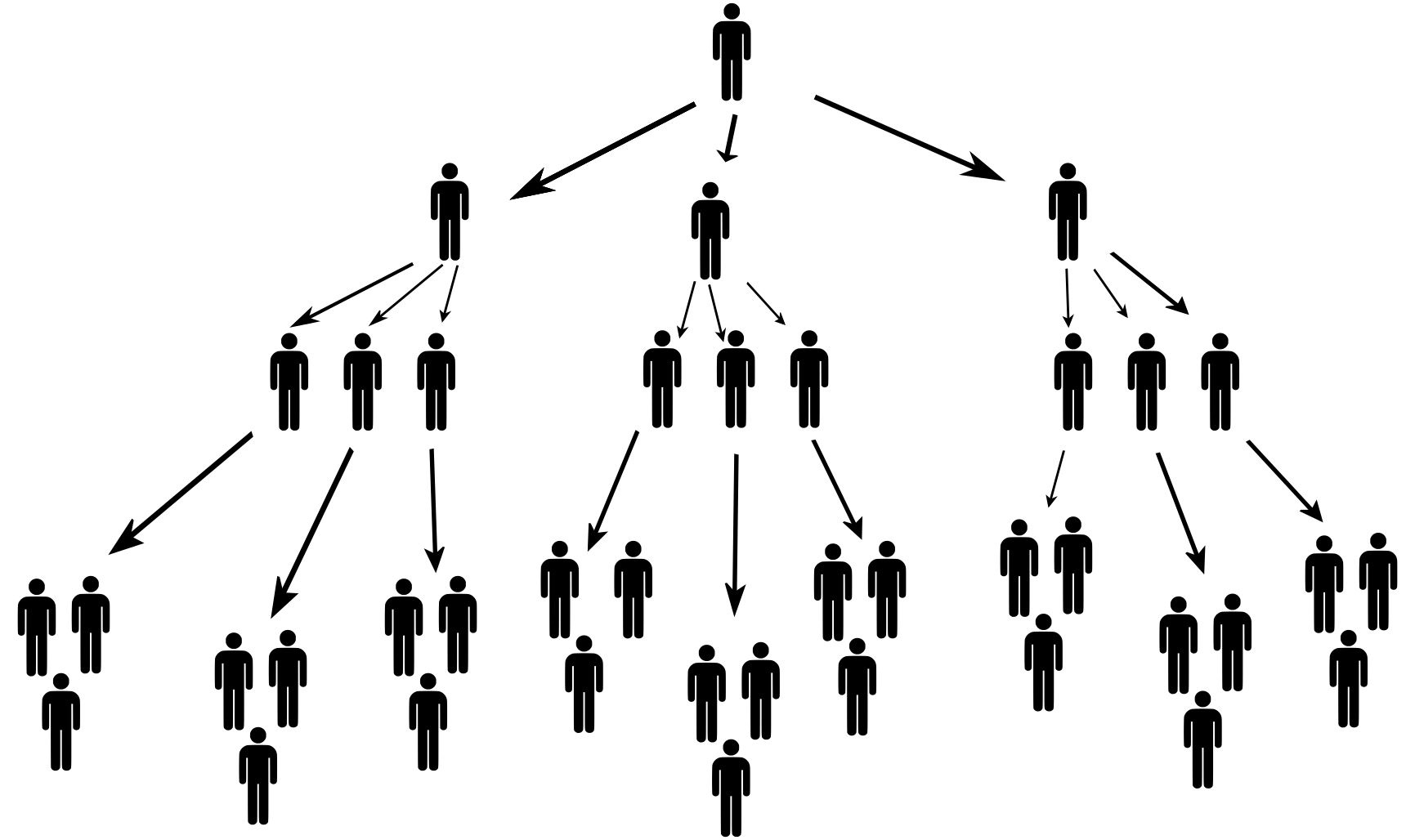
Tarea
El fundador de la empresa (el primer nivel de la pirámide) recluta a tres inversores (el segundo nivel de la pirámide) y cobra una cuota de entrada fija de 20 000 CZK a cada uno de ellos. La tarea de cada uno de los tres inversores consiste en incorporar tres nuevos inversores a la estafa (el tercer nivel de la pirámide) y cobrar una cuota de entrada de 20 000 CZK a cada uno de ellos. El mismo proceso se repite para los niveles siguientes. Para simplificar, supondremos que el reclutamiento de nuevos miembros se produce siempre después de que se haya llenado todo el nivel de la pirámide. Por ejemplo, el reclutamiento de nuevos miembros en el cuarto nivel sólo comienza después de reclutar a los nueve inversores del tercer nivel.
La cuota de inscripción abonada por los nuevos miembros se distribuye entre los participantes existentes del siguiente modo: 6 000 CZK para la persona A, que trajo a la nueva persona, 1.000 coronas checas a la persona B, que trajo a la persona A, y otra a la persona C, que trajo a la persona B. 1 000 CZK a la persona C, que trajo a la persona B, otra persona 1 000 CZK a la persona D, que trajo a la persona C, y así sucesivamente hasta dividir la cuota de inscripción. Si el dinero se paga al fundador de la empresa, éste se lleva el resto de la cuota.
Ejercicio 1. ¿Cuándo recibirá el recién llegado el reembolso de la cuota de afiliación?
Solución. Un recién llegado paga una cuota de inscripción de 20 000 CZK. Para recuperar el dinero, debe reclutar a tres nuevos miembros, de los que recibirá un total de 18 000 CZK. Además, cada uno de estos miembros reclutados debe traer al menos a dos miembros más, de los que el recién llegado recibirá las 2 000 CZK restantes.
Ejercicio 2. Cuando se alcanza un determinado nivel de la pirámide, el fundador de la empresa no recibe dinero de las cuotas de entrada por primera vez.
- ¿De qué nivel se trata?
- Después de alcanzar este nivel, ¿cuántas personas hay en toda la pirámide? Compara este número con el número de personas de tu escuela o comunidad.
- Calcula el porcentaje de personas que después de este nivel presentan pérdida.
La solución del ejercicio 2.
La solución del 2.1. Si el fundador de la empresa no recibe dinero de la cuota de ingreso del nuevo socio por primera vez, esto significa que hay 16 niveles por encima de ese socio (6.000 CZK van a la persona del nivel superior, \(14\cdot 1\ 000\) CZK a las personas de los 14 niveles superiores, y el fundador del primer nivel no recibe nada). Así pues, el nuevo afiliado se sitúa en el nivel 17.
La solución del 2.2. El número de personas en cada nivel forma una sucesión geométrica con el primer término \(a_1=1\) y el cociente \(q=3\). El número de personas en una pirámide de 17 niveles es entonces la suma de los 17 primeros términos de esta sucesión. \[s_{n}=a_1\cdot\frac{q^n-1}{q-1},\qquad s_{17}=1\cdot\frac{3^{17}-1}{3-1}=64\ 570\ 081\] Podemos observar que toda la población de un país más grande (aproximadamente equivalente a la población de Francia) tendría que participar en el plan.
La solución del 2.3. De la solución del primer ejercicio se deduce que la parte con pérdidas de la pirámide está formada por los dos últimos niveles. El número de personas que presentan pérdida es, por tanto, igual a la suma del decimosexto término y el decimoséptimo término de la sucesión geométrica: \(a_{16}+a_{17}=3^{15}+3^{16}=57\ 395\ 628\). Ahora podemos determinar el porcentaje de personas en la pérdida: \[P=100\cdot\frac{57\ 395\ 628}{64\ 570\ 081}\,\%\doteq 88{,}89\,\%.\]
Ejercicio 3. En casos reales de la República Checa, el número de participantes era del orden de unidades de miles. Por tanto, digamos que el número de participantes en nuestra pirámide se sitúa entre 2 000 y 8 000, tras alcanzar un determinado nivel.
- ¿De qué nivel se trata?
- Calcula el porcentaje de personas que ahora presentan pérdidas.
- Calcula el beneficio total del fundador de la empresa.
- Calcula el beneficio total del inversor en el segundo nivel de la pirámide.
- ¿Qué porcentaje de todas las tasas de inscripción recaudadas se pagará a las personas de los tres primeros niveles de la pirámide?
La solución del ejercicio 3.
La solución del 3.1. El problema se puede solucionar sustituyendo gradualmente los números naturales en la fórmula de la suma de los primeros \(n\) términos de la sucesión geométrica. Sin embargo, presentaremos una solución utilizando la inecuación exponencial. Se aplica que \(2\ 000 \leq s_n \leq 8\ 000\), por lo tanto después de sustituir en la fórmula (\(a_1=1\), \(q=3\)) obtenemos: \[2\ 000 \leq \dfrac{3^n-1}{2} \leq 8\ 000\] \[4\ 001 \leq 3^n \leq 16\ 001\] \[\log_3 4\ 001 \leq n \leq \log_3 16\ 001.\] Dado que \(\log_3 4\ 001 \doteq 7{,}55\) y \(\log_3 16\ 001 \doteq 8{,}81\), la pirámide tiene ahora ocho niveles (sustituyendo podemos ver que el número de personas en la pirámide es ahora de 3 280).
La solución del 3.2. De nuevo, las partes perdedoras de la pirámide son los dos últimos niveles. Al igual que en la solución 2.3, el número de personas que presentan pérdidas es igual a \(a_7+a_8=3^6+3^7=2\ 916\). Calculamos el porcentaje de participación: \[P'=100\cdot\frac{2\ 916}{3\ 280}\doteq 88{,}90\%.\] Podemos observar que el resultado no es muy diferente del resultado de 2.3, a pesar de que el número de personas consideradas difiere en varios órdenes.
La solución del 3.3. El fundador de la empresa percibe la totalidad de la tasa de inscripción de cada persona del segundo nivel (20 000 CZK), de cada persona en el tercer nivel 14 000 CZK, de cada persona en el cuarto nivel 13 000 CZK, etc. Como la pirámide tiene ahora ocho niveles, el beneficio total \(Z_1\) del fundador es
\[Z_1=3\cdot 20\ 000 + 3^2\cdot 14\ 000 + 3^3\cdot 13\ 000 + \cdots + 3^7\cdot 9\ 000 = 31\ 155\ 000\,\text{CZK}.\]
La solución del 3.4. Para aclarar la situación del inversor en el segundo nivel, mira la siguiente figura.
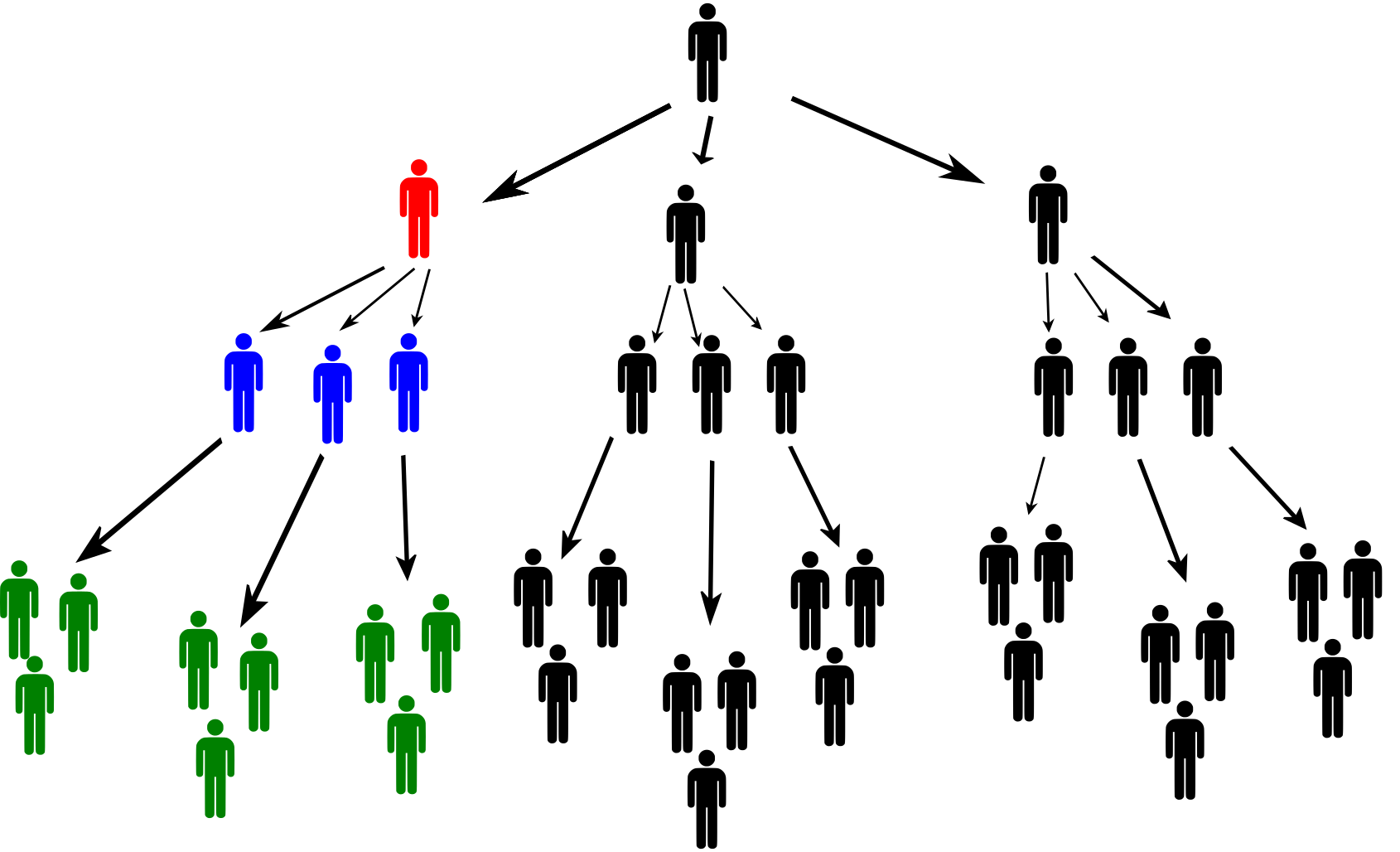
El inversor de color rojo del segundo nivel de la pirámide recibe 6 000 CZK de cada uno de los tres inversores de color azul del tercer nivel. A continuación, estos tres inversores reclutan a otras personas para la estafa. El inversor rojo recauda 1 000 CZK de cada inversor de color verde. Del mismo modo, cobra 1 000 CZK de las personas reclutadas por los inversores de color verde y de todas las demás personas de “su” rama de la pirámide.
Calculemos ahora el beneficio \(Z_2\) del inversor rojo. El número de personas de las que recibe 1 000 CZK es igual a la suma de \[3^2 + 3^3 + 3^4 + 3^5 + 3^6\] (toda la pirámide debe tener ocho niveles). Tampoco debemos olvidar restar la tasa de inscripción. Así pues, \[Z_2=3\cdot 6\ 000 + (3^2+3^3 + 3^4 + 3^5 + 3^6 )\cdot 1\ 000 - 20\ 000 = 1\ 087\ 000\,\text{CZK}.\]
La solución del 3.5. Gracias al ejercicio 3.1, sabemos que hay un total de 3 280 personas en la pirámide, cada una de las cuales, salvo el fundador, pagó 20 000 CZK por la tasa de inscripción. Por lo tanto, la recaudación total asciende a 65 580 000 CZK. De las partes 3.3 y 3.4 conocemos el beneficio del fundador y del inversor en el segundo nivel, por lo que calcularemos también el beneficio del inversor en el tercer nivel (de forma similar a la parte 3.4): \[Z_3=3\cdot 6\ 000 + (3^2+3^3 + 3^4 + 3^5 )\cdot 1\ 000 - 20\ 000 = 358\ 000\,\text{CZK}. \] Ahora podemos determinar la parte de los fondos pagados a las personas de los tres primeros niveles (\(S\) es la cantidad total): \[P''=100\cdot\frac{Z_1 + 3\cdot Z_2 + 9\cdot Z_3}{S}=100\cdot\frac{37\ 638\ 000}{65\ 580\ 000}\doteq 57{,}39\ \%.\] Para comprender mejor, es importante darse cuenta de que esta parte del total de los “ingresos de la empresa” se paga a sólo 13 personas de un total de 3280. Aproximadamente \(0{,}4\ \%\) de las personas de la pirámide recibirá, por tanto, más de la mitad del dinero recaudado. No es extraño, por tanto, que las estafas piramidales estén prohibidas como modelo de negocio en varios países del mundo (lamentablemente, la República Checa no se encuentra entre ellos a partir de 2023).
Bibliografía
Yates K. The Math of Life and Death: 7 Mathematical Principles That Shape Our Lives. Scribner; Standard Edition (January 7, 2020).
Illinois Attorney General. Pyramid schemes [online]. Accesible de https://ag.state.il.us/consumers/pyramid.html [cit. 1.6.2023].