Desde el siglo XV, los navegantes disponían de ayudas mecánicas que les permitían medir la distancia angular entre dos objetos (como las estrellas, el Sol y el horizonte, o puntos significativos de una tierra lejana). Entre tales ayudas, mencionamos aquí el vara de Jacob, el astrolabio o el sextante marino.1 Es interesante observar que, a pesar de su antigüedad, el sextante, en particular, todavía tiene su lugar como reserva en caso de pérdida repentina de la señal GPS e incluso se está probando su posible uso de emergencia en el espacio. 2 Entre otras herramientas mecánicas de navegación, mencionemos el trazador de tres brazos, cuya función se explicará en la nota tras la solución del primer ejercicio.
Los dos siguientes ejercicios incluyen un mapa que los alumnos deberán dibujar. Por lo tanto, proporcionamos las tareas también en forma de hojas de trabajo imprimibles.
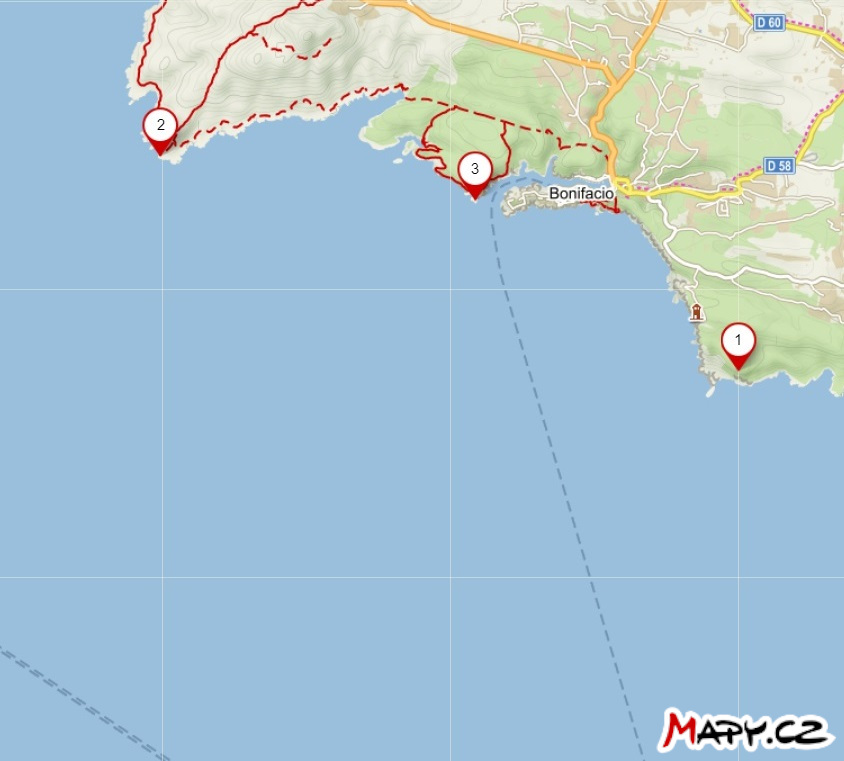
Ejercicio 1. En el mapa están marcadas las posiciones de tres faros cercanos a la ciudad de Bonifacio, en Córcega. EL capitán de un barco en el mar ha medido dos distancias angulares, denotadas \(\theta\), entre dos pares de faros de la siguiente manera:
Construye un punto en el mapa indicando la posición del barco en el momento de medir. Supongamos que las mediciones se realizaron en rápida sucesión, es decir, la posición del barco prácticamente no cambió.
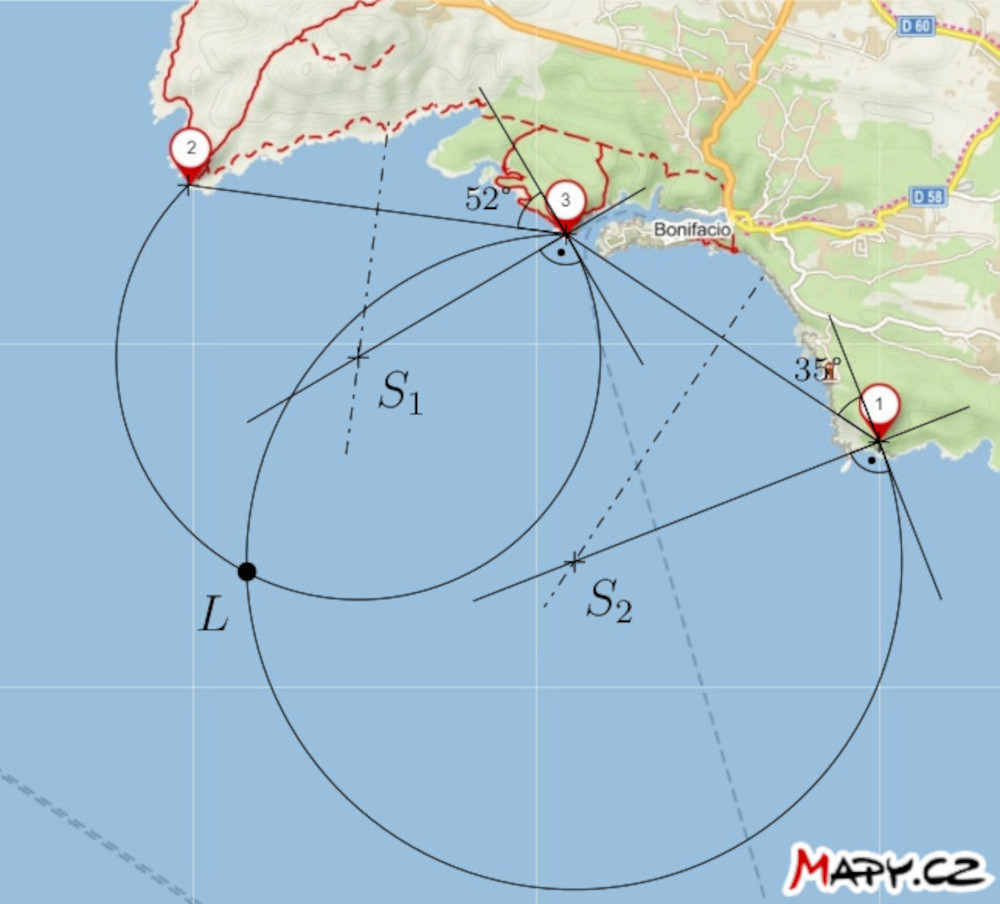
Solución. Si la distancia angular entre los faros 2 y 3 es de 52°, el barco se encuentra en algún punto del círculo que corresponde a un lugar geométrico de un vértice del ángulo 52° que subtiende a un segmento de recta con los puntos extremos 2 y 3. Del mismo modo, también se encuentra en el círculo que es un lugar geométrico de un vértice del ángulo 35° que subtiende un segmento de recta con los puntos extremos 1 y 3. Por lo tanto, el barco debe estar en la intersección de estos dos círculos. Por supuesto, sólo consideramos los arcos circulares que tienen sentido.
Nota. La herramienta que liberó a los navegantes de esta construcción es el (también llamado transportador de tres brazos) que ya hemos mencionado. Sus tres brazos se colocaban en el mapa de forma que pasaban por las posiciones de los tres puntos salientes y formaban ángulos de los tamaños medidos. La intersección de los brazos determinaba entonces la posición del barco en el mapa.
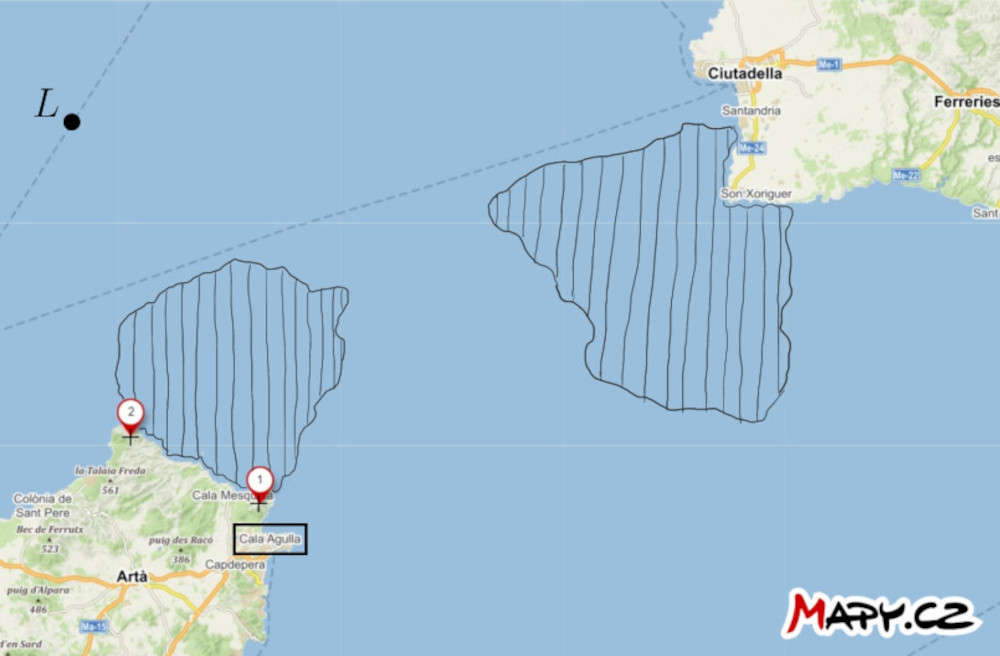
Ejercicio 2. En el mapa del estrecho entre las islas de Mallorca y Menorca, se marcan dos puntos destacados en tierra firme y la posición del barco \(L\) están marcados. Además, dos zonas de aguas peligrosas, con obstáculos submarinos, están indicadas. Encuentra la manera de que el barco navegue a través de las aguas peligrosas hasta el puerto de Cala Agulla. Utiliza la habilidad del capitán de medir la distancia angular entre los dos puntos mencionados en cualquier momento.
Solución. Construyamos los arcos mayores de las circunferencias, denominadas \(k_1\) y \(k_2\) que pasan por los puntos \(1\) y \(2\). Los centros de las circunferencias están en el eje del segmento de recta con puntos extremos \(1\) y \(2\). Las circunferencias tienen la siguiente propiedad adicional: el arco de la circunferencia \(k_1\) encierra estrechamente la zona peligrosa más cercana al del puerto, y el arco de la circunferencia \(k_2\) es tangente a la zona más alejada. Cada uno de estos arcos es un subconjunto de algún lugar de un vértice de un ángulo que subtiende al segmento de recta con extremos \(1\) y \(2\). Ahora midamos los ángulos inscritos correspondientes a estos arcos. En nuestra situación, el ángulo es de aproximadamente \(33°\) para el arco de círculo \(k_1\) y \(20°\) para el arco de círculo \(k_2\).
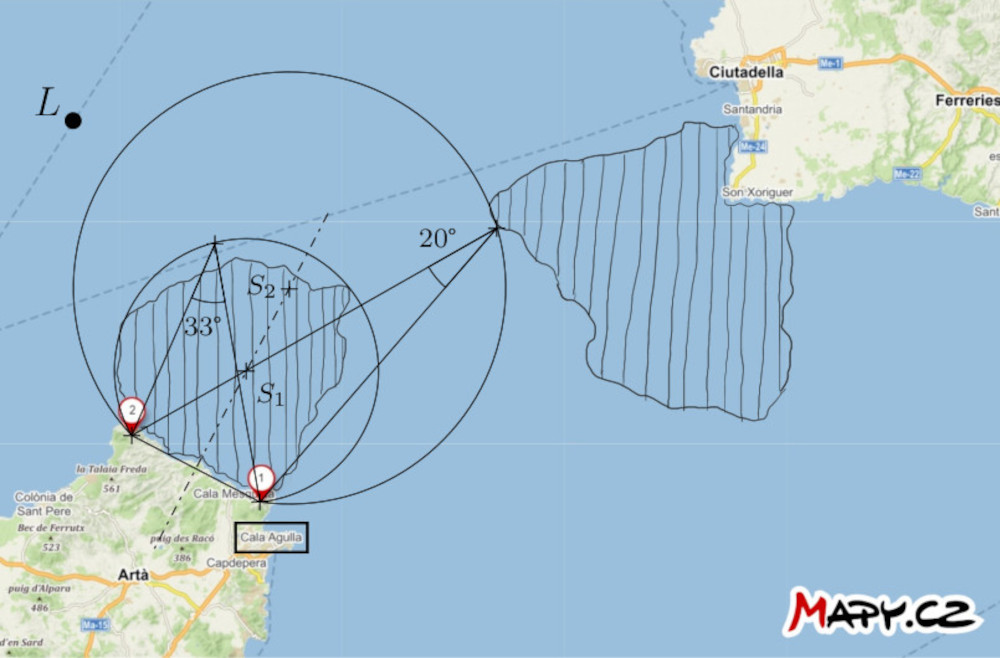
Si la distancia angular entre los puntos \(1\) y \(2\) con respecto al barco es inferior a \(33°\), podemos decir que el barco está con seguridad fuera de la zona de peligro más próxima al puerto. Por el contrario, si la distancia angular es superior a \(20°\), el barco está fuera de la zona de peligro más lejos del puerto.
Formulemos ahora una estrategia de navegación: El capitán del barco debe dirigirse en línea recta hacia el punto \(2\) y medir la distancia angular entre los puntos \(1\) y \(2\) durante el trayecto. Cuando esta distancia sea superior a \(20°\) pero inferior a \(33°\), el barco deberá girar a la izquierda en la dirección de navegación, para navegar alrededor de la zona de peligro, manteniendo la distancia angular entre los dos puntos relativos al barco entre \(20°\) y \(33°\). Este enfoque garantiza que el barco permanezca en la zona segura entre los dos arcos.
