Již od 15. století byli navigátoři vybaveni mechanickými pomůckami, které jim umožňovaly změřit úhlovou vzdálenost dvou objektů (např. hvězd, Slunce a horizontu nebo význačných bodů na vzdálené pevnině). Z takových pomůcek zde zmíníme např. Jakubovu hůl, astroláb nebo námořní sextant.1 Jako zajímavost poznamenejme, že i přes své stáří má konkrétně sextant stále své místo jako záloha při náhlém výpadku signálu GPS a dokonce se testuje i jeho potenciální nouzová využitelnost ve vesmíru.2 Z dalších navigačních mechanických pomůcek zmiňme např. trojramenný úhloměr, jehož role bude objasněna v poznámce po první vyřešené úloze.
V zadání následujících dvou úloh je mapa, do které žáci budou rýsovat, přikládáme proto zadání také ve formě tisknutelného pracovního listu.
Úloha 1. Na mapě jsou vyznačeny polohy tří majáků blízko města Bonifacio na Korsice. Kapitán lodi na moři změřil dvě úhlové vzdálenosti \(\theta\) dvojice majáků následovně:
Sestrojte na mapě bod označující polohu lodi v čase měření. Předpokládejme, že měření proběhla rychle za sebou, tzn. poloha lodi se prakticky nezměnila.
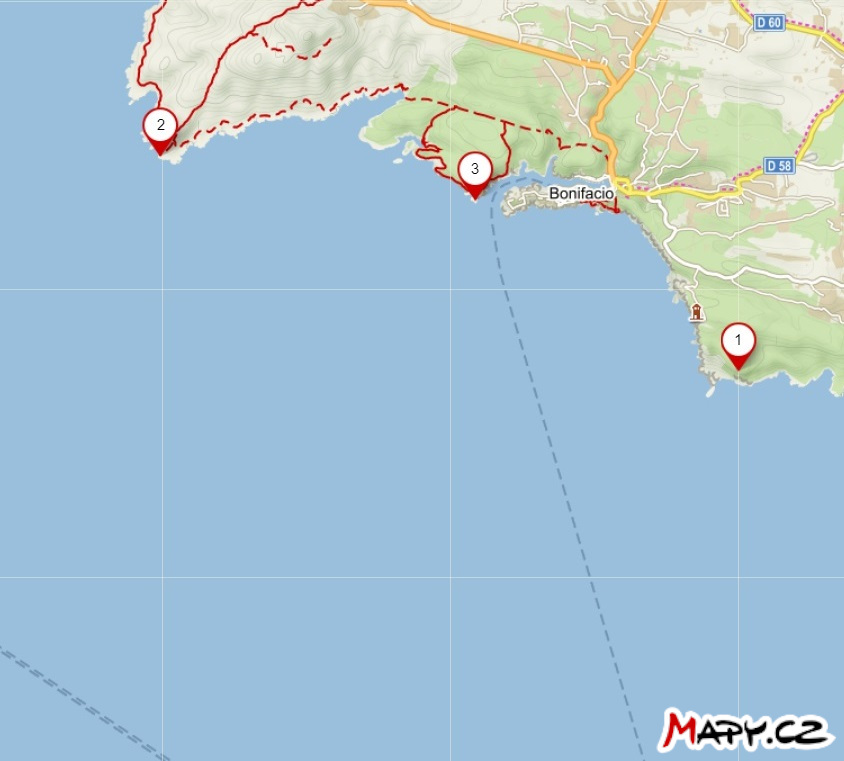
Řešení. Jestliže úhlová vzdálenost mezi majáky \(2\) a \(3\) činí \(52°\), nachází se loď někde na ekvigonále (tj. množině bodů v rovině, z kterých je danou úsečku vidět pod daným úhlem) úsečky s koncovými body \(2\) a \(3\) příslušné řečenému úhlu. Podobně se také nachází na ekvigonále úsečky s koncovými body \(1\) a \(3\) příslušné úhlu \(35°\), tedy se loď musí nacházet v průsečíku dvou ekvigonál. Samozřejmě bereme v úvahu pouze ty kruhové oblouky, které dávají smysl.
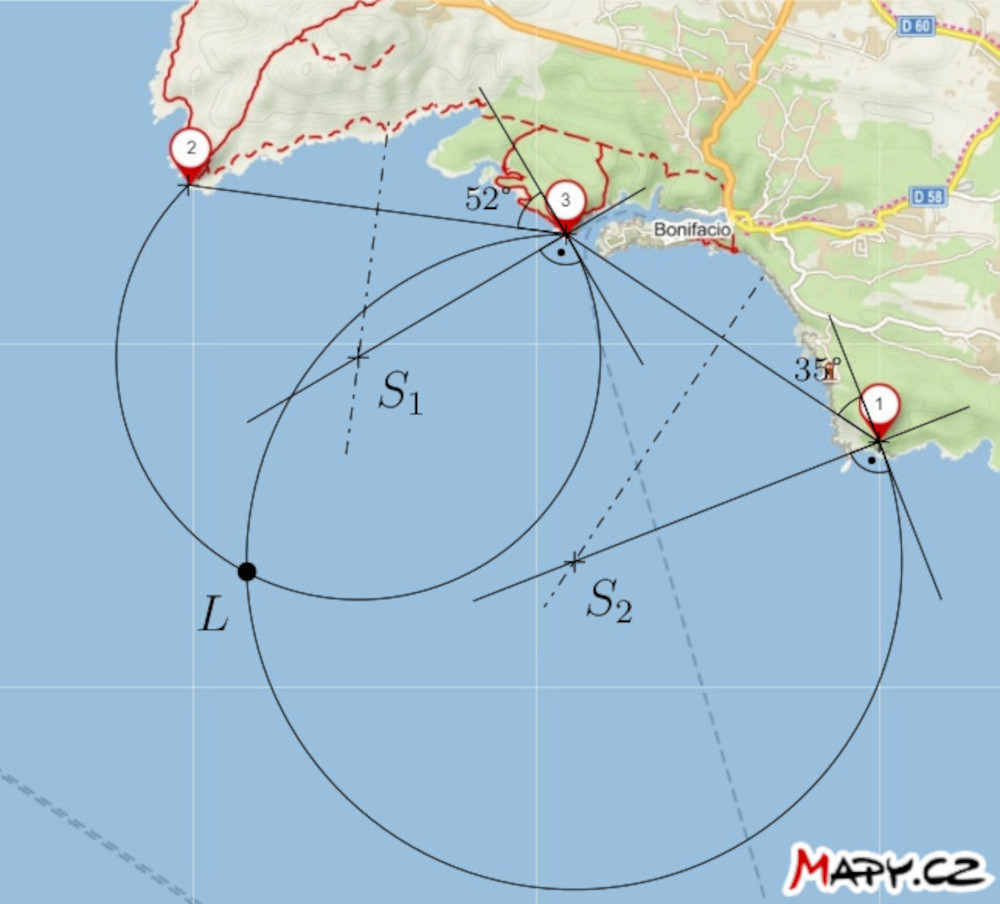
Poznámka. Pomůcka, která navigátory zbavila nutnosti konstrukce, je již zmíněný trojramenný úhloměr, jehož tři ramena se nastavila na mapě tak, ať prochází třemi polohami význačných bodů a svírají úhly o naměřených velikostech. Průsečík ramen pak určil polohu lodi na mapě.
Úloha 2. Na mapě úžiny mezi ostrovy Mallorca a Menorca jsou vyznačeny dva výrazné body na pevnině a poloha lodi \(L\). Kromě toho se také na moři nachází dvě oblasti nebezpečných vod, ve kterých se nachází podvodní překážky. Najděte způsob, jak proplout lodí nebezpečnými vodami do přístavu Cala Agulla. Využijte toho, že kapitán lodi umí v libovolném okamžiku změřit úhlovou vzdálenost dvou řečených bodů.
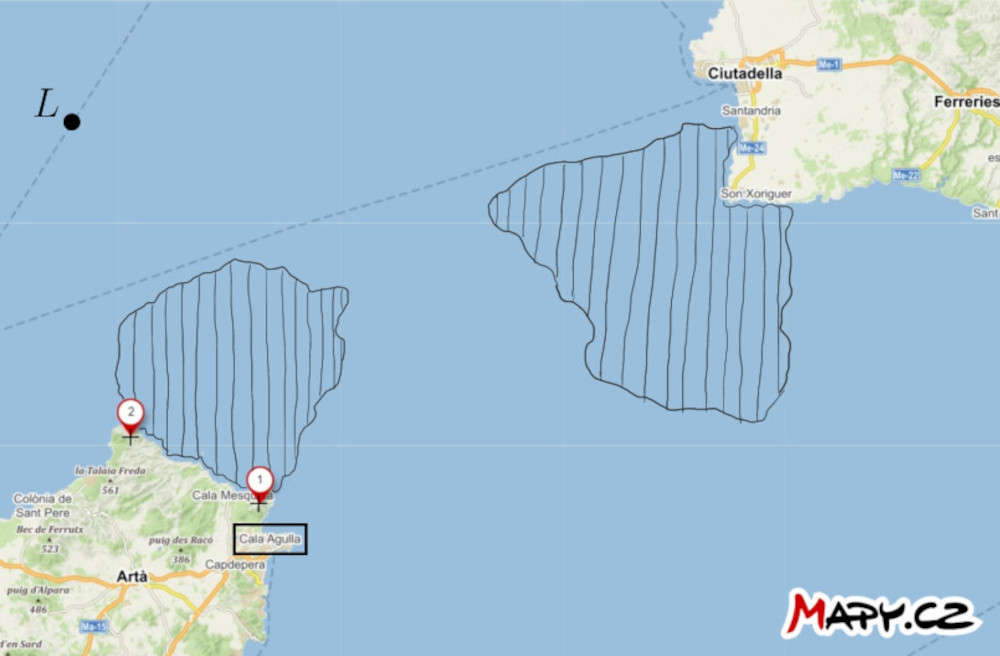
Řešení. Sestrojme větší oblouky kružnic \(k_1\) a \(k_2\), které prochází body \(1\) a \(2\) (tedy mají střed na ose úsečky s koncovými body \(1\) a \(2\)) a které mají následující další vlastnost: oblouk kružnice \(k_1\) těsně uzavírá přístavu bližší nebezpečnou oblast a oblouk kružnice \(k_2\) se dotýká vzdálenější oblasti. Každý z těchto oblouků je přitom podmnožinou nějaké ekvigonály úsečky \(12\). Změřme nyní obvodové úhly příslušné těmto obloukům – u našeho zadání je to přibližně \(33°\) pro oblouk kružnice \(k_1\) a \(20°\) pro oblouk kružnice \(k_2\).
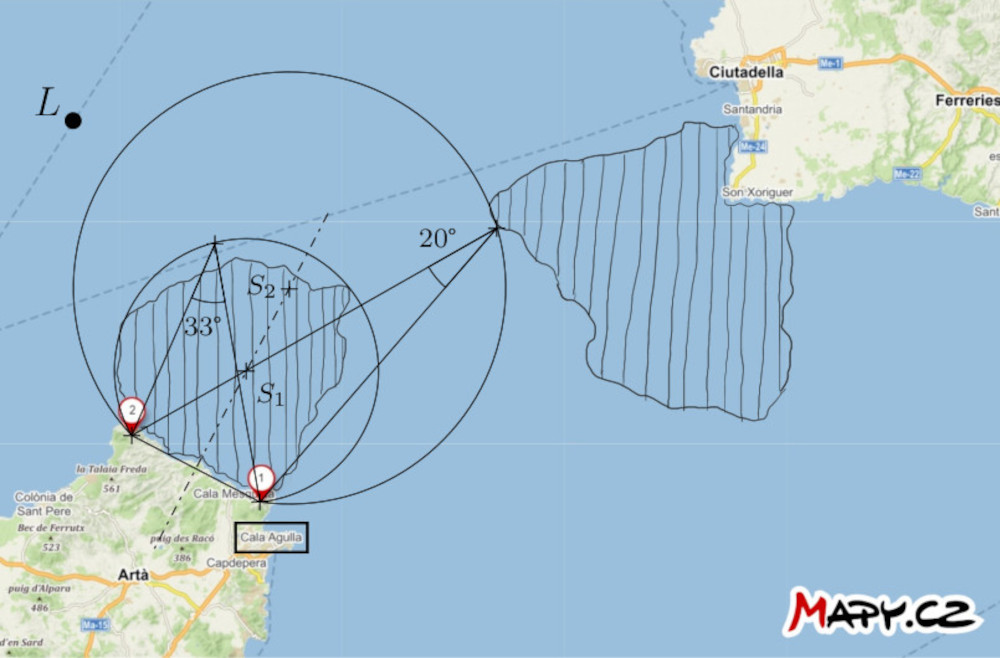
Jestliže je oblouková vzdálenost bodů \(1\) a \(2\) vzhledem k lodi menší než \(33°\), můžeme říci, že se loď nachází s jistotou mimo nebezpečnou oblast bližší přístavu. Naopak, jestliže bude řečená oblouková vzdálenost větší než \(20°\), loď se nachází mimo nebezpečnou oblast vzdálenější přístavu.
Formulujme nyní strategii proplutí: Kapitán lodi zamíří přímou cestou např. k bodu \(2\) a během plavby měří obloukovou vzdálenost bodů \(1\) a \(2\). Až bude tato vzdálenost větší než \(20°\) (ale stále menší než \(33°\)), stočí loď vlevo ve směru plavby a obepluje nebezpečné místo tak, že úhlovou vzdálenost obou bodů vzhledem k lodi udržuje mezi \(20°\) a \(33°\). Tak je zajištěno, že loď zůstane v bezpečné oblasti mezi oběma oblouky.
