Since the 15th century, navigators have been equipped with mechanical aids, that allowed them to measure the angular distance between two objects (such as stars, the Sun, and the horizon, or significant points on a distant land). Among such aids, we mention here the Jacob’s staff, the astrolabe, or the marine sextant.1 It is interesting to note that despite its age, the sextant, in particular, still has its place as a backup in case of a sudden loss of GPS signal and is even being tested for its potential emergency use in space. 2 Among other mechanical navigation tools, let us mention the station pointer, whose role will be explained in the note after the solution of the first exercise.
The following two exercises involve a map that students will need to draw on. Therefore, we provide the assignments also in the form of a printable worksheets.
Exercise 1. On the map, the positions of three lighthouses near the town of Bonifacio on Corsica are marked. The captain of a ship at sea has measured two > angular distances, denoted \(\theta\), between two pairs of lighthouses as follows:
Construct a point on the map indicating the position of the ship at the time of measurement. Assume that the measurements were taken in rapid succession, i.e., the ship’s position practically did not change.
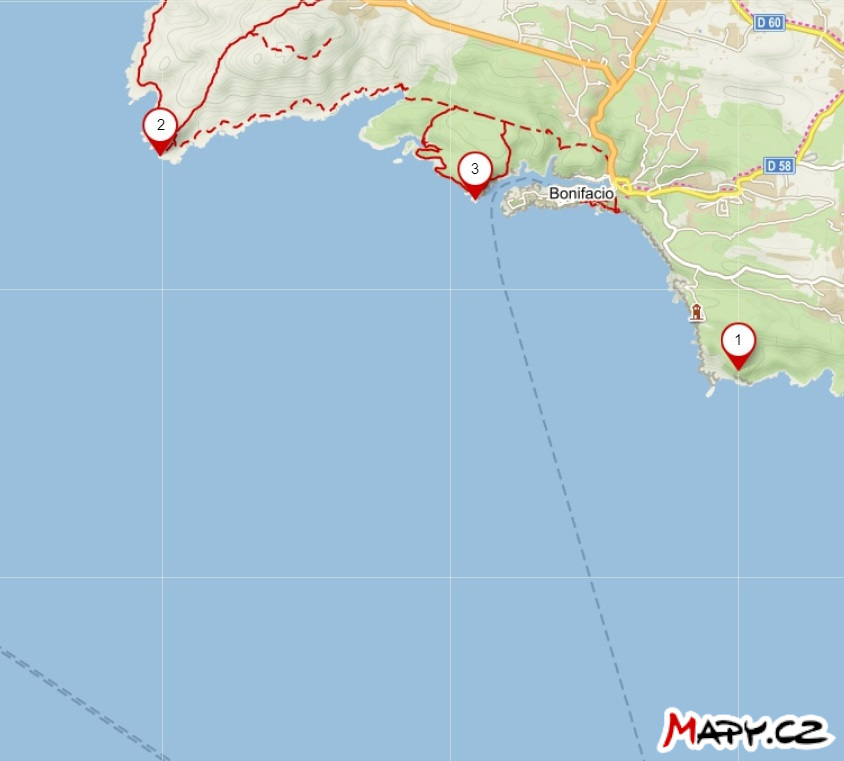
Solution. If the angular distance between lighthouses 2 and 3 is 52°, the ship is located somewhere on the circle that corresponds to a locus of a vertex of the angle 52° subtending a line segment with endpoints 2 and 3. Similarly, it is also located on the circle that is a locus of a vertex of the angle 35° subtending a line segment with endpoints 1 and 3. So, the ship must be at the intersection of these two circles. Of course, we only consider those circular arcs that make sense.
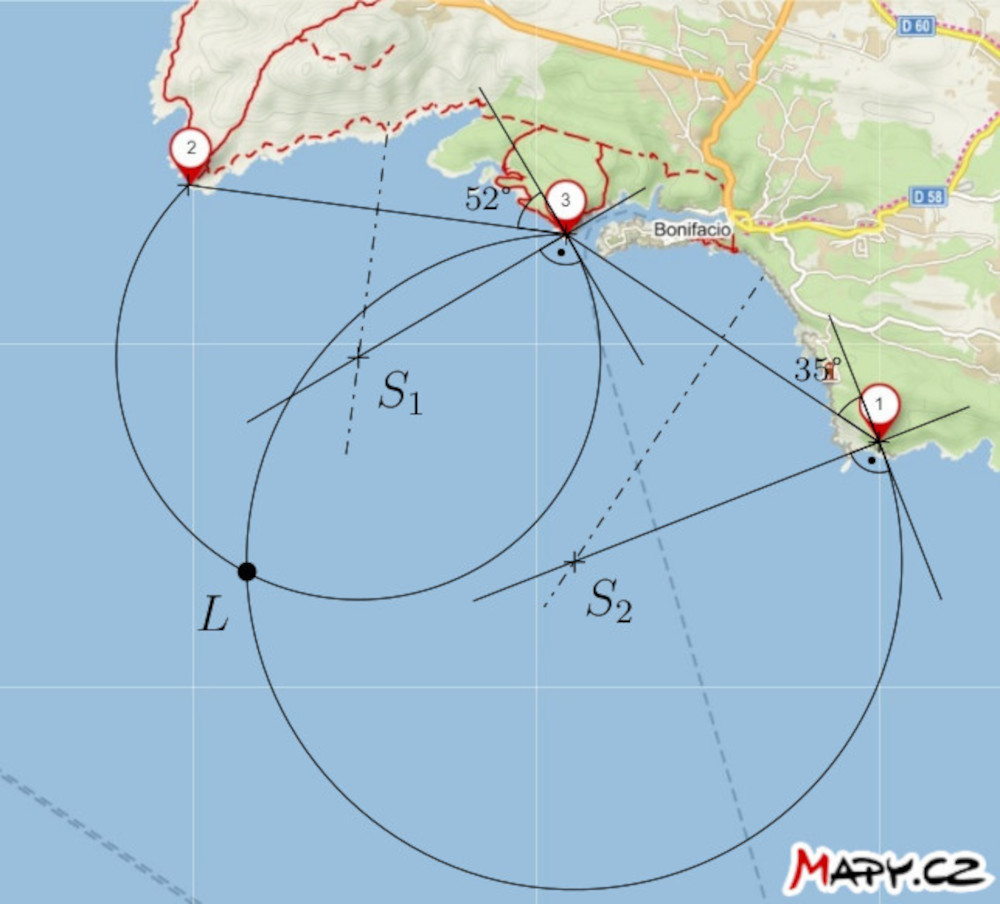
Note. The tool that freed navigators from this construction is the station pointer (also called the three-armed protractor) we already mentioned. Its three arms were set on the map in such a way that they passed through positions of the three salient points and formed angles of the measured sizes. The intersection of the arms then determined the position of the ship on the map.
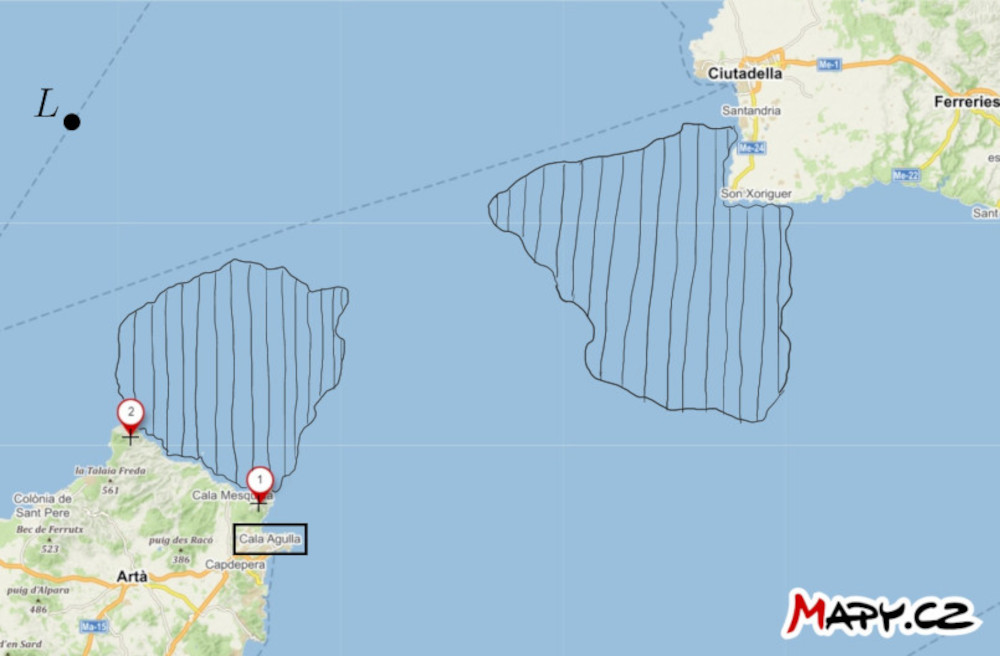
Exercise 2. On the map of the strait between the islands of Mallorca and Menorca, two prominent points on the mainland and the position of the ship \(L\) are marked. Additionally, two areas of dangerous waters, containing underwater obstacles, are indicated. Find a way for the ship to navigate through the dangerous waters to the port of Cala Agulla. Utilize the ship captain’s ability to measure the angular distance between the two mentioned points at any given moment.
Solution. Let us construct the larger arcs of the circles, denoted \(k_1\) and \(k_2\) passing through points \(1\) and \(2\). The centers of the circles are on the axis of the line segment with endpoints \(1\) and \(2\). The circles have the following additional property: the arc of circle \(k_1\) tightly encloses the dangerous area closer to the port, and the arc of circle \(k_2\) is tangent to the more distant area. Each of these arcs is a subset of some locus of a vertex of an angle subtending the line segment with endpoints \(1\) and \(2\). Now, let us measure the inscribed angles corresponding to these arcs. In our situation, the angle is approximately \(33°\) for the arc of circle \(k_1\) and \(20°\) for the arc of circle \(k_2\).
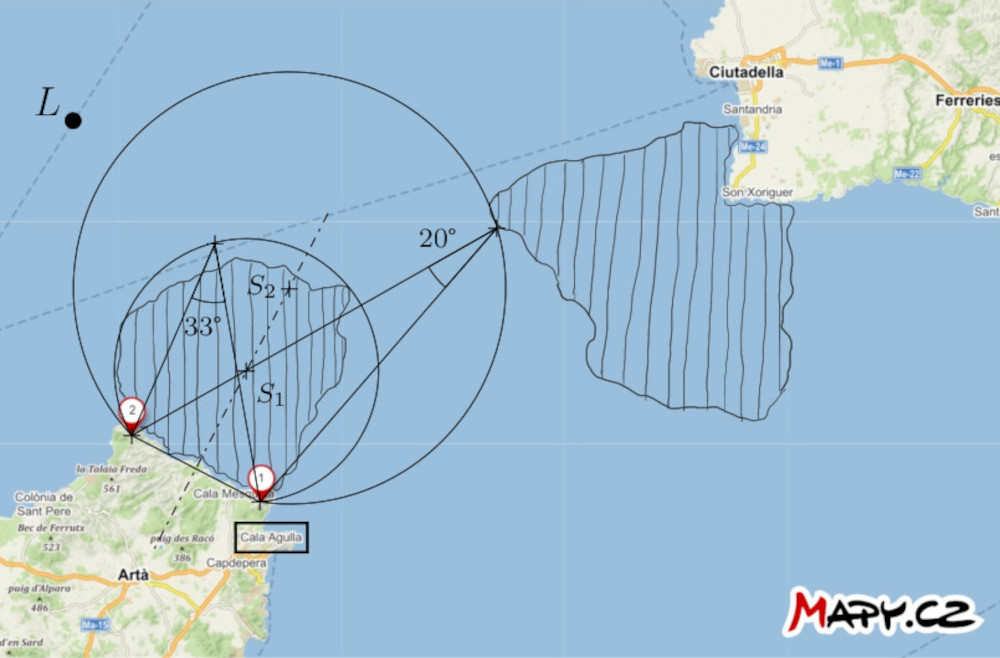
If the angular distance between points \(1\) and \(2\) with respect to the ship is less than \(33°\), we can say that the ship is confidently outside the danger zone closer to the port. Conversely, if the angular distance exceeds \(20°\), the ship is outside the danger zone farther from the port.
Now, let us formulate a strategy for navigation: The captain of the ship should head in a straight direction towards point \(2\) and measure the angular distance between points \(1\) and \(2\) during the journey. When this distance becomes greater than \(20°\) but still less than \(33°\), the ship should turn left in the direction of sailing, to navigate around the danger zone, by maintaining the angular distance between the two points relative to the ship between \(20°\) and \(33°\). This approach ensures that the ship remains in the safe area between the two arcs.
