V tomto textu bude ukázáno jak může analytická geoemtrie přispět k monitoringu zdravotního stavu stromů. Nejprve si připomeneme důležitost stromů v městském prostředí a představíme určité nesnáze s diagnostikou zdravotního stavu těchto stromů. Poté si ukážeme, jak je možné pomocí analytické geometrie spojit dvě diagnostické metody do jednotného celku a získat tak komplexnější informaci pro posouzení rizika pádu stromu.
Stromy jsou důležitým prvkem, který činí život v městské zástavbě příjemnějším. Poskytují stín a kyslík, omezují prašnost a hluk, snižují teplotu v okolí a poskytují útočiště pro ptáky a další živočichy.
Umístění stromů do městské zástavby je však spojeno s riziky. Jedním z rizik s nejhorším dopadem je riziko pádu stromu. Pád stromu může způsobit zranění osob, poškození majetku a v nejhorším případě i smrt. Proto je důležité pravidelně kontrolovat zdravotní stav stromů a včas odhalit případné problémy.
Arboristé, odborníci na péči o dřeviny mimo les, používají různé metody pro diagnostiku zdravotního stavu stromů. Mezi tyto metody patří například akustický tomograf, který umožňuje posoudit stav dřeva v kmeni stromu neinvazivně, bez nutnosti poškození stromu. Je to jakési CT vyšetření stromů, které umožňuje odhalit skryté vady a degradaci dřeva. Na rozdíl od lékařského CT vyšetření, akustický tomograf využívá zvukové vlny, které mají velkou vlnovou délku a s tím jsou spojena omezení daná fyzikálními principy šíření vlnění. Jedním z důsledků je, že akustický tomograf neumožňuje s dostatečnou jistotou rozlišit mezi stromem s dutinou a stromem s prasklinou. Oba defekty se při vyšetření tomografem jeví jako místo, ve kterém se zvuk šíří pomaleji než v okolním zdravém dřevě. Velikost praskliny však často bývá nadhodnocena a může se zobrazovat podobně jako dutina. Při kontrole stromů je proto vhodné používat i další doplňkové metody, které umožňují získat komplexnější informace o zdravotním stavu stromu.
Jednou z těchto metod je resistograf, který měří tuhost dřeva a pomáhá odhalit skryté vady. Resistograf je přístroj, který pomocí vrtáku a měření odporu dřeva umožňuje posoudit jeho strukturu a mechanické vlastnosti. Protože je vrták velmi tenký, je tato metoda poměrně málo invazivní a nepoškozuje strom. Resistograf dokáže detekovat praskliny, dutiny a další vady v dřevě a takto získaná data mohou být použita k doplnění informací získaných z akustického tomografu.
V praxi probíhá diagnostika stromů obvykle tak, že se nejprve provede měření pomocí akustického tomografu, který poskytne základní informace o stavu dřeva v kmeni. Následně se provede měření pomocí resistografu, které umožní získat doplňující informace o stavu dřeva a odhalit případné skryté vady. Tímto způsobem je možné získat komplexní obraz o zdravotním stavu stromu a včas odhalit případné problémy.
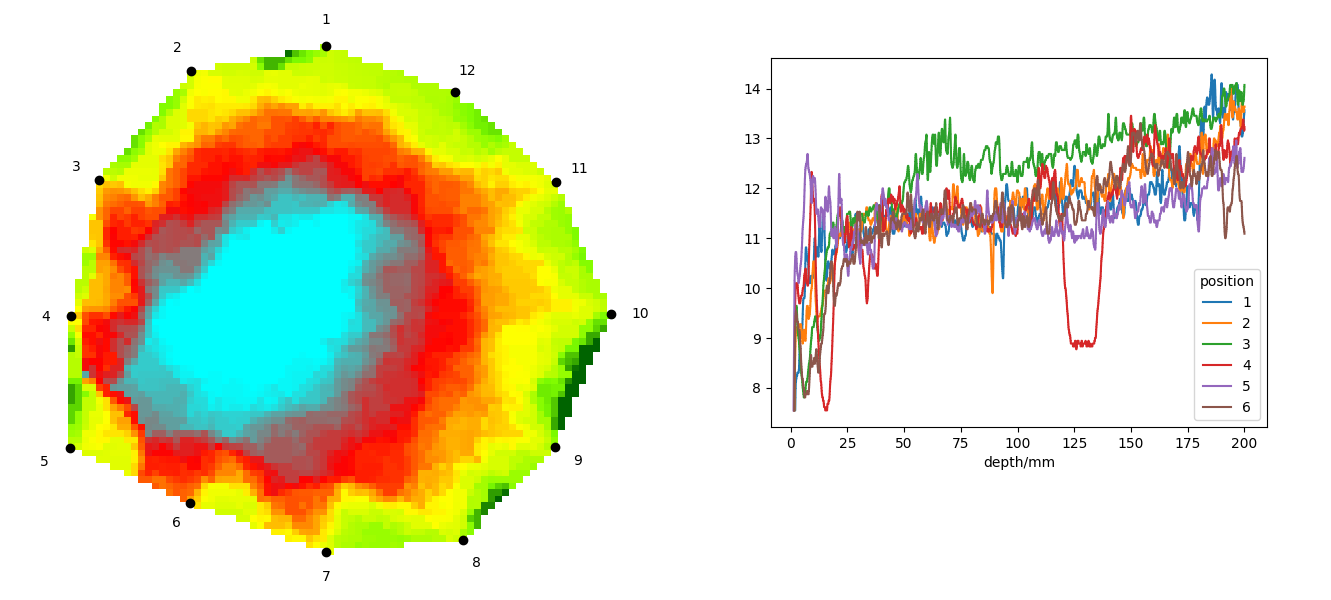
Následující obrázek ukazuje možné výstupy z akustického tomografu a resistografu. Na obrázku vlevo je rekonstrukce obrazu z akustického tomografu, která ukazuje rychlost šíření zvuku v dřevě. Tato rychlost nás zajímá, protože přímo souvisí s mechanickými vlastnostmi dřeva. Modré a červené oblasti představují místa, kde se zvuk šíří pomaleji, v zelené oblasti se zvuk šíří rychleji. Vpravo je výstup z resistografu, který ukazuje výkon nutný pro udržení konstantních otáček vrtáku a je také mírou mechanické pevnosti dřeva. Vrtání bylo provedeno vždy mezi dvěma senzory akustického tomografu, takže mezi dvanácti senzory tomografu bylo provedeno dvanáct vrtů resistografem.

V obrázku vidíme, že jedna z křivek resistografu má znatelný pokles v hloubce cca 125 milimetrů. Tento pokles odpovídá dutině o velikosti přibližně jeden centimetr, akustický tomograf však ukazuje dutinu rozsáhlejší. Pro pohodlné zpracování dat je vhodné data spojit do jednoho obrázku. Proto bychom rádi měli v tomogramu (výstupu z akustického tomografu) zobrazeny i pozice vrtů a údaje z resistografu.
Při problematice spojení dat z obou metod nastupuje do hry matematika. Předpokládejme, že vrtání probíhalo ze středu spojnice dvou sousedních senzorů a směřovalo do středu kmene stromu. Hodnoty rezistografu budeme znázorňovat intenzitou šedi a výsledný obrázek bude kompozicí tomogramu a sloupce s proměnnou intenzitou šedi.
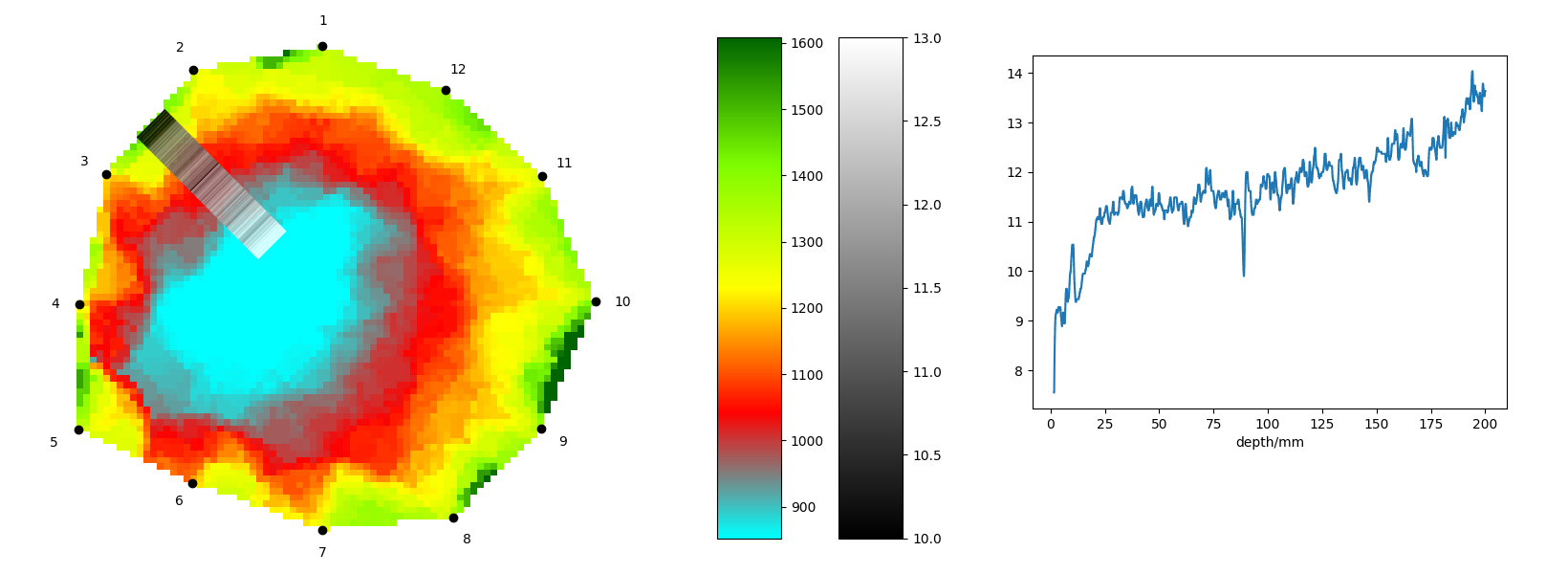
Tomogram je obvykle umístěn do souřadné soustavy tak, že střed tomogramu leží v počátku, první senzor leží na kladné části osy \(y\) a další senzory se číslují proti směru hodinových ručiček. Pro vytvoření sloupce s daty z resistografu mezi druhým a třetím senzorem je z matematického hlediska nutné znát funkci, která převede hloubku z křivky resistografu (depth) na pozici v souřadné soustavě spojené s tomogramem. Grafem takové funkce bude přímka jdoucí ze středu spojnice senzorů do středu stromu. Označme tuto přímku \(p\).
Jednotlivé kroky pro nalezní vhodné rovnice přímky \(p\) mohou být následující.
Vyzkoušejme si tento postup na konkrétním příkladu, který se vztahuje ke geometrii z Obrázku 1.
Úloha 1. Souřadnice bodů, ve kterých byly umístěny senzory číslo 2 a 3 akustického tomografu, jsou \(P_2=[-15, 26]\) a \(P_3=[-25, 14]\). Souřadnice středu tomogramu jsou \(O=[0, 0]\).
Najděte parametrické vyjádření přímky \(p\) jdoucí bodem \(A\) a středem tomogramu \(O\), při kterém bude hodnota parametru rovna hloubce vrtu.
Řešení. Střed \(A\) úsečky mezi body \(P_2\) a \(P_3\) vypočteme podle vztahu
\[ A = \frac{P_2 + P_3}{2}.\]
Po dosazení souřadnic získáme \(A=[-20, 20]\).
Směrový vektor \(\vec u\) přímky \(p\) určíme pomocí bodů \(O\) a \(A\), kterými přímka \(p\) prochází jako \[\vec u = O-A,\] v souřadnicích \(\vec u = [0,0] - [-20, 20] = (20, -20)\).
Délka vektoru \(\vec u=(u_1, u_2)\) je podle Pythagorovy věty \[|\vec u| = \sqrt{u_1^2 + u_2^2} = \sqrt{20^2 + (-20)^2} = \sqrt{800} = 20\sqrt{2}.\]
Jednotkový vektor \(\vec e\) ve směru vektoru \(\vec u\) určíme jako podíl vektoru a jeho délky, \[\vec e = \frac{\vec u}{|\vec u|} = \left(\frac{20}{20\sqrt{2}}, \frac{-20}{20\sqrt{2}}\right) = \left(\frac{1}{\sqrt{2}}, \frac{-1}{\sqrt{2}}\right).\]
Výsledná parametrická rovnice přímky \(p\) je tedy \[ \begin{align*} x &= -20 + t \cdot \frac{1}{\sqrt{2}}, \\ y &= 20 - t \cdot \frac{1}{\sqrt{2}}, \qquad t\in\mathbb R. \end{align*} \]
Úloha 2. Modifikujte postup z Úlohy 1 tak, aby vrt byl kolmý k úsečce definované senzory akustického tomografu.
Řešení. Je nutné nahradit vektor \(\vec u\) směrovým vektorem kolmým na úsečku definovanou senzory akustického tomografu. Směrové vektory kolmé k vektoru \(\vec v = (v_1,v_2)\) jsou \((-v_2,v_1)\) a \((v_2,-v_1)\). Vektor z bodu \(P_2\) do bodu \(P_3\) má souřadnice \[\vec v = P_3 - P_2 = (-25, 14) - (-15, 26) = (-10,-12).\] V našem případě máme pro kolmici k tomuto vektoru možnosti \[ \vec n_{1} = (12, -10), \quad \vec n_{2} = (-12, 10). \] Z Obrázku 2 je vidět, že směrový vektor má směřovat doprava a dolů, použijeme tedy vektor \(\vec n_{1}\). Délka vektoru \(\vec n_{1}\) je dána vztahem \[|\vec n_{1}| = \sqrt{12^2 + (-10)^2} = \sqrt{244} = 2\sqrt{61}\] a jednotkový vektor ve směru vektoru \(\vec n_{1}\) je podílem vektoru a jeho délky, tj. \[\vec e = \frac{\vec n_{1}}{|\vec n_{1}|} = \left(\frac{12}{2\sqrt{61}}, \frac{-10}{2\sqrt{61}}\right) = \left(\frac{6}{\sqrt{61}}, \frac{-5}{\sqrt{61}}\right).\]
Parametrická rovnice přímky \(p\) je tedy \[ \begin{align*} x &= -20 + t \cdot \frac{6}{\sqrt{61}}, \\ y &= 20 - t \cdot \frac{5}{\sqrt{61}}, \qquad t\in\mathbb R. \end{align*} \]
Poznámka. Postup uvedený v předchozích úlohách je možné použít pro libovolné dva senzory akustického tomografu a je možné jej snadno algoritmizovat. Výstupem poté bude spojení dat z resistografu a akustického tomografu do jednoho obrázku.
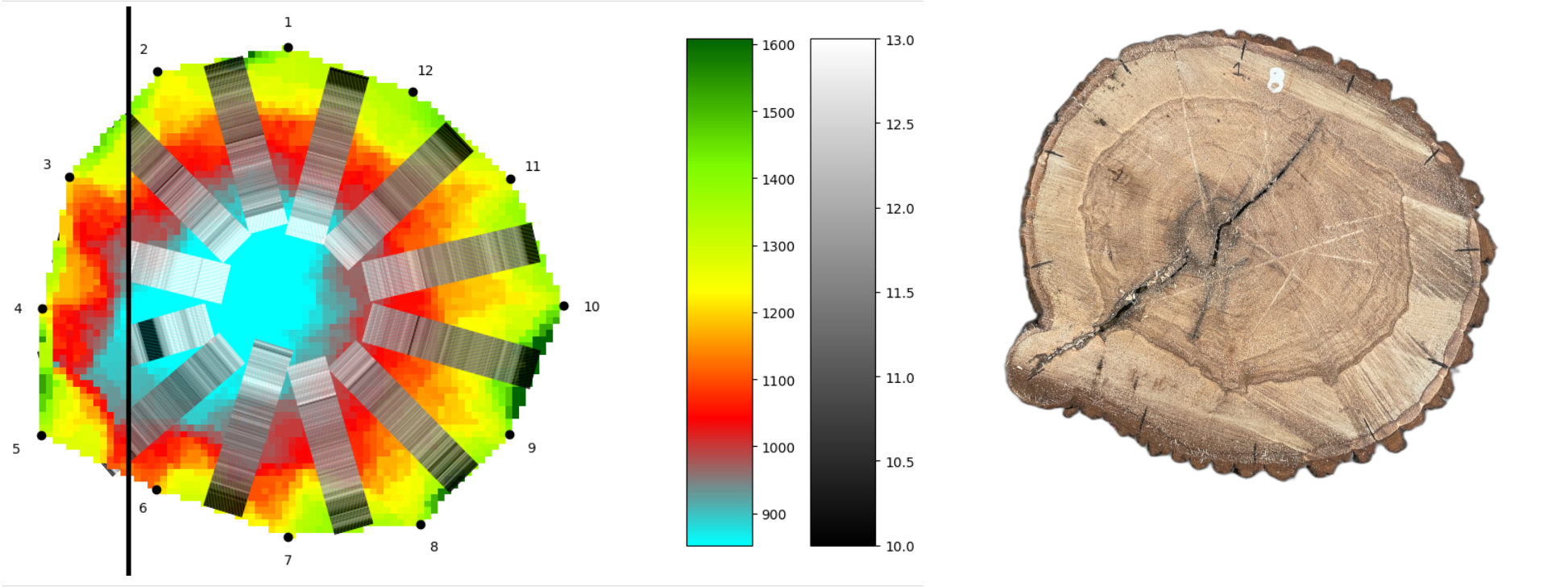
Data a fotky v tomto textu pochází z reálných měření, která byla provedena na stromech ve Valdštejnské lipové aleji v Jičíně. Jedná se o nejstarší lipové stromořadí v ČR a jeho délka je přes 1700 metrů. Vzhledem k tomu, že ne všechny stromy jsou v dobrém zdravotním stavu, je nutné pravidelně kontrolovat jejich zdravotní stav. V rámci monitoringu byly některé stromy vybrány ke kácení a na těchto stromech byla před skácením provedena měření. Díky tomu se naskytla jedinečná možnost porovnat výstupy měření s reálným stavem. Tato měření provedl arborista Vojtěch Semík a data byla zpracovávána v rámci ERC CZ projektu DYNATREE (https://starfos.tacr.cz/cs/projekty/LL1909).
V tomto textu jsme se seznámili s možnostmi aplikace aparátu analytické geometrie při spojení dat z akustického tomografu a resistografu. Ukázali jsme si, jak využít parametrickou rovnici přímky k převedení hloubky vrtu z resistografu na souřadnice v souřadné soustavě tomogramu. Tento postup je možné použít pro zpřesnění předpovědi zdravotního stavu stromů a pro získání komplexního obrazu o zdravotním stavu stromu. Spojení dat z obou metod umožňuje získat přesnější informace o stavu dřeva a odhalit případné skryté vady, což je důležité pro zdraví stromů a bezpečnost v městské zástavbě.