
Origami, když slyšíme toto slovo, představíme si asi nejdříve papírovou skládanku ve tvaru zvířete. Existují origami, které zvládne složit malé dítě, ale je i mnoho takových, které zaberou několik hodin či dokonce dní skládání. I život kolem nás a v nás závisí na schopnostech různých materiálů a struktur skládat se. Například okvětní lístky květů, když se rozvíjejí z poupat, křídla hmyzu složená pod krovkami, struktura naší DNA, nebo stěny tlustého střeva.
Origami zažilo v posledních letech velký rozvoj, a to nejen u nadšenců skládajících různé objekty z papíru, ale i v mnoha vědních oborech. Ovlivnilo architekty, designéry nábytku, umělce a vědce.
Jedna z oblastí, kde origami našlo uplatnění, je vesmírný program. Při přepravě rozměrných objektů ve vesmíru je třeba, aby se daly složit do menších rozměrů. Jeden z těchto objektů je starshade, což je vlastně obrovské stínidlo na hvězdy. Astronomové ho potřebují k pozorování planet, které se vyskytují v blízkosti zářivých hvězd. Jejich jasné světlo totiž pozorování znemožňuje.
Výhodné je také použití origami v robotice. Roboti, jejichž konstrukce je založená na origami, mají potenciál být rychlejší, levnější a snadněji vyrobitelní než roboti vytvoření pomocí tradičních výrobních postupů.
Vznikají nové druhy materiálů používající origami struktury. Vzory těchto origami jsou často založeny na pravidelném dělení plochy. Na ně se zaměříme v následujících úlohách.
Jeden z nejznámějších skladů v origami je tzv. Miura-ori nebo Miura fold. Tuto techniku skládání vynalezl japonský astrofyzik Koryo Miura. Po otevření struktury se zdá, že je rovnoměrně rozdělena na šachovnici rovnoběžníků.
U tohoto konkrétního vzoru existuje jeden jednoduchý způsob, jak jej otevřít nebo zavřít. Zatáhnete za jeden roh a origami se otevře s minimálním úsilím. Miura zamýšlel tento způsob skládání pro solární panely a v roce 1995 byl solární panel s touto konstrukcí rozložen na japonské družici Space Flyer Unit. Od té doby našla tato technika skládání mnoho dalších aplikací, využívají ji například některé cestovní solární panely, nebo skládací neprůstřelné štíty pro policejní složky. Tímto způsobem se také například v Japonsku skládají mapy, aby nedocházelo k obvyklému opotřebení v rozích.
Vzor je také využíván v materiálovém inženýrství jako vnitřní část sendvičové struktury. Pokud je vyroben z kevlarové papírenské konstrukce, vláknité desky nebo plastové fólie a vložen mezi dva krycí listy, vznikne lehká konstrukce, která je velmi pevná a stabilní.
Zkusme si tento vzor složit. Začít můžeme třeba s obvyklým formátem papíru \(A4\), který má rozměr \(210\,\text{mm}\) x \(297\,\text{mm}\). Pro plynulé rozevírání a zavírání vzoru je vhodné rozdělit strany na lichý počet dílků. Začneme tím že kratší rozměry formátu \(A4\) rozdělíme na 5 stejně velkých dílků, jeden dílek tedy bude mít délku \(42\,\text{mm}\). Body ležící naproti sobě spojíme a papír v těchto spojnicích poskládáme do tvaru harmoniky.

Jednu z delších hran nyní rozdělíme na 7 dílků. Libovolným bodem dělení povedeme úsečku, která svírá jiný než pravý úhel s delší hranou. Ostatními body dělení vedeme rovnoběžky s touto úsečkou.

V těchto vzájemně rovnoběžných úsečkách harmoniku přehneme. Nyní máme všechny potřebné sklady výsledného vzoru, některé jsou ale ohnuté jiným směrem, než potřebujeme.

Harmoniku rozložíme a přeskládáme tak, aby se z jednotlivých lomených čar staly hřebeny a údolí a to střídavým způsobem.

Hrany vzoru Miura Ori se v origami naznačují tak, jak na následujícím obrázku, tedy hřebeny plně, údolí čárkovaně.
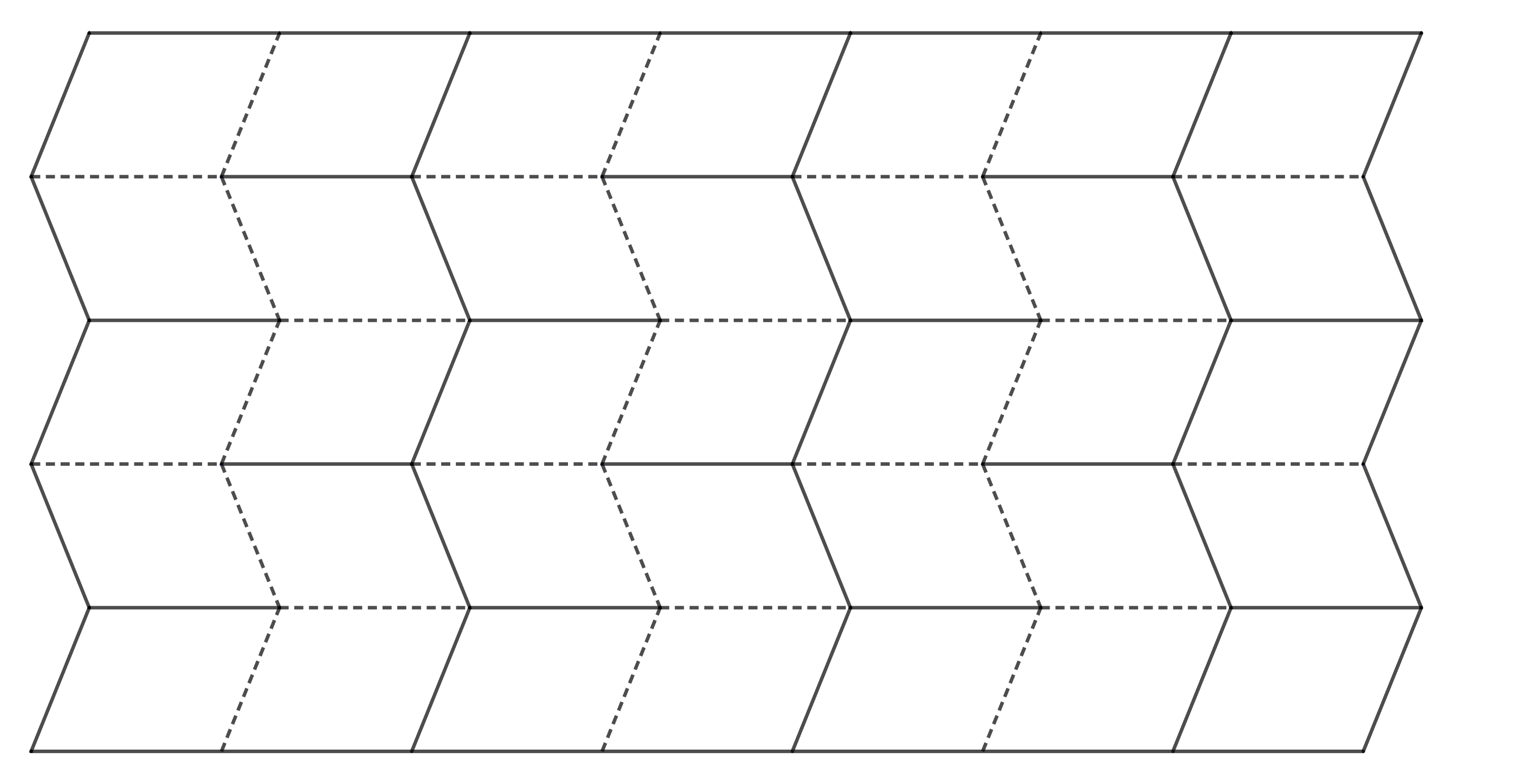
Úloha 1. Na obrázku níže jsou dvě varianty, jak může výsledný vzor ve složeném tvaru vypadat (při stéjném výchozím formátu papíru a stejném počtu dílků dělení). Na jakých parametrech závisí výsledná délka?

Řešení. Jednoduchým porovnáním vzorů je zřejmé, že délka výsledného vzoru je závislá na úhlu, pod kterým jsme vedli úsečky svírající jiný než pravý úhel s delší hranou. Mělo by to být zřejmé, protože to je jediné, v čem se vzory odlišují. Označme tento ostrý úhel \(\alpha\). Platí, že čím ostřejší je úhel \(\alpha\), tím větší je délka složeného vzoru. Čím blíže je tento úhel velikosti \(90^\circ\), tím je složený vzor kratší.

Zatím jsme porovnávali dva různé výsledky při obdobném dělení. Jak přesně ale závisí délka složeného vzoru na úhlu \(\alpha\) a na dalších parametrech? Při dalším zkoumání této závislosti je dobré zaměřit se na základní část vzoru.
Úloha 2. Jak závisí délka \(x\) základního vzoru Miura-ori ve složeném stavu na velikosti úhlu \(\alpha\) a délkách \(d\), \(l\)? Zadání viz obrázek.

Řešení. Je důležité označit parametry v obrázku na vhodných místech.

Pro \(\cos\alpha\) pak máme
\[ \cos\alpha = \frac{\frac{x}{2}}{d} = \frac{x}{2d},\]
odkud jednoduše vyjádříme
\[ x = 2d \cdot \cos\alpha.\]
Délka \(x\) tedy vůbec není závislá na \(l\), ale pouze na úhlu \(\alpha\) a délce \(d\).
Pojďme začít jednoduše a to proužkem papíru. Zkuste provést sklady na proužku papíru tak, aby se dal složit do roviny a současně abyste se po několika krocích s kratšími konci proužku papíru dostali k sobě (zatím stačí přiblžně). Současně nesmí dojít k překřížení delších okrajů proužku (dolní okraj musí zůstat dole, horní musí zůstat po celou dobu nahoře). Následující složení z obrázku by tedy nebylo řešením.

Několik možných řešení je na následujím obrázku.

Pokud proužky papíru opět rozvineme, uvidíme následující (viz obrázek).

Úloha 3. Pro předchozí typy řešení určete přesný vzor skladů proužku papíru tak, aby se oba konce potkaly přesně a šly slepit.
Řešení.
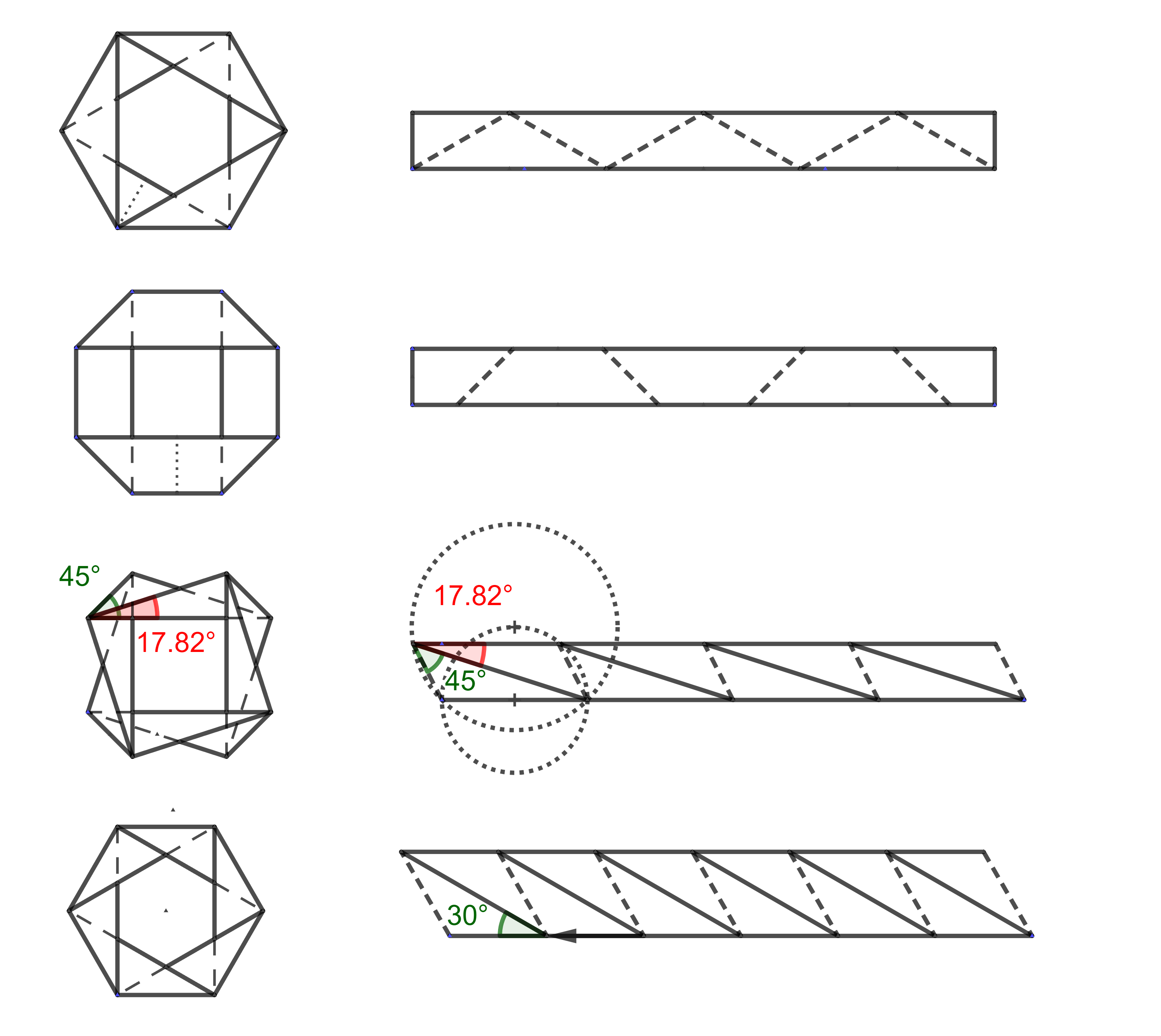
Jednotlivé proužky můžeme také skládat na sebe, pokud to uděláme vhodným způsobem, půjde vzor (po slepení proužku) opět složit do roviny. Ukázky viz obrázek
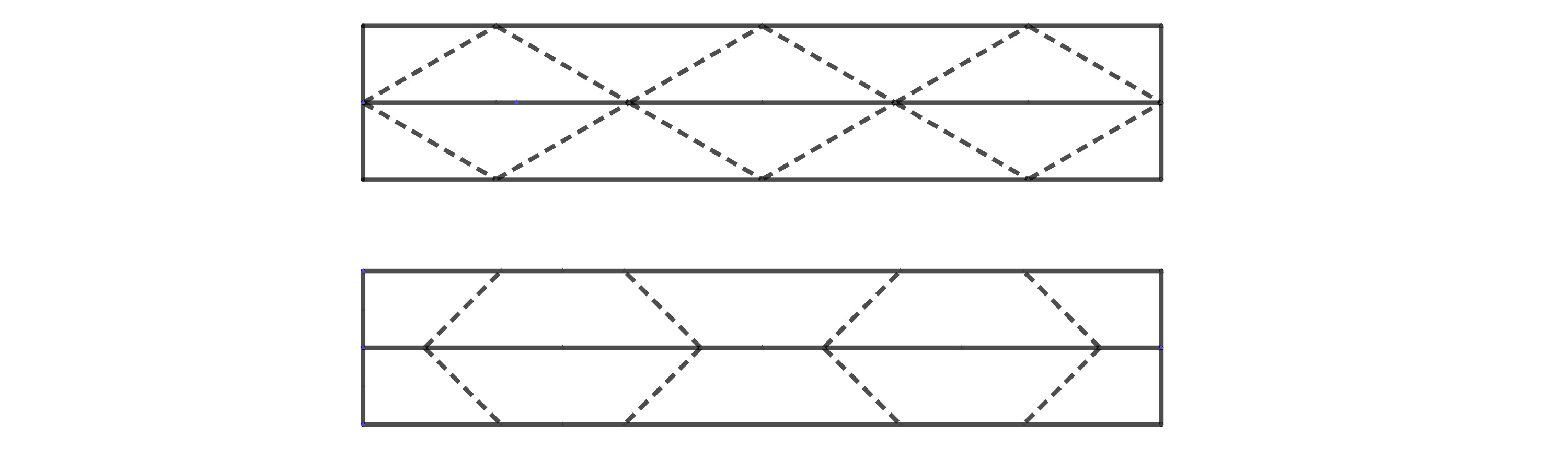
Literatura: https://www.youtube.com/watch?v=uFyJykl1O0k https://www.youtube.com/watch?v=ZVYz7g-qLjs https://laughingsquid.com/millidelta-small-origami-inspired-robot/ https://www.jpl.nasa.gov/news/solar-power-origami-style