diff --git a/00033_Cooling_Tower_Nuclear_Power_Station/en_article_proofreading.md b/00033_Cooling_Tower_Nuclear_Power_Station/en_article_proofreading.md
index 9a9a323..f06f46b 100644
--- a/00033_Cooling_Tower_Nuclear_Power_Station/en_article_proofreading.md
+++ b/00033_Cooling_Tower_Nuclear_Power_Station/en_article_proofreading.md
@@ -4,55 +4,51 @@ keywords:
- analytic geometry
- volume
- integral calculus
-is_finished: False
+is_finished: true
---
-# Volume of a nuclear power plant cooling tower
+# Volume of a Nuclear Power Plant Cooling Tower
The power plant's cooling towers are monumental structures made of concrete,
-towering towards the sky and emitting white clouds of water vapor.
+towering into the sky and emitting white clouds of water vapor.
These reinforced concrete shells, built on thin ten-meter legs,
are an integral part of the power plant's technology.
-Each cooling tower has a thermal output of over $1\,000\,\text{MW,}$,
-which means that every hour enough heat is released into the air to heat about eighty homes for 1 year.
+Each cooling tower has a thermal output of over $1{,}000\,\text{MW,}$.
+This means that every hour, enough heat is released into the air to heat about eighty homes for an entire year.
-The cooling tower of the Temelín nuclear power plant is in the shape of a one-piece rotating hyperboloid.
-From a height of twenty meters to the top at a height of $155\,\text{m}$, there is only empty space inside the tower.
-The thickness of this reinforced concrete shell is $90\,\text{cm}$ in the lower part of the tower,
-only three times greater than the thickness of the foundation slab of a family house.
+The cooling tower of the Temelín nuclear power plant is in the shape of a one-sheeted rotational hyperboloid.
+From a height of twenty meters up to the top at $155\,\text{m}$, the inside of the tower is completely hollow.
+This reinforced concrete shell is $90\,\text{cm}$ thick in the lower part of the tower,
+only three times thicker than a concrete foundation slab of a family house.
The thickness gradually decreases upwards and at the crown the shell is as wide as a car wheel (about $18\,\text{cm}$).
The entire shell is built on about a hundred concrete legs, forming air inlets.
-The circular pool beneath the tower, like the tower, has a diameter of approximately $130\,\text{m}$..
-
-nebo
-
-The circular pool below the tower (like the tower at the bottom) is approximately $130\,\text{m}$ in diameter.
+The circular pool beneath the tower (like the tower itself) has a diameter of approximately $130\,\text{m}$.

## Assignment
-Our task is to determine the volume of the cooling tower of the Temelín nuclear power plant. We will go about this task step by step. First, we will find a function to model the tower and then determine its volume using a definite integral.
+Our task is to determine the volume of the cooling tower of the Temelín nuclear power plant. We will go about this task step by step. First, we find a function to model the tower, and then we determine its volume using a definite integral.
-To simplify the calculations, we slightly idealize the real cooling tower (we round off some dimensions). We will assume that it has the shape of a part of a hyperboloid with a height of $155\,\text{m}$, a base radius of $65\,\text{m}$, and a crown radius of $41\,\text{m}$. Its narrowest point is $35\,\text{m}$ below the crown of the cooling tower.
+To simplify the calculations, we slightly idealize the real cooling tower (we round off some dimensions). Let's assume that the tower has the shape of a part of a hyperboloid of one sheet with a height of $155\,\text{m}$, a base radius of $65\,\text{m}$, and a crown radius of $41\,\text{m}$. Its narrowest point is $35\,\text{m}$ below the crown of the cooling tower.
-In order to work in coordinates, as we are used to, we will place the axis of the rotating hyperboloid so that it coincides with the coordinate axis $x$. Moreover, we place it so that the section of the cooling tower along its axis is a part of the hyperbola on which the base of the tower with coordinates $[155, 65]$ and the top of the crown lie $[0, 41]$. Since the narrowest point of the tower is $35\,\text{m}$ below the crown of the cooling tower, the center of the hyperbola has coordinates $[35, 0]$. The cooling tower is created by rotating a part of this hyperbola around the $x$ axis.
+In order to work with coordinates, as we are used to, we will place the axis of the rotational hyperboloid so that it coincides with the coordinate axis $x$. Moreover, we place it so that the cross-section of the cooling tower along its axis forms a part of a hyperbola, with the base of the tower located at the point $[155, 65]$ and the top (the crown) at $[0, 41]$. Since the narrowest part of the tower is $35\,\text{m}$ below the crown of the cooling tower, the center of the hyperbola has coordinates $[35, 0]$. The cooling tower can be created by rotating a part of this hyperbola around the $x$-axis.
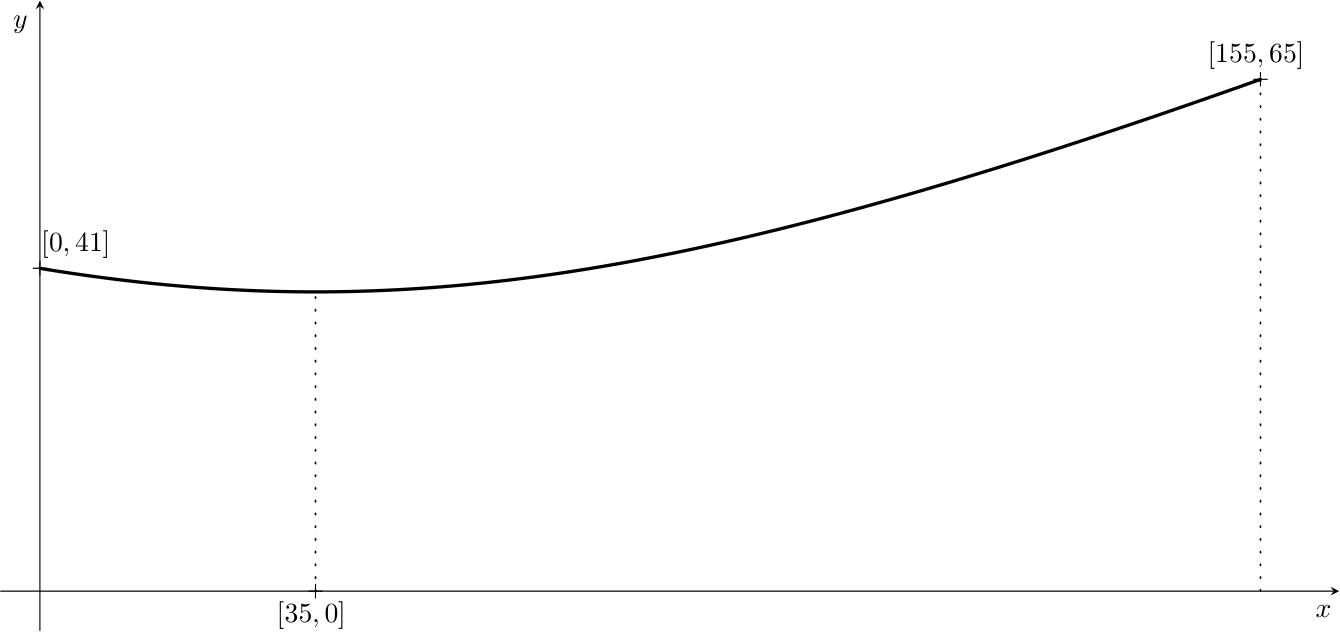
-> **Exercise 1.** Write the general equation of a hyperbola with center $[35, 0]$ and foci lying on an axis parallel to the $x$ axis.
+> **Exercise 1.** Write the standard form of the equation of a hyperbola with center $[35, 0]$ and foci lying on an axis parallel to the $x$-axis.
\iffalse
-*Solution.* The general equation of a hyperbola has the form
+*Solution.* The standard form of the equation of a hyperbola is
$$\frac{y^2}{a^2} - \frac{(x - 35)^2}{b^2} = 1.$$
\fi
-> **Exercise 2.** Determine the general equation of the hyperbola,
-> of which the section of the cooling tower is a part, if the points $[155, 65]$ and $[0, 41]$ lie on it.
-> Substitute the values rounded to units for $a^2$, $b^2$ in the equation.
+> **Exercise 2.** Determine the standard form of the equation of the hyperbola,
+> that the section of the colling tower is a part of, given that points $[155, 65]$ and $[0, 41]$ lie on it.
+> Substitute the values rounded to the nearest whole number for $a^2$, $b^2$ in the equation.
\iffalse
@@ -67,41 +63,41 @@ Expressing $\frac{1}{a^2}$ from the first equation
$$\frac{1}{a^2}=\frac{1}{65^2}\left(1+\frac{120^2}{b^2}\right)$$
and substituting it into the second equation, we obtain
$$\frac{41^2}{65^2}\left(1+\frac{120^2}{b^2}\right)-\frac{35^2}{b^2} = 1.$$
-Now we calculatee $b^2$:
-$$b^2 = \frac{41^2 \cdot 120^2 - 35^2 \cdot 65^2}{65^2-41^2} \;\dot{=}\; 7481.$$
+Now we solve for $b^2$:
+$$b^2 = \frac{41^2 \cdot 120^2 - 35^2 \cdot 65^2}{65^2-41^2} \;\dot{=}\; 7{,}481.$$
After substituting back, we get
-$$a^2= \frac{41^2 \cdot 120^2 - 35^2 \cdot 65^2}{120^2-35^2} \;\dot{=}\; 1444.$$
-The hyperbola modeling the section of a cooling tower has the general equation
-$$\frac{y^2}{1444} - \frac{(x - 35)^2}{7481} = 1.$$
+$$a^2= \frac{41^2 \cdot 120^2 - 35^2 \cdot 65^2}{120^2-35^2} \;\dot{=}\; 1{,}444.$$
+The hyperbola modeling the section of a cooling tower has the standard form of the equation
+$$\frac{y^2}{1{,}444} - \frac{(x - 35)^2}{7{,}481} = 1.$$
\fi
-> **Exercise 3.** From the general hyperbola equation,
+> **Exercise 3.** From the standard form of the equation of the hyperbola,
> express the function that describes the branch of the hyperbola lying above the $x$-axis.
\iffalse
-*Solution.* From the general equation of the hyperbola
-$$\frac{y^2}{1444} - \frac{(x - 35)^2}{7481} = 1$$
+*Solution.* From the standard form of the equation of the hyperbola
+$$\frac{y^2}{1{,}444} - \frac{(x - 35)^2}{7{,}481} = 1$$
we express $y$
-$$y(x) = \pm\sqrt{1444 + \frac{1444}{7481} (x - 35)^2}.$$
+$$y(x) = \pm\sqrt{1{,}444 + \frac{1{,}444}{7{,}481} (x - 35)^2}.$$
The branch of the hyperbola lying above the $x$-axis is described by the function
-$$y(x) = \sqrt{1444 + \frac{1444}{7481} (x - 35)^2}.$$
+$$y(x) = \sqrt{1{,}444 + \frac{1{,}444}{7{,}481} (x - 35)^2}.$$
\fi
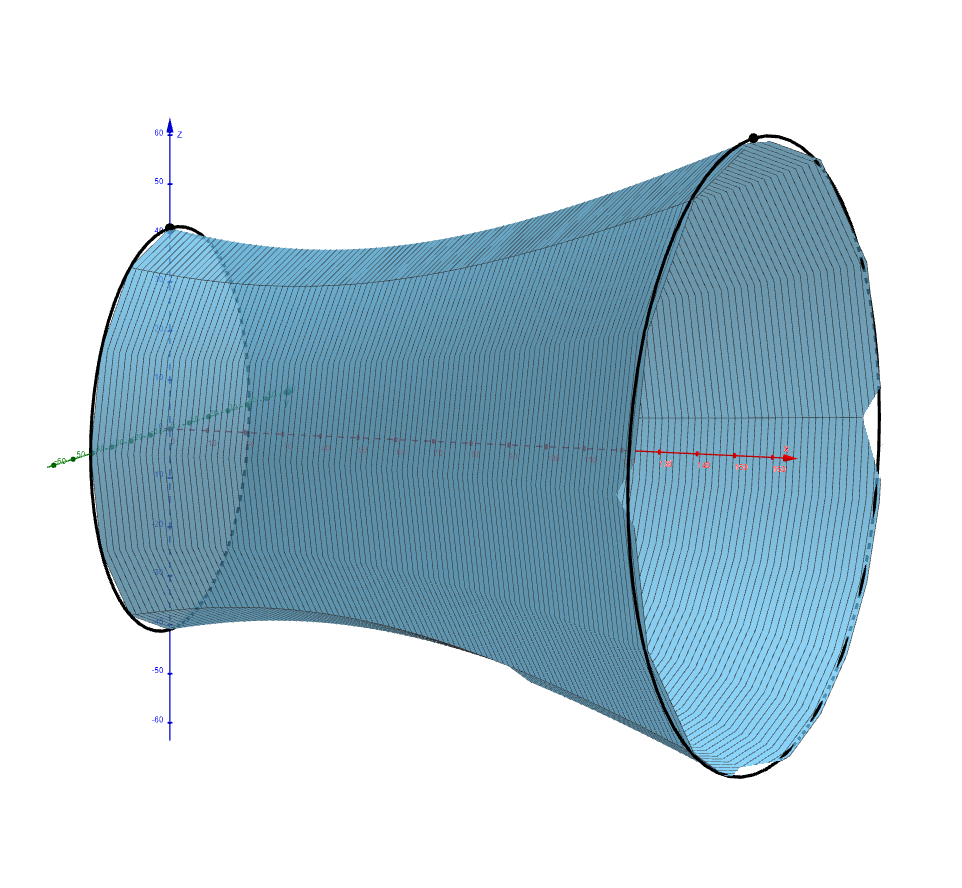
-> **Exercise 4.** Calculate the volume of the solid of revolution formed by rotating a part of the arm of the hyperbola modeling the cooling tower in the interval
+> **Exercise 4.** Calculate the volume of the solid of revolution formed by rotating a part of the branch of the hyperbola modeling the cooling tower on the interval
> $x\in\langle 0, 155\rangle$ around the $x$-axis.
\iffalse
-*Solution.* To calculate the volume, we use a definite integral expressing the volume of a rotating body
-$$V = \pi \int_{0}^{155} \left(1444 + \frac{1444}{7481} (x - 35)^2\right) \,\mathrm{d}x= \pi \left[1444x + \frac{1444}{7481} \cdot \frac{1}{3}(x - 35)^3 \right]_{0}^{155}\doteq1\,052\,436\,\text{m}^3$$
-The volume of the model of the cooling tower of the Temelín nuclear power plant is $1\,052\,436\,\text{m}^3$.
+*Solution.* To calculate the volume, we use a definite integral expressing the volume of a solid of revolution
+$$V = \pi \int_{0}^{155} \left(1{,}444 + \frac{1{,}444}{7{,}481} (x - 35)^2\right) \,\mathrm{d}x= \pi \left[1{,}444x + \frac{1{,}444}{7{,}481} \cdot \frac{1}{3}(x - 35)^3 \right]_{0}^{155}\doteq1{,}052{,}436\,\text{m}^3$$
+The volume of the model of the cooling tower of the Temelín nuclear power plant is $1{,}052{,}436\,\text{m}^3$.
-*Note.* If we compare the obtained volume of $1\,052\,436\,\text{m}^3$ of the cooling tower model with the volume of $1\,069\,700\,\text{m}^3$
+*Note.* If we compare the obtained volume of $1{,}052{,}436\,\text{m}^3$ of the cooling tower model with the volume of $1{,}069{,}700\,\text{m}^3$
of the real cooling tower in Temelín, we see that our result is quite realistic.
\fi