diff --git a/00030_Ecosystems_on_Island/en_article_proofreading.md b/00030_Ecosystems_on_Island/en_article_proofreading.md
index 9a983f3..22ca4b5 100644
--- a/00030_Ecosystems_on_Island/en_article_proofreading.md
+++ b/00030_Ecosystems_on_Island/en_article_proofreading.md
@@ -27,7 +27,7 @@ In the following problems, we will solve tasks related to formula (1) and show h
## Exercises
-> **Exercise 1:** Take the logarithm of both sides of equation (1). Show that the resulting dependence is linear, i.e., the graph of the logarithm of the area as a function of the logarithm of species number is a straight line.
+> **Exercise 1:** Take the logarithm of both sides of equation (1). Show that the resulting dependence is linear, i.e., if the logarithm of the area size is plotted as a function of the logarithm of the number of species the graph of this dependence is a straight line.
*Solution.* We start with relationship (1), i.e., $$N=c A^k.$$
@@ -35,7 +35,7 @@ Taking the logarithm we get
$$\log N= \log (c A^k).$$
-Using the rules for the logarithm of a product and the logarithm of a power function we obtain
+Using the rules for logarithms of products and powers, we obtain
$$\log N= \log (c) + k\log A.$$
@@ -45,13 +45,13 @@ $$y=kx+q,$$
which is the equation of a line with slope $k$.
-**Note:** Since it is not always convenient to calculate two logarithms for each value when plotting, logarithmic axes are used. The distance of point $x$ from point 1 is $\log x$, and this scale is used for both the horizontal and vertical axes.
+**Note:** Since it is not always convenient to calculate two logarithms for each value when plotting, logarithmic axes are used. The distance of a point $x$ from the point 1 on a logarithmic axis is $\log x$, and this scale is used for both the horizontal and vertical axes.
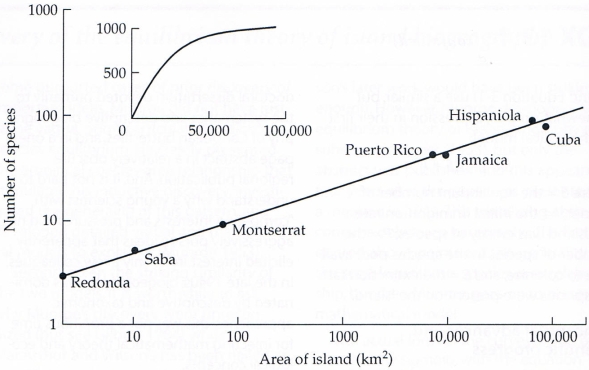
-The attached image shows that the graph of a power function in logarithmic axes is a straight line. The graph includes the number of reptile and amphibian species on islands in the West Indies (Antilles and Bahamas). In a graph with logarithmic axes, the data align almost exactly in a straight line. This property is easily detectable both optically from the data and through mathematical methods. The smaller picture shows how the dependence would look without using logarithmic axes. The data form an arc of a curve and it is not immediately clear whether it is a power curve, an exponential curve, or some other dependence.
+The attached image shows that the graph of a power function in logarithmic axes is a straight line. The graph includes the number of reptile and amphibian species on islands in the West Indies (Antilles and Bahamas). In a graph with logarithmic axes, the data align almost exactly in a straight line. This property is easily visible in the data and can also be easily confirmed through mathematical methods. The smaller picture shows how the dependence would look without using logarithmic axes. The data lie along a curve, and it is not immediately clear whether it is a power curve, an exponential curve, or some other dependence.
-> **Exercise 2:** It is estimated that for a certain area, the value of the exponent $k$ is $0.15$. How will the number of species decrease if the area is reduced to one-tenth? (This exercise models extensive forest logging.)
+> **Exercise 2:** It is estimated that for a certain area, the value of the exponent $k$ is $0.15$. By how much will the number of species decrease if the area is reduced to one-tenth? (This exercise models, for example, extensive forest logging.)
*Solution.* Starting from the law $$N(A)=c A^k$$ and reducing the area to one-tenth, we get
$$N(0.1A) = c\cdot(0.1 A)^k = c A^k \cdot 0.1^k = N(A)\cdot 0.1^k$$
@@ -67,10 +67,10 @@ and
$$N_2 = c A_2^k.$$
By dividing these equations, we get
$$\frac{N_1}{N_2} = \frac{c A_1^k}{ c A_2 ^k} =\left(\frac {A_1}{A_2}\right)^k.$$
-According to the problem, $N_2=0.7N_1$ and $A_2=0.25A_1$, i.e.,
+According to the stated problem, $N_2=0.7N_1$ and $A_2=0.25A_1$, i.e.,
$$\frac{N_1}{0.7N_1}=\left(\frac{A_1}{0.25A_1}\right)^k$$
$$\frac{1}{0.7}=\left(\frac{1}{0.25}\right)^k.$$
-Taking logarithms, we obtain
+Taking the logarithm of both sides, we obtain
$$\log\frac{1}{0.7}=k\cdot\log\frac{1}{0.25}.$$
and thus
$$k=\frac{\log \frac1{0.7}}{\log 4}\approx 0.257.$$