diff --git a/00027_Golden_Ratio/en_article_proofreading.md b/00027_Golden_Ratio/en_article_proofreading.md
index bec134d..ffbd237 100644
--- a/00027_Golden_Ratio/en_article_proofreading.md
+++ b/00027_Golden_Ratio/en_article_proofreading.md
@@ -1,37 +1,36 @@
---
keywords:
-- planimetry
+- plane geometry
- chain fraction
- quadratic equation
-is_finished: False
+is_finished: true
---
-# Golden Section and Chain Fraction
+# The Golden Ratio and Continued Fractions
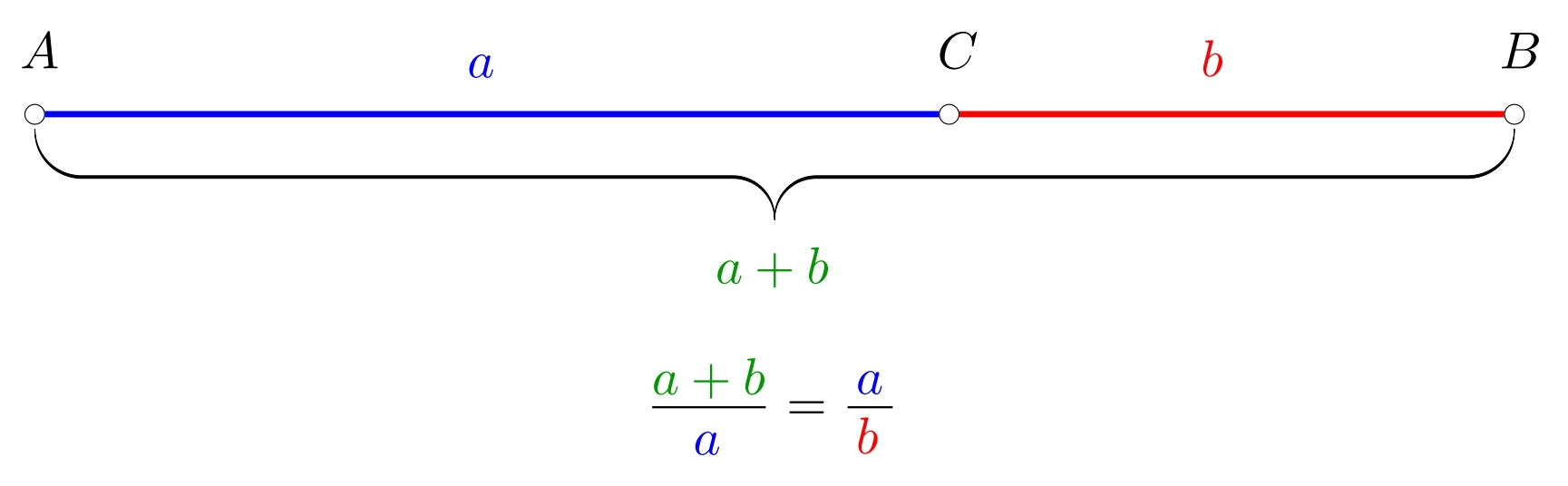
-Let us have a segment $AB$ and a point $C$ on it. We say that the point $C$
-divides the line segment $AB$ in the ratio of the golden section,
-if the relation $$\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}$$
-applies to the lengths of the considered segments.
+Let us have a line segment $AB$ and a point $C$ that lies on it. We say that point $C$
+divides line segment $AB$ in the golden ratio,
+if the lengths of the segments satisfy equation $$\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}.$$
This ratio is often denoted by the Greek letter $\varphi$
-and has a value of approximately $1{,}618$.
+and has a value of approximately $1{.}618$.
A nice example of the use of the golden ratio in everyday life is the credit card.
-It has the shape of a so-called golden rectangle, the sides of which meet the golden ratio.
+It has the shape of a so-called golden rectangle, the sides of which satisfy the golden ratio.
The golden rectangle is a popular shape because of its balanced appearance;
it is neither too long nor too wide.
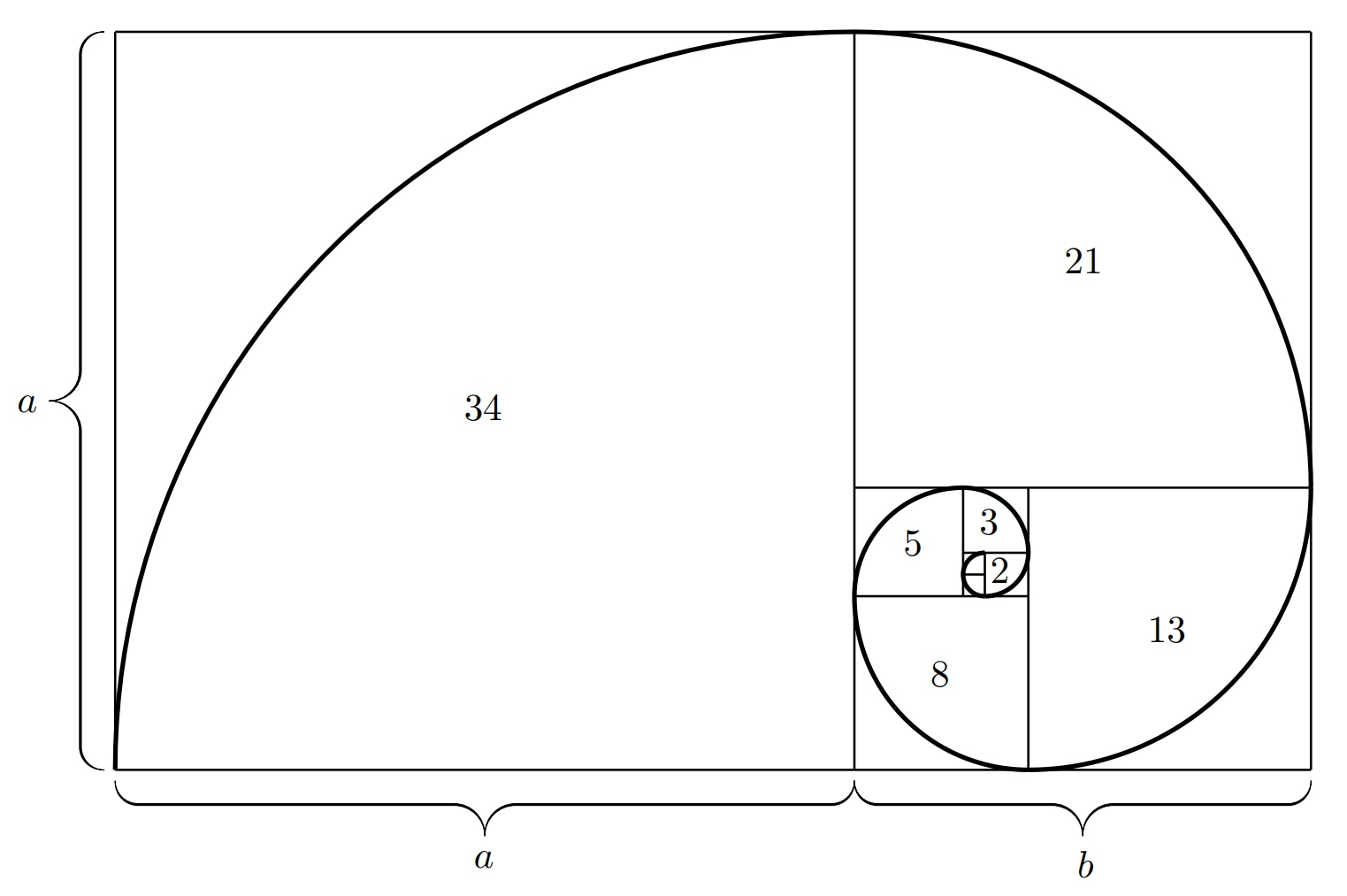
The golden ratio is closely related to the Fibonacci sequence.
-The members of the Fibonacci sequence are the numbers
-$1$, $1$, $2$, $3$, $5$, $8$, $13$, $21$, $34$, $55$, ..., where each
-next member of the sequence is obtained by the sum of the previous two members.
-We also refer to the individual elements of this sequence as Fibonacci numbers.
-What is the connection between the Fibonacci sequence and the golden section?
-It is true that the limit of the ratios of two consecutive members
-of this sequence is exactly equal to the golden section $\varphi$.
+The terms of the Fibonacci sequence are numbers
+$1$, $1$, $2$, $3$, $5$, $8$, $13$, $21$, $34$, $55$, ..., where each term
+is the sum of the two preceding ones.
+We also refer to the individual terms of this sequence as Fibonacci numbers.
+What is the connection between the Fibonacci sequence and the golden ratio?
+It holds that the limit of the ratio of two consecutive terms
+of this sequence equals the golden ratio $\varphi$.
If we construct squares whose side lengths correspond exactly to the Fibonacci numbers,
it is possible to arrange them nicely next to each other
@@ -43,74 +42,74 @@ In nature, the golden ratio appears in the form of the Fibonacci sequence.
We can find it in the arrangement of the leaves on the stems.
The leaves grow one above the other so that they do not shade each other,
the transition from one leaf to the next has the character
-of a helical ascent around the stem.
+of a spiral growth around the stem.
Similar arrangements are found in the scales of the pine cone,
the seeds of the sunflower, or the the pineapple peel.
-The logarithmic spiral is also found in the shells of molluscs or in the
+The logarithmic spiral is also found in the mollusc shells or in the
fiddlehead fern. Tornadoes, cyclones and galaxies also have this shape.
-The golden section is widely used in art to achieve aesthetically impressive
+The golden ratio is widely used in art to achieve aesthetically impressive
and harmonious compositions. Painters and photographers use this ratio
to determine the placement of key elements in their works.
-Architects often integrate the golden section into building designs.
+Architects often integrate the golden ratio into building designs.
-## An infinite chain fraction/Continued fraction
+## Infinite Continued Fraction
-An infinite chain fraction (also called continued fraction) is an expression of the form
+An infinite continued fraction is an expression of the form
$$x = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \ddots}}},$$
-where $a_0$ is an integer and the numbers $a_i$ are positive natural numbers for $i\in\mathbb{N}$. A chain fraction can also be in finite form.
+where $a_0$ is an integer and the numbers $a_i$ are positive natural numbers for $i\in\mathbb{N}$. A continued fraction can also be finite.
-The golden section can be expressed by the continued fraction
+The golden ratio can be expressed by the continued fraction
$$\varphi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}.$$
> **Exercise 1.**
-> Calculate approximate values of the golden section using finite chain fractions
+> Calculate approximate values of the golden ratio using finite continued fractions
>
> 1. $$1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1}}}$$
> 2. $$1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1}}}}$$
*Solution.*
-1. $$1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1}}}= 1 + \cfrac{1}{1 + \cfrac{1}{2}}= 1 + \cfrac{1}{\frac{3}{2}}=\frac{5}{3}\doteq1{,}67$$
-2. $$1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1}}}}=1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{2}}}=1 + \cfrac{1}{1 + \cfrac{1}{\frac{3}{2}}}=1 + \cfrac{1}{\frac{5}{3}}=\frac{8}{5}=1{,}6$$
+1. $$1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1}}}= 1 + \cfrac{1}{1 + \cfrac{1}{2}}= 1 + \cfrac{1}{\frac{3}{2}}=\frac{5}{3}\doteq1{.}67$$
+2. $$1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1}}}}=1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{2}}}=1 + \cfrac{1}{1 + \cfrac{1}{\frac{3}{2}}}=1 + \cfrac{1}{\frac{5}{3}}=\frac{8}{5}=1{.}6$$
> **Exercise 2.**
> Calculate the exact value of the golden ratio $\varphi$.
*Solution.*
-Assume that line segment $AB$ has length $1$. We divide this segment
-by the point $C$ in the ratio of the golden section. Then it holds
+Let's assume that line segment $AB$ has length $1$. We divide this line segment
+by the point $C$ in the golden ratio. Then we have
$$\varphi=\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}.$$ Let's denote
-$x=|AC|$, i.e. $x$ will be the length of the longer segment of the segment $AB$.
+$x=|AC|$, i.e. $x$ is the length of the longer line segment of the line segment $AB$.
Then $|BC|=1-x$ holds for the length of the line segment $BC$
-and thus we obtain the relation
+and thus we obtain the equation
$$\frac{1}{x} = \frac{x}{1-x},\tag{1}$$
-which makes sense for $x\neq0 \text{ a } x\neq1$.
-However, we do not need to investigate these extreme values,
-because they certainly do not meet the golden ratio.
-By adjusting (1), we get a quadratic equation
+which is defined for $x\neq0 \text{ and } x\neq1$.
+However, we do not need to consider these extreme values,
+because they certainly do not correcpond to the golden ratio.
+By manipulating (1), we obtain a quadratic equation
$$x^2 + x - 1 = 0,$$
whose roots are
$$x_{1,2} = \frac{-1 \pm \sqrt{5}}{2}.$$
-In our case, $x$ is the length of the line segment; therefore, a negative value of $x$ is meaningless.
+In our case, $x$ is the length of the line segment; therefore, a negative value of $x$ is not valid.
Thus, we have the only satisfying solution to equation (1)
$$x_1 = \frac{-1 + \sqrt{5}}{2}.$$
Now we can calculate the value of the golden section $\varphi$:
$$\varphi=\frac{|AB|}{|AC|}=\frac{1}{x} = \frac{1}{\frac{-1 + \sqrt{5}}{2}}=\frac{2}{\sqrt{5}-1}.$$
By rationalizing the denominator we then get
-$$\varphi=\frac{\sqrt{5}+1}{2}\doteq1{,}618.$$
+$$\varphi=\frac{\sqrt{5}+1}{2}\doteq1{.}618.$$
> **Exercise 3.**
-> Solve an equation inspired by the golden ratio in a finite chain fraction
+> Solve an equation inspired by the golden ratio in a finite continued fraction
> $$ x = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{x}}}. $$
*Solution.*
-First, we simplify the equation step by step.
+Let's simplify the equation step by step.
$$
\begin{aligned}
-x &= 1 + \cfrac{1}{1 + \cfrac{1}{\frac{x+1}{x}}}\qquad\text{pro }x\neq0\\
-x &= 1 + \cfrac{1}{1 + \cfrac{x}{x+1}}\qquad\text{pro }x\neq-1\\
+x &= 1 + \cfrac{1}{1 + \cfrac{1}{\frac{x+1}{x}}}\qquad\text{for }x\neq0\\
+x &= 1 + \cfrac{1}{1 + \cfrac{x}{x+1}}\qquad\text{for }x\neq-1\\
x &= 1 + \cfrac{1}{\frac{x+1+x}{x+1}}\\
x &= 1 + \frac{x+1}{2x+1}\\
x &= \frac{3x+2}{2x+1}\\
@@ -118,11 +117,11 @@ x &= \frac{3x+2}{2x+1}\\
$$
-Under the condition $x\neq -\frac12$ we obtain a quadratic equation from here
+Under the condition $x\neq -\frac12$ we obtain a quadratic equation
$$2x^2 - 2x - 2 = 0.$$
-Her roots are
+Its roots are
$$x_{1,2} = \frac{1 \pm \sqrt{5}}{2}.$$
-Note that one of the solutions is again a value of the golden section.
+Note that one of the solutions is again the golden ratio.
## Literature