diff --git a/00026_Logic_circuits/en_article_proofreading.md b/00026_Logic_circuits/en_article_proofreading.md
index f3a2d80..8bd0e5d 100644
--- a/00026_Logic_circuits/en_article_proofreading.md
+++ b/00026_Logic_circuits/en_article_proofreading.md
@@ -2,13 +2,13 @@
keywords:
- statements
- mathematical logic
-is_finished: False
+is_finished: True
---
-# Logic circuits
+# Logic Circuits
Which spell can turn on the correct indicator light in an overloaded elevator,
-prepare an orange soda by pressing the button of a vending machine,
+prepare an orange soda by pressing the button on a vending machine,
turn off the lights in the hallway of a house after a few minutes,
or move a character on a computer screen?
These and many other real-life activities are handled by logic circuits,
@@ -29,7 +29,7 @@ Low voltage indicates a truth value of 0, while a high voltage level indicates a
For example, if the AND gate has a low voltage level at input A and
a high voltage level at input B, the output is a low voltage level.
The specific values of the levels vary according to the specific use of the circuit.
-A low level of approximately 0V and a high level of approximately 5V are common.
+A low level of approximately 0 V and a high level of approximately 5 V are common.
In the next figure we see a representation of a more complex logic circuit.
For clarity, the figure also shows the sequential compounding of statements,
@@ -42,8 +42,8 @@ Thus, the output of one gate can be fed to multiple inputs at the same time.
In the following exercises, switches or buttons can be placed in front of the inputs,
and light bulbs can be placed behind the outputs of the logic circuit.
Let's agree that the logic value at the input is equal to 1
-exactly when the switch is on or the button is pressed.
-Similarly, a light bulb lights up only when there is a logic 1 at the corresponding output.
+if and only if the switch is on or the button is pressed.
+Similarly, a light bulb lights if and only if there is a logic value of 1 at the corresponding output.
> **Exercise 1.** In the circuit in the previous figure, there are switches
> in front of inputs A, B and C, and a light bulb is connected to the output.
@@ -54,22 +54,22 @@ Similarly, a light bulb lights up only when there is a logic 1 at the correspond
We know from the assignment that $p(\mathrm{C})=0$, and we ask for the values of
$p(\mathrm{A})$ and $p(\mathrm{B})$ such that
$p\left[ \left(\mathrm{C}\wedge \left(\mathrm{A}\vee\mathrm{B}\right)\right)\vee \left( \neg\left(\mathrm{A}\vee\mathrm{B}\right)\right) \right]=1$.
-We will solve the exercise with reasoning.
+We will solve the exercise by reasoning.
If $p(\mathrm{C})=0$ holds, then necessarily
$p(\mathrm{C}\wedge \left(\mathrm{A}\vee\mathrm{B}\right))=0$. Therefore the statement
$\neg ( \mathrm{A}\vee \mathrm{B})$ must be true, and therefore $p(\mathrm{A}\vee \mathrm{B})=0$.
However, this is possible if and only if the statements $\mathrm{A}$ and
-$\mathrm{B}$ are both false. Thus, neither switch may be turned on.
+$\mathrm{B}$ are both false. Therefore, both switches must remain closed.
> **Exercise 2.** The logic circuit shown in the figure below is given with switches at inputs A, B and C
-> and a light bulb at output Z. Which switches must be turned on for the bulb to light up?
+> and a light bulb at output Z. Which switches must be turned on for the bulb to light?
> Find all solutions to the problem. If the wires cross in the diagram without a node shown,
> it is assumed that there is no actual contact between the wires.
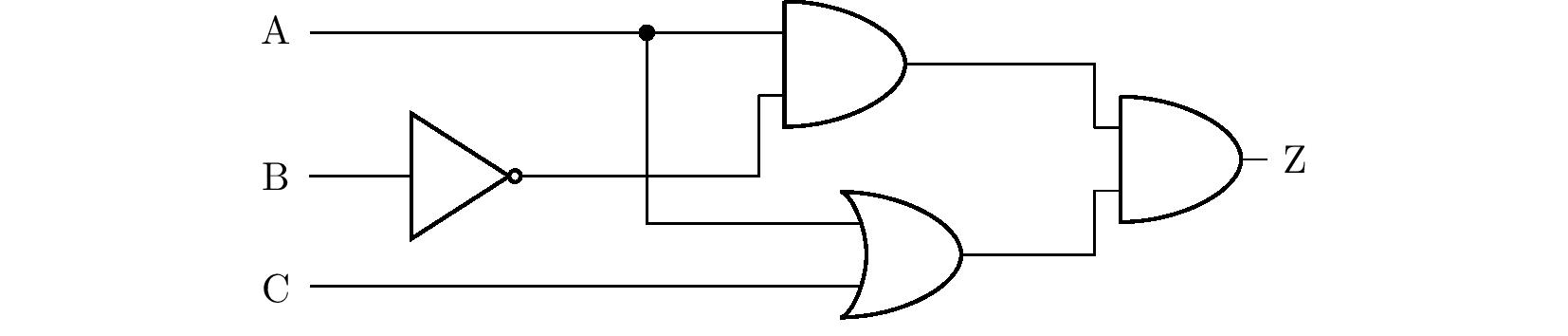
-*Solution.* We will solve the problem by using the truth value table.
+*Solution.* We will solve the problem by using the truth table.
From the diagram in the assignment, we first derive a statement
consisting of the statements $\mathrm{A}$, $\mathrm{B}$ and $\mathrm{C}$,
which will be equivalent to the statement $\mathrm{Z}$, see figure.
@@ -89,12 +89,12 @@ For the compound statement $\left( \star \right)$ we now create a truth table:
| $0$| $0$| $1$ | $\quad0$ | $\quad1$ | $\qquad\qquad0$ |
| $0$| $0$| $0$ | $\quad0$ | $\quad0$ | $\qquad\qquad0$ |
-The table shows that the light bulb will light up if switch
+The table shows that the bulb lights if switch
A is closed and switch B is not closed at the same time.
-Switch C does not matter.
+The position of switch C does not matter.
The problem can also be solved by equivalent modifications of the statement
-$\left(\star \right)$. First, we use the distributive law, then the so-called idempotency law
+$\left(\star \right)$. First, we use the distributive law, then the so-called idempotent law
$\mathrm{A}\wedge \mathrm{A}\Leftrightarrow \mathrm{A}$:
$$
@@ -135,15 +135,15 @@ which corresponds to the diagram of the resulting circuit in the figure:
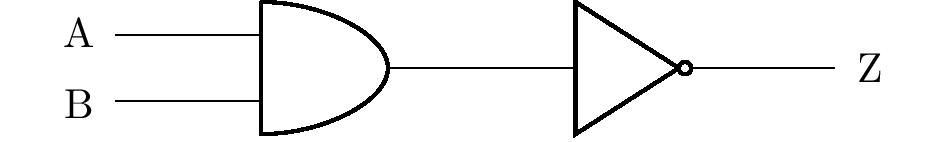
-The problem has more solutions. For example, using de Morgan's Morgan's law,
+The problem has more solutions. For example, using de Morgan's laws,
we get from the previous result the equivalent statement $\neg\mathrm{A}\vee\neg\mathrm{B}$.
-A different, but also correct, circuit (diagram) would correspond to this statement.
+This statement could be represented by a different, but equally correct, circuit diagram.
> **Exercise 4.** Modify the warning device from the previous exercise.
> Red and green lights will now be connected to the two outputs.
-> If both pumps are working, the green light is on and the red light is off.
-> If one of the pumps fails, the red light will also light up, and if both pumps fail,
-> only the red light will light up. Design the corresponding logic circuit.
+> If both pumps work, the green light is on and the red light is off.
+> If one of the pumps fails, the red light also lights up, and if both pumps fail,
+> only the red light lights up. Design the corresponding logic circuit.
*Solution.* Similar to the previous problem, let us denote by $\mathrm{A}$
and $\mathrm{B}$ the statements representing the state of the first and second pumps.
@@ -158,7 +158,7 @@ $\mathrm{R}$ (red light) and $\mathrm{G}$ (green light):
| $0$|$0$|$1$|$0$|
We can see that the column for the statement $\mathrm{R}$ is identical to the
-statement $\mathrm{G}$ in the previous exercise (and thus we can adopt its solution),
+statement $\mathrm{Z}$ in the previous exercise (and thus we can adopt its solution),
and the column for the statement $\mathrm{G}$ corresponds to the disjunction
$\mathrm{A}\vee \mathrm{B}$. By using nodes and branching the circuit,
we can draw a diagram of the corresponding logic circuit:
@@ -170,13 +170,13 @@ the correctness of which can always be verified using the truth table.
However, we will discuss one of the solutions in more detail.
Students may think that instead of an OR gate, the wires
-can be connected with a simple knot as shown in the figure:
+can be connected with a simple node as shown in the figure:
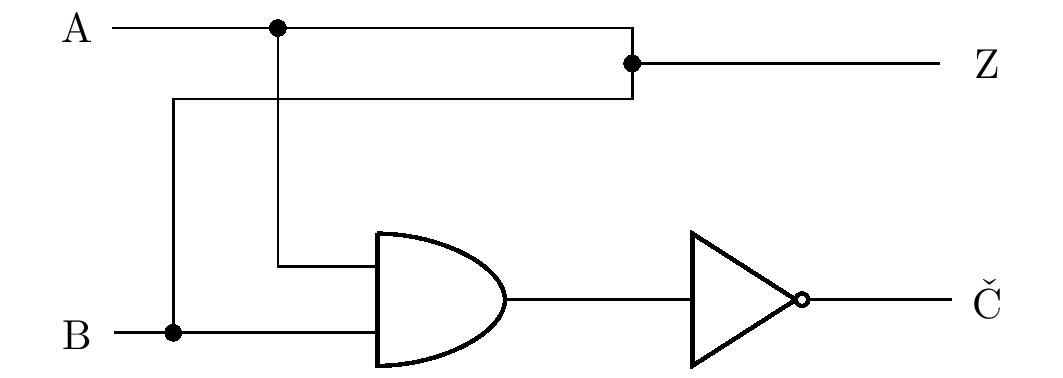
If there is a value of $1$ on $\mathrm{A}$ or $\mathrm{B}$ (or both),
can this value flow freely to the output $\mathrm{G}\,$?
-The reality is that it doesn't. In the opening paragraph,
+The reality is that it can't. In the opening paragraph,
we noted that the truth value $1$ is realized by a high voltage level and the value $0$ by its low level.
Thus, for example, if there is a high voltage at the input $\mathrm{A}$
and a low voltage at the input $\mathrm{B}$, a short circuit will occur in the circuit,
@@ -184,7 +184,7 @@ because points with different voltages are connected by a wire.
Therefore, in general, we cannot connect the outputs of different gates by nodes in logic circuits.
> **Exercise 5.** Design a two-input, one-output logic circuit
-> that simulates a logical equivalence operation.
+> that performs logical equivalence.
*Solution.* In order to construct the circuit, we need to find a
compound statement equivalent to $\mathrm{A}\Leftrightarrow\mathrm{B}$
@@ -205,20 +205,20 @@ and negations. We can therefore construct the corresponding diagram:
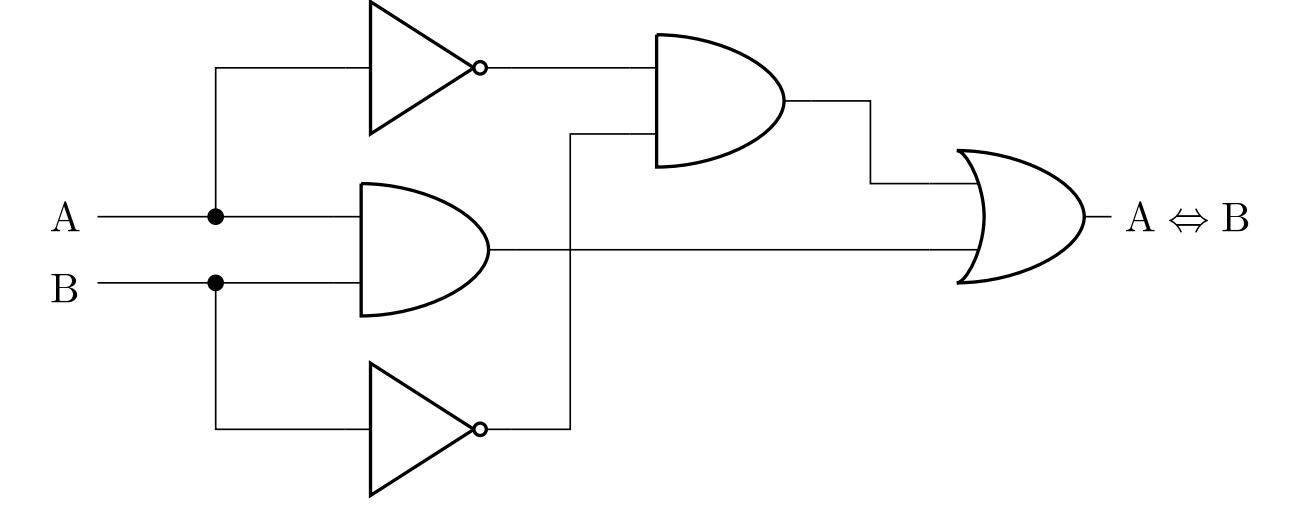
One of the other possible solutions can be obtained by using de Morgan's laws
-and by equivalent modifications of the previous result to the statement
+and by equivalent modifications of the previous result to statement
$\left( \mathrm{A}\wedge\mathrm{B} \right) \vee \neg \left( \mathrm{A}\vee\mathrm{B} \right)$.
-The technical advantage of this form is the smaller number of necessary logic elements
+The technical advantage of this form is the smaller number of necessary logic gates
when implementing the circuit.
> **Exercise 6.** After pressing the appropriate button,
> the coffee machine can prepare three types of drinks: lungo, macchiato and cocoa.
-> Drinks are prepared by mixing four ingredients (hot water, milk, coffee and cocoa concentrate),
-> where each ingredient has its own nozzle. Design a logic circuit with three inputs
+> Drinks are prepared by mixing four ingredients (hot water, milk, coffee and cocoa concentrate).
+> Each ingredient has its own nozzle. Design a logic circuit with three inputs
> (one for each drink) and four outputs (one for each nozzle valve)
-> if lungo is prepared from water and coffee concentrate, macchiato from water,
+> given that lungo is prepared from water and coffee concentrate, macchiato from water,
> milk and coffee concentrate, and cocoa from water and cocoa concentrate.
>
-> For the sake of simplicity, let's assume that no one thinks of pressing multiple buttons at once,
+> For the sake of simplicity, let's assume that no one thinks of pressing multiple buttons at the same time,
> so you don't need to deal with these cases. The ingredient is released into the cup
> exactly when there is a logic one at the corresponding output.
@@ -227,7 +227,7 @@ and $\mathrm{M}$ (macchiato) statements representing the state of pressing the c
and further denote $\mathrm{COC}$ (cocoa concentrate), $\mathrm{WA}$ (water),
$\mathrm{COF}$ (coffee concentrate) and $\mathrm{ML}$ (milk)
statements representing the opening status of the respective nozzle.
-From the information in the assignment, let's compile a table of truth values:
+From the information in the assignment, let's create a truth table:
| $\mathrm{C}$ |$\mathrm{L}$| $\mathrm{M}$ | $\mathrm{COC}$ | $\mathrm{WA}$ | $\mathrm{COF}$ | $\mathrm{ML}$|
|--|--|--|---|---|---|---|
@@ -236,10 +236,10 @@ From the information in the assignment, let's compile a table of truth values:
|$0$ |$0$ |$1$ |$0$ |$1$ |$1$ |$1$|
|$0$ |$0$ |$0$ |$0$ |$0$ |$0$ |$0$|
-Rows for which there is more than one 1 in the first three columns are not taken into account,
+Rows with more than one 1 in the first three columns are not taken into account,
since only one button can be pressed at a time.
-It follows from the table that the equivalent pair of statements is $\mathrm{COC}$
+The table shows that the equivalent pair of statements is $\mathrm{COC}$
and $\mathrm{C}$ and another equivalent pair is the statements $\mathrm{ML}$ and $\mathrm{M}$.
The statement $\mathrm{COF}$ is true if and only if one of the statements $\mathrm{L}$
or $\mathrm{M}$ is true, i.e. it is equivalent to the disjunction $\mathrm{L}\vee\mathrm {M}$.
@@ -248,13 +248,13 @@ $\mathrm{L}$, $\mathrm{M}$ is true, that is $\mathrm{WA}$
is equivalent to the disjunction $\mathrm{C}\vee\mathrm{L}\vee\mathrm{M}$.
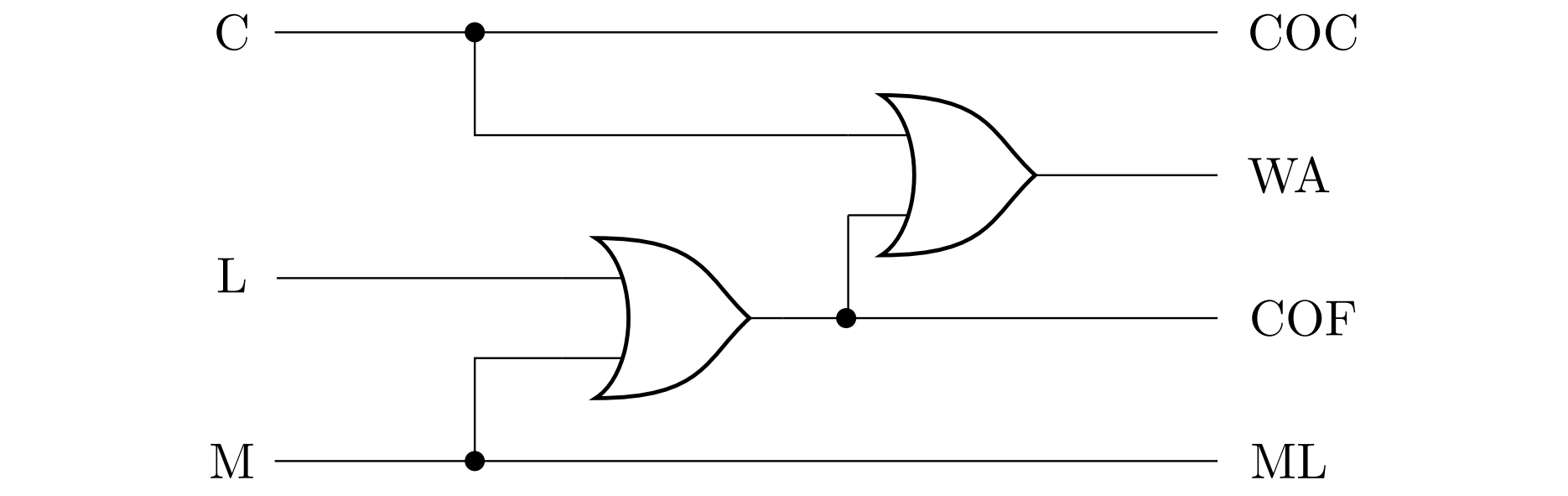
The following figure shows a diagram of the corresponding circuit - the disjunction
-$\mathrm{C}\vee\mathrm{L}\vee\mathrm{M}$ is realized by inserting two OR terms,
+$\mathrm{C}\vee\mathrm{L}\vee\mathrm{M}$ is implemented by inserting two OR terms,
i.e. as $\mathrm{C}\vee\left( \mathrm{L}\vee\mathrm{M}\right)$.
All the mentioned exercises can be illustrated on various logic circuit simulators,
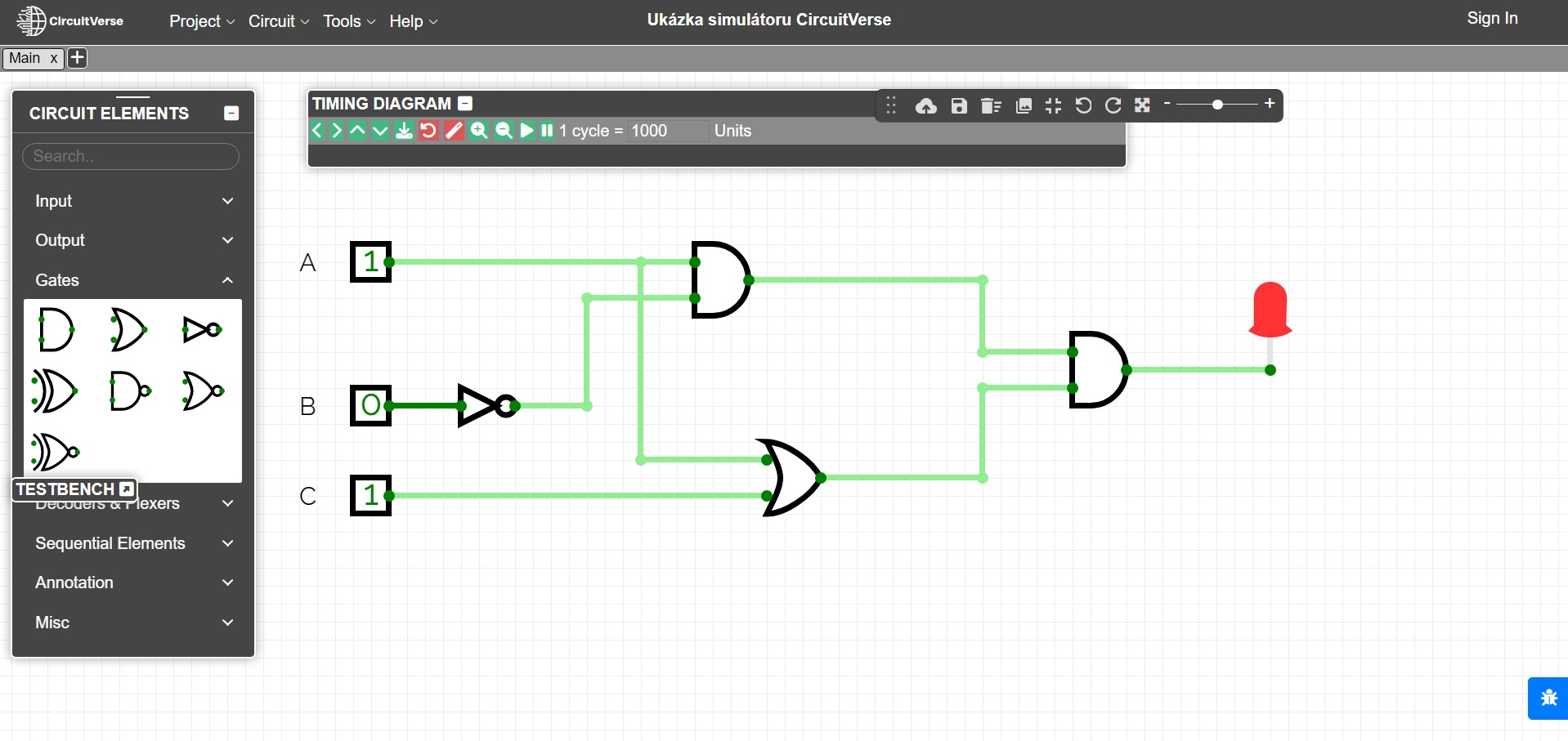
-e.g. CircuitVerse online simulator. In the last figure, the circuit from Exercise 2 is modeled in this simulator.
+e.g. CircuitVerse online simulator. In the last figure, the circuit from Exercise 2 is modeled using this simulator.
It is also possible to use specialized electronic kits for illustration.