diff --git a/00025_Dried_Tomatoes/en_article_proofreading.md b/00025_Dried_Tomatoes/en_article_proofreading.md
index fb0d9c0..475de63 100644
--- a/00025_Dried_Tomatoes/en_article_proofreading.md
+++ b/00025_Dried_Tomatoes/en_article_proofreading.md
@@ -2,8 +2,8 @@
keywords:
- percentages
- inverse proportion
-- linear fractional function
-is_finished: False
+- rational function
+is_finished: True
---
@@ -19,7 +19,7 @@ In households, fruits, vegetables or mushrooms are dried freely in the sun, in a
Commercial drying of fruit then takes place in specialized dehydrators.
When drying, it is important that each piece is exposed to a constant flow of warm air,
-which evaporates the water and lowers the humidity. The humidity should drop to a maximum of $30\,\%$.
+which evaporates the water and lowers the humidity. The humidity should drop to a maximum of $30\%$.
At this humidity, the growth of microorganisms and mold is prevented,
regardless of the packaging material and the storage temperature.
@@ -27,31 +27,31 @@ regardless of the packaging material and the storage temperature.
Tomatoes are one of the typical vegetables that are dried.
Some lovers of Italian cuisine consider them a little red miracle. In terms of drying,
-tomatoes are among the most demanding because they consist of $94\,\%$ water.
+tomatoes are among the most demanding because they consist of $94\%$ water.
-All percentages in the following exercises are by mass,
+All percentages in the following exercises are expressing mass fractions,
i.e. they numerically represent the number of grams of the component in $100\,\text{g}$ of mass.
> **Exercise 1.** If a kilogram of fresh tomatoes loses one percentage point of water after drying,
-> how many grams will the tomatoes weigh? Just for fun, try to guess the answer first.
+> how many grams will the tomatoes weigh? Just for fun, try guessing the answer first.
*Solution.* One kilogram of fresh tomatoes is made up of $940\,\text{g}$ of water
and $60\,\text{g}$ of residual substances (called dry matter).
-After drying to a water content of $93\,\%$, let us denote the unknown mass of the tomato as $x$ (in grams).
+After drying to a water content of $93\%$, let us denote the unknown mass of the tomato as $x$ (in grams).
Since the dry matter remains in the tomato, the water in the tomato now weighs $x-60\,\text{g}$, i.e.
$$
\frac{x-60}{x} = \frac{93}{100},
$$
since the ratio of the weight of the water to the total weight must be exactly $93/100$.
The solution to this equation is the mass of the tomatoes
-$$x=\frac{6000}{7}\doteq 857{,}14\,\text{g}.$$
+$$x=\frac{6000}{7}\doteq 857{.}14\,\text{g}.$$
-> **Exercise 2.** Determine the equation and the domain of a function
-> that describes the dependence of the actual weight of the tomatoes on the percentage of water
+> **Exercise 2.** Determine the formula and the domain of a function
+> that describes the relationship between the actual weight of the tomatoes and the percentage of water
> contained in them during the drying of one kilogram of fresh tomatoes.
> Sketch the graph of this function.
-*Solution.* From the assignment we know that the independent variable (denoted as usual by $x$)
+*Solution.* We know from the assignment that the independent variable (denoted as usual by $x$)
is the percentage of water in the tomatoes, and the dependent variable (denoted by $y$)
is the actual weight of the tomatoes (in grams). Thus
$$
@@ -64,19 +64,19 @@ $$
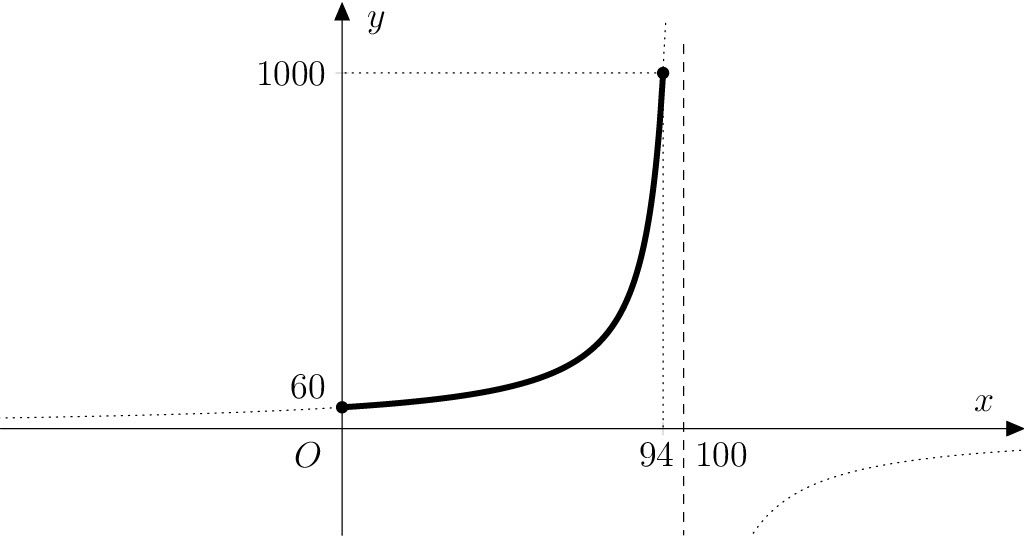
The domain of this function is the closed interval $\left\langle 0; 94 \right\rangle$,
where boundary values correspond to tomatoes completely dehydrated
-and fresh tomatoes with a water content of $94\,\%$.
+and fresh tomatoes with a water content of $94\%$.
The graph of the function $f$ lies on a hyperbola,
which is a shifted graph of the function $f_0\colon y = -\frac{6000}{x}$ by 100 units
in the direction of the positive semi-axis $x$.
-> **Exercise 3.** How does the analytic formula of the function from the previous exercise change
-> if we dry $m$ grams of fresh tomatoes in general?
+> **Exercise 3.** In general, how does the formula of the function from the previous exercise change
+> if we dry $m$ grams of fresh tomatoes?
-*Solution.* We start from the relation $(1)$ in the solution of Exercise 2,
+*Solution.* Let us begin with equation $(1)$ in the solution of Exercise 2,
where we replace the number $60$ (i.e. the weight of the dry matter in grams) by the general expression
-$\frac{6}{100}m$, because the dry matter makes up $6\,\%$ of the weight of fresh tomatoes.
+$\frac{6}{100}m$, because the dry matter makes up $6\%$ of the weight of fresh tomatoes.
By expressing the variable $y$, we get the formula of the function $g$ (with parameter $m$) as
$$
@@ -85,19 +85,19 @@ $$
> **Exercise 4.** How many kilograms of fresh tomatoes are needed to make
>
->1. one kilogram of dried tomatoes with a water content of $10\%$;
->2. $500\,\text{g}$ of dried tomatoes with $20\%$ water content;
->3. $250\,\text{g}$ of dried tomatoes with $40\%$ water content?
+> a. one kilogram of dried tomatoes with a water content of $10\%$;
+> b. $500\,\text{g}$ of dried tomatoes with $20\%$ water content;
+> c. $250\,\text{g}$ of dried tomatoes with $40\%$ water content?
*Solution.* If we refer to the function $g$ from the solution of Exercise 3,
we ask for which $m$ the graph of the function $g$ passes through a point with coordinates $[10;1000]$ (in case a),
or through a point with coordinates $[20;500]$ (in case b), or through point $[40;250]$ (in case c).
By successively substituting the coordinates of those three points for $x$
-and $y$ into the equation $(2)$ and solving the resulting linear equations,
+and $y$ into equation $(2)$ and solving the resulting linear equations,
we obtain the roots $m_1=15\,000$, $m_2=\frac{20\,000}{3}$ and $m_3=2500$.
-The results are therefore $15\,\text{kg}$ (for case a), $\frac{20}{3}\doteq 6{,}67\,\text{kg}$ (for case b)
-and $2{,}5\,\text{kg}$ (for case c).
+The results are therefore $15\,\text{kg}$ (for case a), $\frac{20}{3}\doteq 6{.}67\,\text{kg}$ (for case b)
+and $2{.}5\,\text{kg}$ (for case c).
## Literature