diff --git a/00021_First_Kepler_Law/en_article_proofreading.md b/00021_First_Kepler_Law/en_article_proofreading.md
index fca198a..7167aab 100644
--- a/00021_First_Kepler_Law/en_article_proofreading.md
+++ b/00021_First_Kepler_Law/en_article_proofreading.md
@@ -4,52 +4,56 @@ keywords:
- ellipse
is_finished: False
---
-
-# Kepler's First Law of planetary motion
+<!-- Navrhuji spíše drobnější změny - většinou zpřesňující význam tvrzení.
+- "Earth" se většinou píše bez členu "the"
+- Správná terminologie pro elipsu je "semi-major a semi-minor axes" místo "major and minor semi-axes" viz např. zde
+https://en.wikipedia.org/wiki/Semi-major_and_semi-minor_axes -->
+# Kepler's First Law of Planetary Motion
Kepler's first law states:
-*The planets move around the Sun in elliptical trajectories, with the Sun at one of their foci.*
+*The planets move around the Sun in elliptical trajectories, with the Sun located at one of their foci.*
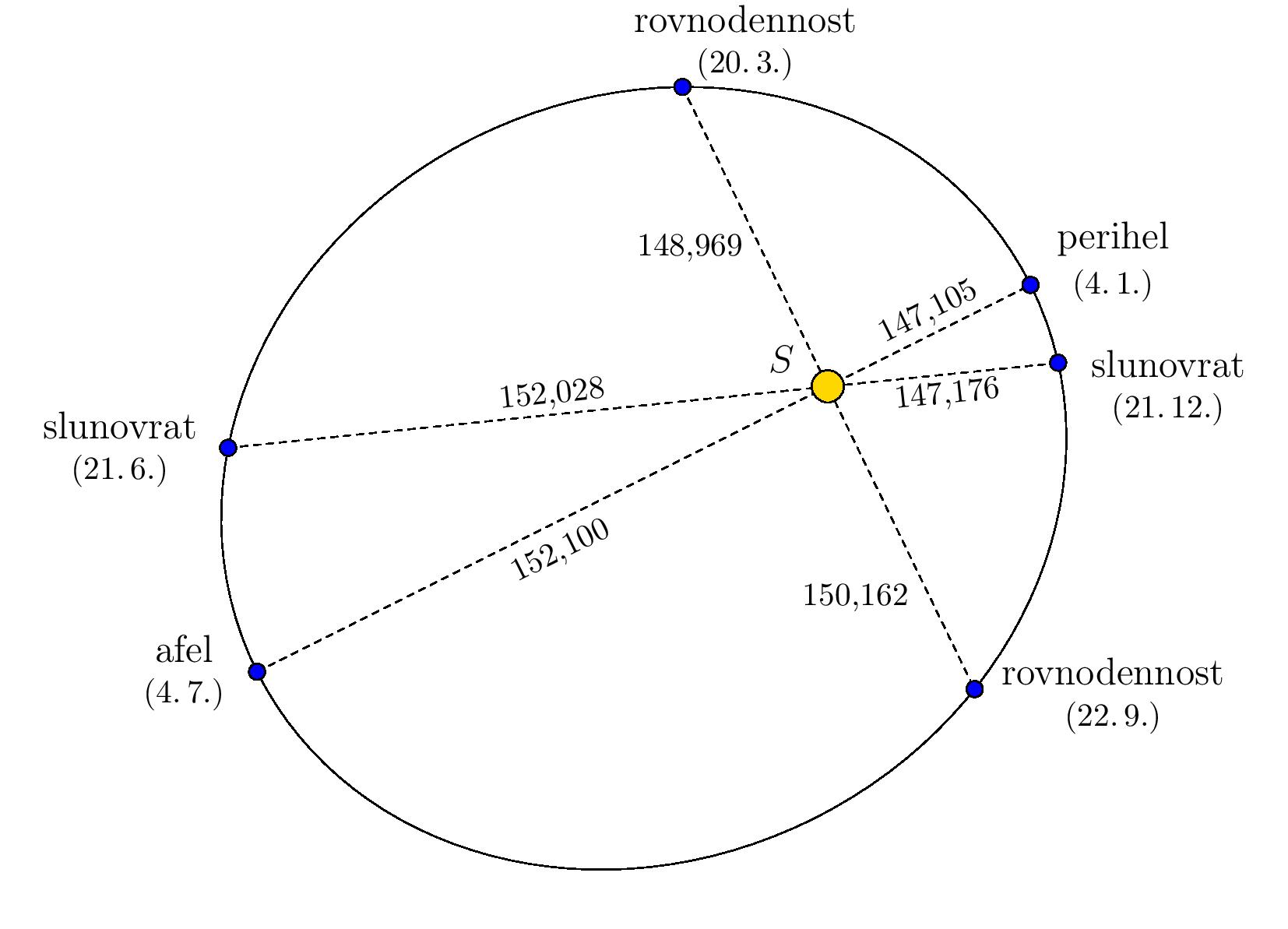
-The place on the trajectory where the Earth is closest (or farthest) to the Sun
-is then called *perihelion* (or *aphelion*).
-The situation is shown in the following figure, which is deliberately distorted
+The point on the trajectory where Earth is closest (or farthest) to the Sun
+is called *perihelion* (or *aphelion*).
+The situation is shown in the following figure, which is intentionally distorted
so that the elliptical shape of the trajectory is visible.
-The distances are given in millions of kilometers
-(data are from the Stellarium program and correspond to the year 2022).
+Distances are given in millions of kilometers, based on
+data from the Stellarium program, and correspond to the year 2022.
-
+
-> **Exercise 1.** Determine the eccentricity and lengths of the major and minor
-> semi-axes of Earth's elliptical trajectory using the information in the figure.
+> **Exercise 1.** Using the information in the figure, determine the eccentricity and the lengths of the semi-major and semi-minor
+> axes of Earth's elliptical trajectory.
*Solution.* Since the Sun is at one of the foci of the ellipse,
aphelion and perihelion are its main vertices.
-The sum of the distances of the Sun from the Earth at aphelion and perihelion is therefore twice the length of the major semi-axis $a$ and thus
+Therefore, the sum of the distances from the Sun to Earth at aphelion and perihelion is twice the length of the semi-major axis $a$. Thus,
$$a=\frac{152{,}100\cdot10^6\,\text{km} + 147{,}105\cdot10^6\,\text{km}}{2}\doteq149,603\cdot10^6\,\text{km}.$$

-As can be seen from the figure (the point $O$ here marks the centre of the ellipse),
-the sum of the length of the major semi-axis $a$ and the eccentricity $e$ is the distance of the Sun from the Earth in the aphelion. Thus
+As seen in the figure (where point $O$ represents the center of the ellipse),
+the difference between the distance from the Sun to Earth at aphelion and the length of the semi-major axis $a$ gives the eccentricity $e$. Thus
$$e=152,100\cdot10^6\,\text{km} - 149,603\cdot10^6\,\text{km} =2,497\cdot10^6\,\text{km}.$$
-Because the relation $a^2 = b^2 + e^2$ holds in the ellipse
-(where $b$ is length of the minor semi-axis),
-we will now determine the length of the minor semi-axis:
+Since for an ellipse the relation $a^2 = b^2 + e^2$ holds,
+where $b$ is the length of the semi-minor axis,
+we can now determine the length of the semi-minor axis:
$$b=\sqrt{a^2 - e^2}\doteq 149,582\cdot10^6\,\text{km}.$$
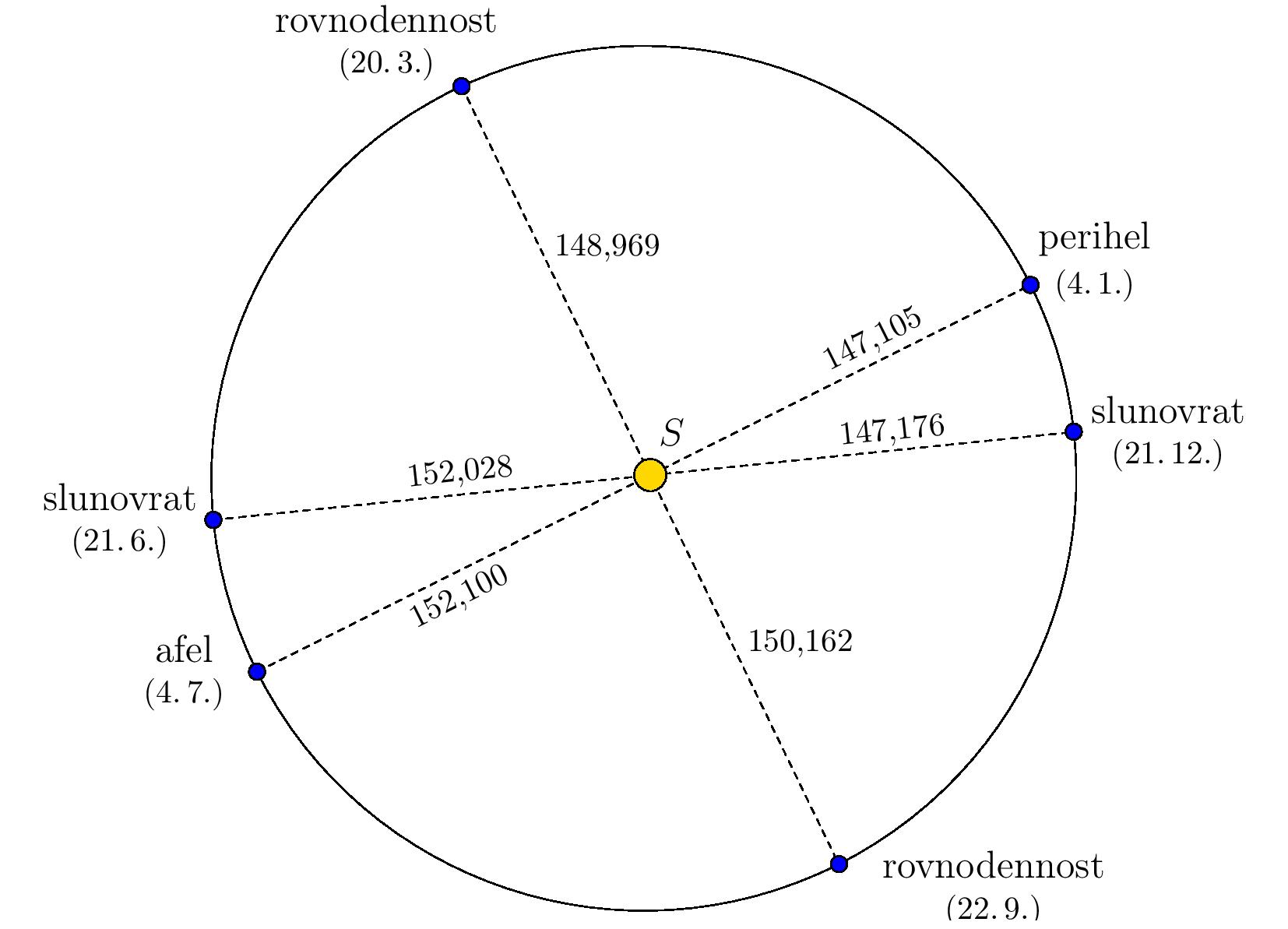
-If we now redraw the image from the assignment so that the ratio
-of the sizes of the semi-axes corresponds to reality,
-it can be seen that the trajectory is indeed very similar
-to a circle with the Sun at its center.
+If we now redraw the figure from the exercise so that the ratio
+of the lengths of the axes corresponds to reality,
+it is evident that the shape of the trajectory is indeed very close
+to a circle, with the Sun at its center.
-
+
## Literature
* Stellarium contributors (2023). *Stellarium 23.4.*[software], <https://stellarium.org/cs/>
+