diff --git a/00018_Hyperbolic_navigation/en_article_proofreading.md b/00018_Hyperbolic_navigation/en_article_proofreading.md
index 3349abd..90ce369 100644
--- a/00018_Hyperbolic_navigation/en_article_proofreading.md
+++ b/00018_Hyperbolic_navigation/en_article_proofreading.md
@@ -18,55 +18,48 @@ so the signal delay determines the difference between the distances of the vesse
The set of points that have a constant difference in distances
from two given fixed points is a hyperbola.
-Thus we know that the vessel is located on a hyperbola
+Thus, the vessel is located on a hyperbola,
whose foci are the transmitters, and which is determined
-by the difference in the distance of the vessel from these transmitters.
-The delay of the signal from another pair of stations then determines the second hyperbola on which the vessel must lie. If the vessel lies on both hyperbolas,
+by the difference in the vessel’s distances from those transmitters.
+The signal delay from another pair of stations then determines the second hyperbola on which the vessel must lie. If the vessel lies on both hyperbolas,
it lies at their intersection.
-The set of points, that have a constant difference
-in distance from two given fixed points is a hyperbola.
-Thus, the vessel is located on the hyperbola,
-whose foci are just the transmitters,
-and which is determined by the difference in the vessel's distance from those transmitters.
-The signal delay from another pair of stations then determines the second hyperbola on which the vessel must lie.
-If the vessel lies on both hyperbola,
-it lies at the intersection of them.
+<!-- Tento odstavec mažu - byl tady 2x -->
> **Exercise 1.** Three receivers $P_1$, $P_2$, and $P_3$ are deployed in the landscape.
> The figure captures the distances we know:
> 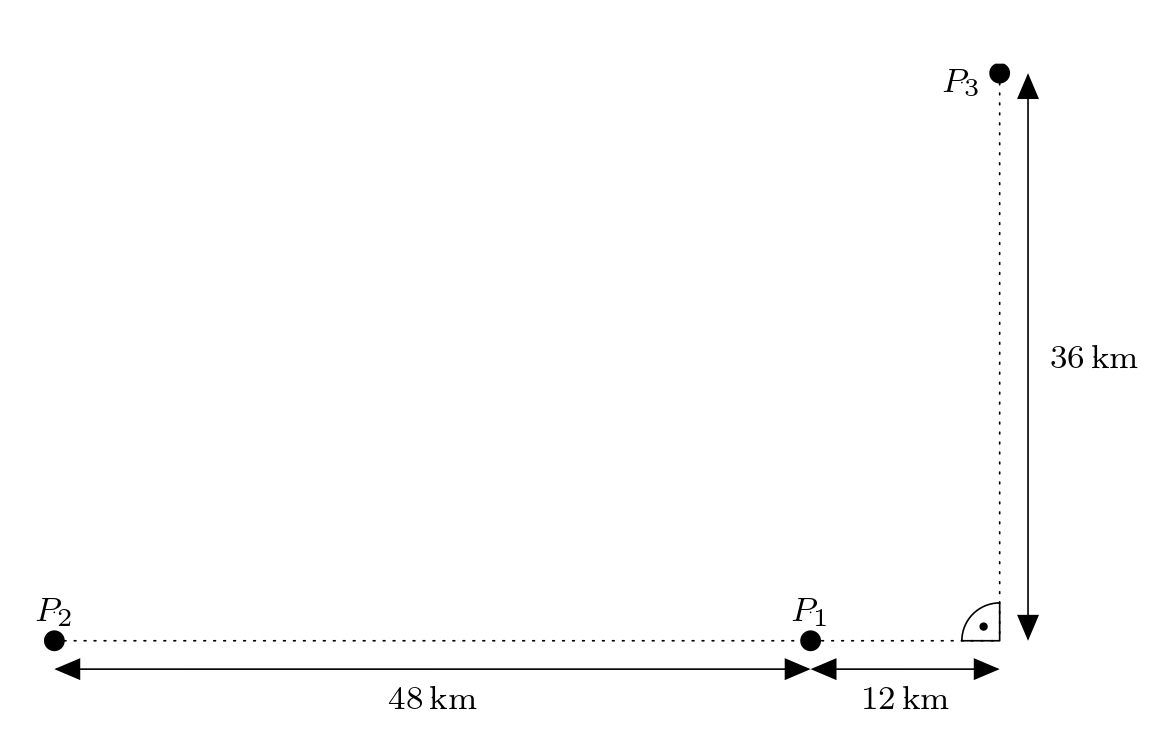
> Adam's tourist navigation will send a signal to all three receivers.
-> Signal arrives at receiver $P_1$ and $P_3$ at the same time
-> and at reciever $P_2$ 80 microseconds later.
+> Signal arrives at receivers $P_1$ and $P_3$ at the same time
+> and at receiver $P_2$ 80 microseconds later.
> Where is Adam located?
> Assume the signal travels 300 000 km per second.
> Determine the position in a suitably established coordinate system.
-*Solution.* First, choose the suitable Cartesian coordinate system in the figure.
-We justify the choice as follows: because Adam is equally distant from the receiver $P_1$ and $P_3$,
-his position is on the axis of line $P_1P_3$.
-The fact that his signal arrives at receiver $P_2$ 80 microseconds later than at receiver $P_1$ means that,
-it is $24\,\text{km}$ further from receiver $P_2$ than it is from receiver $P_1$.
+*Solution.* First, in the figure, we choose a suitable Cartesian coordinate system.
+We justify this choice as follows: Since Adam is equidistant from receivers $P_1$ and $P_3$,
+he is positioned on the axis of line $P_1P_3$.
+The fact that his signal arrives at receiver $P_2$ 80 microseconds later than at receiver $P_1$ means that
+Adam is $24\,\text{km}$ further from receiver $P_2$ than from receiver $P_1$.
His position is therefore also on the branch of the hyperbola $h$ with foci $P_1$ and $P_2$
-(where the difference of Adam's distances from $P_1$ and $P_2$ is just $24\,\text{km}$).
-It is advantageous to place the origin of the coordinate system in the center of the segment $P_1P_2$
-so that the hyperbola $h$ has the simplest possible equation.
+(where the difference in Adam's distances from $P_1$ and $P_2$ is just $24\,\text{km}$).
+It is advantageous to place the origin of the coordinate system in the center of the line segment $P_1P_2$
+so that the equation of hyperbola $h$ has the simplest possible form.
Let us denote the origin of the system $O$
-and place it in the centre of the line segment $P_1P_2$.
+and place it in the center of the line segment $P_1P_2$.
The positive direction of the $x$-axis will be determined by the semi-line $OP_1$
-and we choose the positive direction of the $y$-axis so that the second coordinate of the point $P_3$ is positive.
+and we choose the positive direction of the $y$-axis so that the second coordinate of point $P_3$ is positive.
Since all the given dimensions are multiples of $12$,
we choose the units on both axes
-to correspond a distance of $12\,\text{km}$.
+to correspond to a distance of $12\,\text{km}$.
The situation is illustrated in the figure:
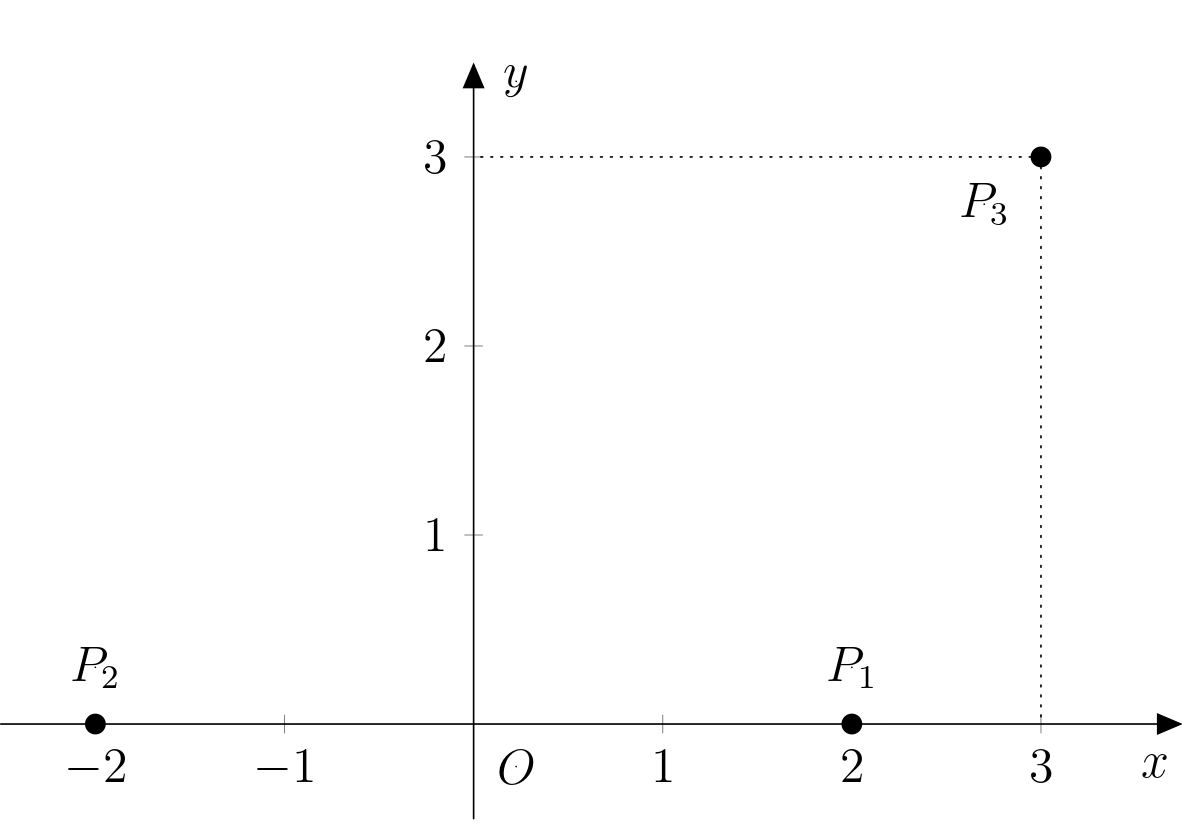
-Let us denote the unknown position of Adam by $A$.
-We know that the point $A$ lies on the axiof the segments
-$P_1P_3$, therefore, we express this axis (let's denote it $o$) parametrically:
+Let $A$ denote the unknown position of Adam.
+We know that the point $A$ lies on the axis of the line segment
+$P_1P_3$. We express this axis (let's denote it $o$) parametrically:
$$o\colon X = S_{P_1P_3}+t\cdot \overrightarrow{u_o},$$
where $S_{P_1P_3}\left[\frac{5}{2};\frac{3}{2}\right]$
and $\overrightarrow{u_o}=(3;-1)$. Then
@@ -78,24 +71,25 @@ y &= \tfrac{3}{2} - t,\quad t\in\mathbb{R}.
\end{aligned}
$$
-Let us now determine the equation of the hyperbola.
-Since the points $P_1$ and $P_2$ are the foci of the hyperbola $h$,
-the center of the hyperbola is the point $O$
-and its eccentricity $e$ is equal to half of $|OP_1|$, thus $e=2$. Next,
+To find the equation of the hyperbola, note that
+the points $P_1$ and $P_2$ are the foci of the hyperbola $h$,
+with center $O$
+and eccentricity $e$ equal to half of $|OP_1|$, thus $e=2$. Next,
since the difference $|AP_1|-|AP_2|=2$
is twice the length of the major semiaxis of the hyperbola,
-the length of major semiaxis $a$ is equal to $1$.
+the length of the major semiaxis $a$ is equal to $1$.
We calculate the length of the minor semiaxis $b$ by substituting into the relation
$b=\sqrt{e^2-a^2}=\sqrt{4-1}=\sqrt{3}$.
-Now we can write down the equation of the required hyperbola
+Now, we can write down the equation of the required hyperbola
$$h\colon x^2-\frac{y^2}{3}=1.$$
The point $A$ lies on its right branch (it is closer to the receiver $P_1$),
i.e., its first coordinate must necessarily be $x_A>0$.
Let us now calculate the coordinates of the intersections
of the line $o$ and the hyperbola $h$.
-By substituting the parametric equations of the line segment
-into the equation of the hyperbola, we get
+By substituting the parametric equations of the line $o$
+<!-- tady jsem nahradila "line segment" výrazem "line $o$", protože parametrické rovnice, odvozené výše, určují celou přímku o, ne jen úsečku. Nevím jestli to není špatně i v češtině. -->
+into the equation of the hyperbola, we get:
$$
\begin{aligned}
\left(\frac{5}{2} + 3t\right)^2-\frac{\left(\frac{3}{2}-t\right)^2}{3} &= 1 \\
@@ -104,22 +98,21 @@ $$
52 t^2 +96t +27 &= 0
\end{aligned}
$$
-The roots of this quadratic equation are $t_1=-\frac{9}{26}$ and $t_2=-\frac{3}{2}$. We substitute $t_1$ into the parametric equations and get
-
+The roots of this quadratic equation are $t_1=-\frac{9}{26}$ and $t_2=-\frac{3}{2}$. We substitute $t_1$ into the parametric equations and get:
$$
\begin{aligned}
x_1 &= \tfrac{5}{2} + 3\cdot \left(-\tfrac{9}{26}\right) = \tfrac{19}{13}\\
y_1 &= \tfrac{3}{2} - \left(-\tfrac{9}{26}\right) = \tfrac{24}{13},
\end{aligned}
$$
-that is $A_1\left[ \tfrac{19}{13};\tfrac{24}{13} \right]$. Similarly, by substituting $t_2$, we get
+that is $A_1\left[ \tfrac{19}{13};\tfrac{24}{13} \right]$. Similarly, by substituting $t_2$, we get:
$$
\begin{aligned}
x_2 &= \tfrac{5}{2} + 3\cdot \left(-\tfrac{3}{2}\right) = -2\\
y_2 &= \tfrac{3}{2} - \left(-\tfrac{3}{2}\right) = 3,
\end{aligned}
$$
-i.e. $A_2 \left[ -2;3 \right]$.
+i.e., $A_2 \left[ -2;3 \right]$.
However, the point $A_2$ does not satisfy the condition $x_A > 0$ (it lies on the second branch of the hyperbola),
thus we get the only possible position of Adam,
namely $A\left[ \tfrac{19}{13};\tfrac{24}{13} \right]$.