diff --git a/00017_Shadow_of_the_house/en_article_proofreading.md b/00017_Shadow_of_the_house/en_article_proofreading.md
index bd24ff5..9999808 100644
--- a/00017_Shadow_of_the_house/en_article_proofreading.md
+++ b/00017_Shadow_of_the_house/en_article_proofreading.md
@@ -5,66 +5,67 @@ keywords:
is_finished: False
---
-# Shadow of the house
+# Shadow of House
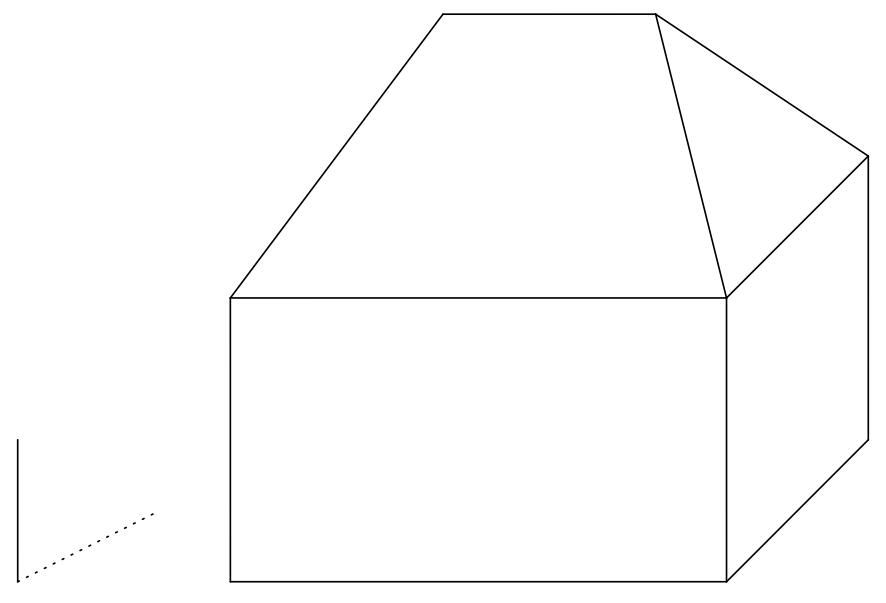
-Martin wants to set up space on his canvas to draw a house on a sunny day.
-Therefore, he visualized in a cabinet axonometry a simple model of a house
-that stands on a horizontal flat ground.
-House is formed by a rectangular cuboid with simple hip roof.
-*Hip roof* is the roof of a house formed by two isosceles triangles and two
-isosceles trapezoids. All four roof planes have the same slope. He also placed
-on canvas a vertical pole and its shadow next to the house (see the figure).
+Martin wants to set up a space on his canvas to draw a house on a sunny day.
+Therefore, he visualized a simple model of a house
+in a parallel (orthographic) projection, standing on a horizontal flat ground.
+House is formed by a rectangular cuboid with a simple hip roof.
+*Hip roof* is a roof formed by two isosceles triangles and two
+isosceles trapezoids. All four roof planes have the same slope. On a canvas next to the house, he placed a vertical rod and its shadow(see the figure).
+<!--“cabinet axonometry” nejspíš není špatně, ale po zkoumání tohoto termínu si myslím, že patří do odborné technické praxe a na střední škole se to nepoužívá. Nejsem odborník na stereometrii, ale nějak si myslím, že na to co je v úloze použito stačí “parallel projection” nebo “orthographic projection” což by měly být termíny se kterými se stuenti ve stereometrii setkají.
-We will need the following terms to describe the solution:
+“pole” měním na “rod” protože v dalším textu používáte termín “rod”, tak ať je název stejný, když jde pořád o stejnou tyč. -->
-* *Self shadow* is the unlit part of the object's surface.
-A closed line on the surface of an object that separates the illuminated
-and the unlit part, is called *self shadow boundary*.
+
+To describe the solution, we will need the following terms:
+
+* *The self shadow* of an object is the unlit part of the object's surface.
+A closed line on the surface of the object that separates the lit
+and the unlit parts is called *the boundary of the self shadow*.
* *The cast shadow* of an object is the projection of the object
in the direction of the light rays onto the given plane.
It holds that *the boundary of the cast shadow is the cast shadow
of the boundary of the self shadow*
-> **Exercise 1.** Draw the self shadow of the house in the picture and
-> the shadow cast on the ground by the sun.
->
+>**Exercise 1.** Mark on the figure the self shadow of the house and
+>the shadow of the house cast on the ground by the sun. (The distance from the Sun to the surface of the Earth is so great that we can consider the sun rays to be parallel to each other.)
>
+<!-- V první větě zadání doporučuji zůstat u termínu “figure”, když byl použit v prvním odstavci při odkazu na obrázek. Tj . myslím je celkem jedno jestli budeme používat “picture” nebo “figure”, ale v rámci textu doporučuji konzistenci.
+V české verzi je věta o tom, že paprsky slunce lze považovat za rovnoběžné, tak jsem ji přidala i do EN verze.-->
+
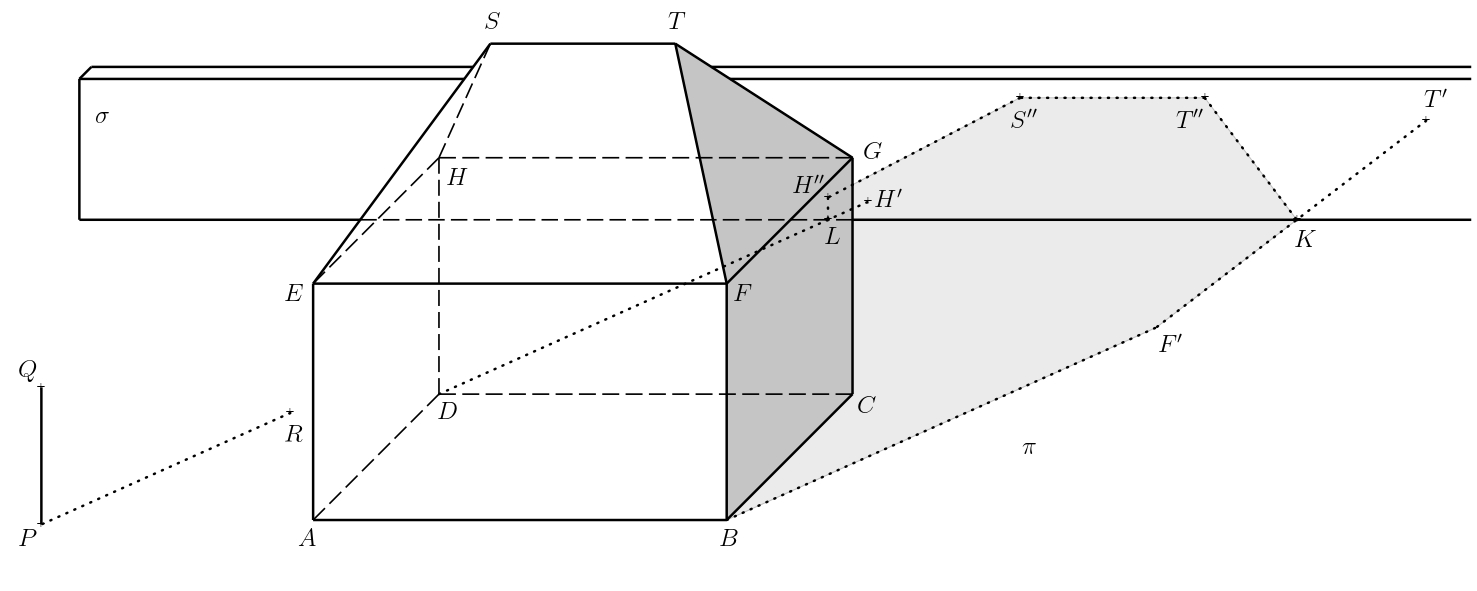
*Solution.* Let $P$ denote the base of the rod, $Q$ its upper end, and $R$ the cast shadow of point $Q$.
The oriented segment $QR$ thus determines the direction and orientation of the light rays.
-the line $PR$ is the orthogonal projection of the line $QR$ into plane of the ground.
-The plane of the ground will be denoted $\pi$ in the following text
-(we approximate the ground by a plane denoted $\pi$ in the following text).
-Next, let us mark the vertices of the rectangular cuboid $ABCDEFGH$
-and denote the endpoints of the roof ridge by $S$ and $T$.
-
-The illuminated part of the house is the left side and front side
-of the rectangular cuboid and corresponding parts of the roof.
+The line $PR$ is the orthogonal projection of the line $QR$ into plane of the ground.
+In the following text, we denote the plane of the ground by $\pi$. Next, let us denote the vertices of the rectangular cuboid $ABCDEFGH$ and denote the endpoints of the roof’s ridge by $S$ and $T$.
+
+The illuminated part of the house includes the left side and the front side
+of the rectangular cuboid and the corresponding parts of the roof.
The boundary of the self shadow is thus the closed polygonal chain $ABFTSHDA$.
To determine the boundary of the cast shadow of the house, it is sufficient
to construct the cast shadows of the vertices of this polygonal chain.
Of these, $A$, $B$ and $D$ already lie in the plane $\pi$
-and and that's why they are also their own cast shadows. Therefore,
-it is sufficient to construct the cast shadows of points $F$, $T$, $S$ and $H$.
+and that's why they also are their own cast shadows. Therefore,
+it is sufficient to construct the cast shadows of points $F$, $T$, $S$, and $H$.
The shadow cast by point $T$ is the intersection of the light ray
-passing through it, with the perpendicular projection of this ray into
-the $\pi$ plane. Recall that the direction of the light rays is
-determined by the straight line $QR$ and the direction of the
+passing through it with the perpendicular projection of this ray into
+the plane $\pi$. Recall that the direction of the light rays is
+determined by the line $QR$, and the direction of the
perpendicular projection of the rays into the plane $\pi$ is
determined by the line $PR$.
-The perpendicular projection of the beam further passes through point $T_1$,
+The perpendicular projection of the ray further passes through point $T_1$,
which is the perpendicular projection of the point $T$ onto the plane $\pi$.
If we denote the cast shadow of point $T$ as $T'$,
its construction is shown in the figure.
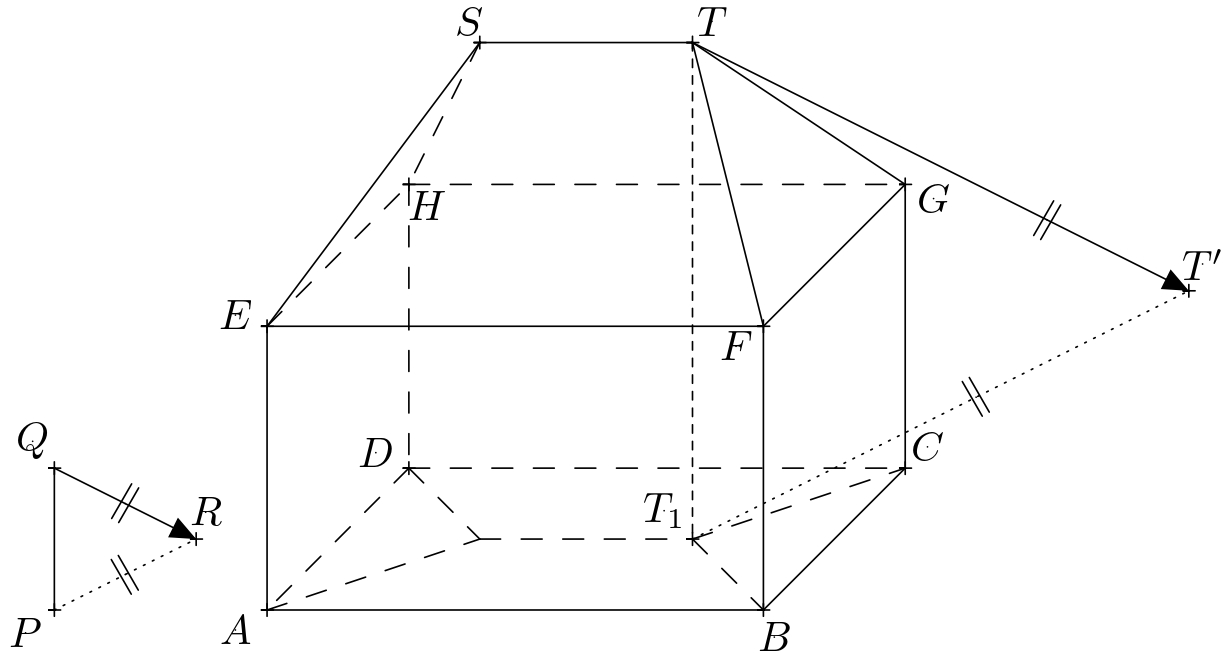
-We construct the cast shadows $F'$, $S'$, $H'$ of the points $F$, $S$
+We construct the cast shadows $F'$, $S'$, $H'$ of the points $F$, $S$,
and $H$ similarly.
The boundary of the cast shadow of the house is then the polygon $ABF'T'S'H'D$.
-When shading, we take into account only the visible parts of self
-shadow and the cast shadow.
+When shading, we consider only the visible parts of the self and cast shadows.
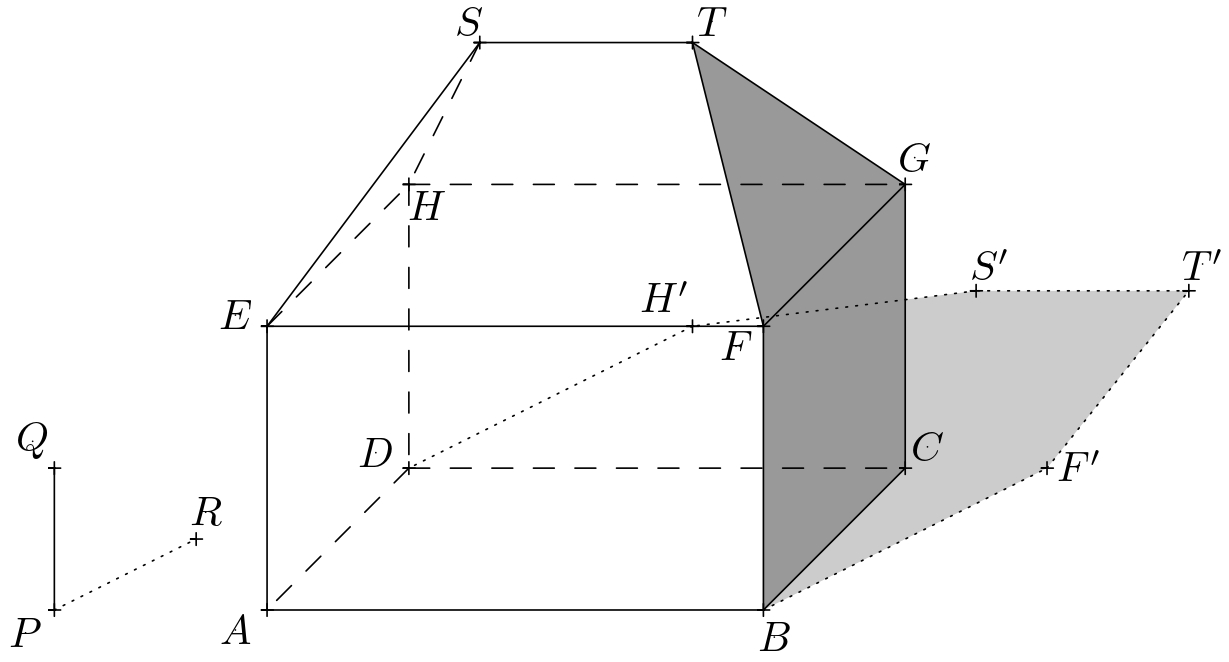
@@ -73,16 +74,15 @@ shadow and the cast shadow.
> back walls of the house. 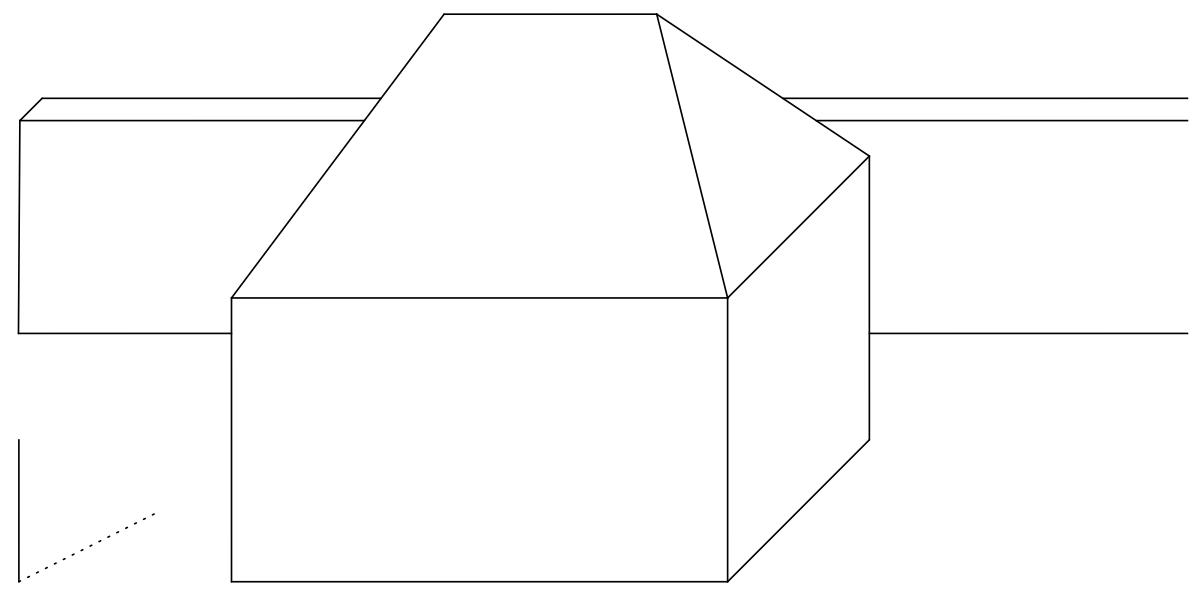
-*Solution.* The house's self shadow, its boundary and cast shadows of
-points in the $\pi$ plane, which are located in front of the wall from
-our point of view will remain unchanged. Let us denote by $\sigma$
-the plane in which the front side of the added wall of the house lies.
-For the triplet of points $T$, $S$ and $H$, it is necessary to
+*Solution.* The house's self shadow, its boundary, and the cast shadows of
+points into the plane $\pi$, which are from our prospective located in front of the wall, remain unchanged. Let us denote by $\sigma$
+the plane in which the front side of the added wall lies.
+For the trio of points $T$, $S$, and $H$, it is necessary to
construct their cast shadows onto this plane. We will describe the
-construction again only for the $T$ point.
+construction only for point $T$ again.
Consider the points $T_1$ and $T'$ from the previous exercise.
-Let $\tau$ denote the plane $TT_1T'$ and further let us denote
+Let $\tau$ denote the plane $TT_1T'$, and further let us denote
by $U$ the intersection of the line $T_1T'$
and the bottom edge of the wall (i.e., $\sigma\cap\pi$).
@@ -90,26 +90,25 @@ and the bottom edge of the wall (i.e., $\sigma\cap\pi$).
wall](math4you_00017_reseni_b1.jpg)
The intersection of the planes $\sigma$ and $\tau$ must also pass
-through this point, i.e., the shadow $T_1T$ cast on the $\sigma$
-plane.
+through this point, i.e., the shadow $T_1T$ cast onto the
+plane $\sigma$.
Moreover, this intersection must be vertical because both $\tau$ and
$\sigma$ are vertical.
-The cast shadow of the point $T$ in the $\sigma$ plane (let's denote it by $T''$)
-then it lies on the said intersection and the line $TT'$.
+The cast shadow of the point $T$ into the plane $\sigma$ (let's denote it by $T''$)
+then lies on the said intersection and the line $TT'$.
We construct the cast shadows $S''$, $H''$ of points $S$ and $H$
similarly. The boundary of the self shadow is then the closed
polygonal chain $ABF'KT''S''H''LDA$, where $K$ (resp. $L$) lies on the
-intersection of the planes $\sigma$ and $\pi$ and further lies on the
-segment $F'T'$ (resp. $DH'$). We are shading only the visible parts
-of self shadow and cast shadow, we are not shading the parts of the
-shadow behind the house.
+intersection of the planes $\sigma$ and $\pi$, and also lies on the
+segment $F'T'$ (resp. $DH'$). We shade only the visible parts
+of the self and cast shadows, we do not shade the parts of the
+shadow obscured by the house.
-*Note.* For a better idea, the interactive applet in GeoGebra can also help.
-The direction of the sun's rays can be modified to a certain extent
-there, see <https://www.geogebra.org/m/ecyqv4qg>
+*Note.* For better visualization, an interactive applet in GeoGebra may also help.
+In the applet, the direction of the sun's rays can be modified to a certain extent, see https://www.geogebra.org/m/ecyqv4qg
## Literature