diff --git a/00015_Finite_Linear_Games/en_article_proofreading.md b/00015_Finite_Linear_Games/en_article_proofreading.md
index af7264c..13532b4 100644
--- a/00015_Finite_Linear_Games/en_article_proofreading.md
+++ b/00015_Finite_Linear_Games/en_article_proofreading.md
@@ -8,37 +8,37 @@ is_finished: False
# Finite linear games
-Many computer and mobile games are based on puzzles in which to
-achieve the goal you need to perform a certain combination of
-moves. For example, to press some of the offered switches so the
-machine controlled by them, would work. Moreover, such switches have
-a finite number of the states in which they may be: they are either on
-or off. Let's demonstrate it on example of a light bulb. It is either
-on or off, and its switch only performs two actions. When the bulb is
-off, the first use of the switch turns it on and the second use of the
-switch turns it off. In informatics there is many such systems that
-have limited number of states. Those games, in which is necessary to
-set up the optimal combination of moves that will give us the correct
-outcome is called finite linear games.
+Many computer and mobile games are based on puzzles where achieving the goal requires performing a certain combination of
+moves. For example, flipping some of the offered switches to activate a
+device controlled by them. Moreover, such systems of switches usually have a finite number of states, with the switches mainly being either on
+or off. Let's take a light bulb as an example. It is either
+on or off, so its switch only performs two actions. When the bulb is
+off, the first use of the switch turns it on, and the second use turns it off. In computer science, there are many such systems that
+have a limited number of states. Specifically, the games in which it is necessary to
+set up the optimal combination of moves to bring the system to the desired state are called finite linear games.
+
+<!-- Tento odstaveček jsem potřebovala více přeformulovat. Část mi nedávala správný smysl – musím řici ani v češtině. Změn jsem udělala více, ale ne vše zvládnu zde zdůvodňovat. Pokud by jste s navrženými změnami nesouhlasili , něco nedávalo smysl, můžeme změny probrat osobně.
+Např. v angličtině raději třeba “flip the switch” ale ne “press the switch”
+když “press” tak “button” aj. …-->
+
## Game with three light bulbs
-Imagine a network of three light bulbs that are all off at the start
-and under each of them there's a switch. Each of the switches changes
-the state (on or off) of the bulbs above it and at the same time the
-bulbs directly adjacent to it. If we name the bulbs and their
-corresponding switches A, B, C, then pressing switch A will light bulb
-A, but because it is on the edge, only bulb B will light with it. The
-same applies to bulb C, it also has a neighbour on one side only, so
-pressing switch C will light up bulbs C and B. Only bulb B is adjacent
-to both A and C, so switch B changes the state of all three bulbs.
-
-In the following three images we can observe, how the light bulbs
-would gradually turn on and off when pressing buttons A and B in
-sequence. It is important to note that the order in which the buttons
-are pressed does not matter. We can imagine that if we first pressed
-B, all the bulbs will light up, and a subsequent press A turns off
-bulbs A and B so only the light of bulb C stays on.
+Imagine a circuit with three light bulbs that are initially all turned off, each with a switch button underneath. Each of these buttons changes
+the state (turns on or off) of the bulb above it and at the same time the
+two bulbs directly adjacent to it. If we name the bulbs and their
+corresponding buttons A, B, C, then pressing button A will light bulb
+A, but because it is on the edge, only bulb B will light up with it. The
+same applies to bulb C, it also only has one neighbour, so
+pressing button C will light up bulbs C and B. Only bulb B is adjacent
+to both A and C, so button B changes the state of all three bulbs.
+<!-- “network of light bulbs” je divné slovní spojení. Běžně se používá v češtině I v angličtině “obvod se žárovkami” tj. “circuit with light buulbs”.
+V tomto odstavečku je použito “switches A,B,C” zatímco v dalším odstavci “buttons A, B, C”, tak měním pro konzistenci na “buttons” -->
+
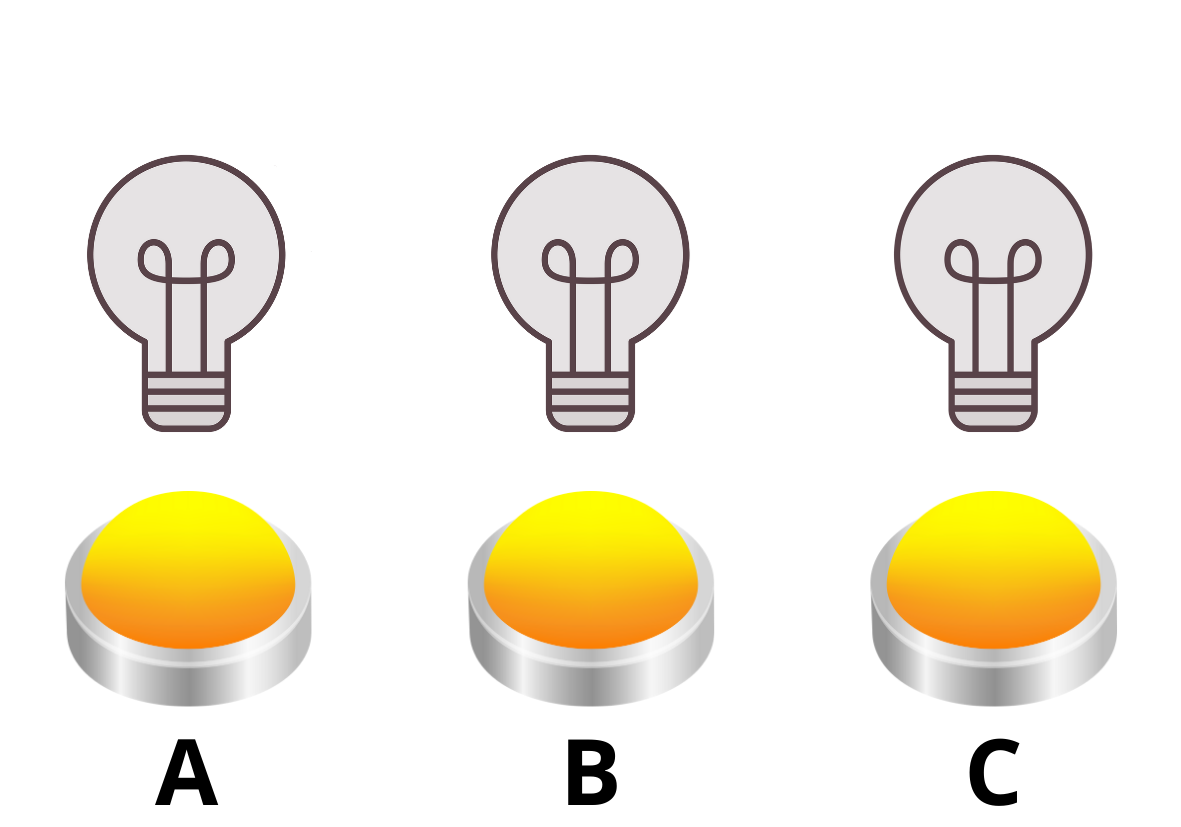
+In the following three images, we can observe how the light bulbs
+would gradually turn on and off when buttons A and B are pressed sequentially. It is important to realize that the order in which the buttons
+are pressed does not matter. We can imagine that if we first pressB, all the bulbs will light up, and then pressing A will turn off
+bulbs A and B, so only the bulb C stays lit up.
@@ -46,48 +46,41 @@ bulbs A and B so only the light of bulb C stays on.

-For the following exercises, the concept of a finite number is
-crucial. In the case of light bulbs that are always either on, or
-off, we can identify several situations, which are either happening
-("yes") or not happening ("no"), and since we are in math we can use
-instead of words binary system marking: yes = 1, no = 0, i.e.
+For the following exercises, the key concept is the existence of a finite number of possible states. In the case of light bulbs that are always either on or
+off, we can identify several situations, which either occur
+("yes") or do not occur ("no"), and since we are in math, instead of words, we can use binary notation: yes = 1, no = 0, i.e.,
- the bulb is on (1) or off (0),
-- the button controls the bulb (1) or has no effect (0),
-- the button is pressed (1) or not used (0).
+- the button controls the respective bulb (1) or has no effect on it (0),
+- the button is prssed(1) or not used (0).
-In addition, in the binary system $1+1=0$
-or also $2k=0$, $k\in\mathbb{Z}$, and simultaneously $1=-1$.
-In the case of light bulbs, this translates into following.
+In addition, in the binary system holds $1+1=0$, $1+0=1$,
+or equivalently $2k=0$, $2k+1=1$ for $k\in\mathbb{Z}$, and also $1=-1$. In the case of light bulbs, this translates into the following:
If we press the same button twice,
the corresponding bulb turns on and off (or vice versa).
-It goes back to its original state and it is the same,
+It goes back to its original state, and it is the same,
as if we hadn't pressed the button at all.
-The effect of each button on all bulbs can be written as a vector.
-Vectors $\textbf{a}$, $\textbf{b}$, $\textbf{c}$
-will describe the operation of buttons A, B, C respectively.
-Each coordinate of the vector describes the corresponding bulb in the
-corresponding order: first A, second B, third C. The designation 1
+The effect of each button on all bulbs can be represented by a vector. Vectors $\textbf{a}$, $\textbf{b}$, $\textbf{c}$
+will describe the effects of buttons A, B, C respectively.
+Each coordinate of a vector corresponds to the bulb in the given order: first coordinate - bulb A, second coordinate - bulb B, third coordinate – bulb C. The number 1 in a coordinate of a vector
means that the button changes the state of that bulb, and 0 means it
has no effect on it. According to the above button properties, the
-following applies
+following applies:
$$
\textbf{a}=\begin{bmatrix}1\\1\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\end{bmatrix},\quad
\textbf{c}=\begin{bmatrix}0\\1\\1\end{bmatrix}.
$$
-The vectors can also be used to describe actual state of bulbs.
-The bulb is on: 1, The bulb is of: 0.
-The initial state, when no bulb is on, would be described by the vector
+The vectors can also be used to describe the actual states of all bulbs. The bulb is lit: 1, or bulb is not lit: 0.
+The initial state, when no bulb is lit, is described by the vector:
$$
\textbf{s}=\begin{bmatrix}
0\\0\\0\end{bmatrix}.
$$
-By pushing buttons A and B subsequently, we got to the third picture.
-Written using vector addition in the binary system
-
+By pressing buttons A and B subsequently, we arrived at the state illustrated in the third picture.
+Using vectors, this can be expressed by vector addition with addition of coordinates done in the binary system.
$$
\textbf{s}+\textbf{a}+\textbf{b}=
\begin{bmatrix}0\\0\\0\end{bmatrix}+
@@ -97,26 +90,23 @@ $$
\begin{bmatrix}0\\0\\1\end{bmatrix}.
$$
-> **Exercise 1.** Determine the button combination,
->which must be pressed so that only bulbs A and C are on,
->when all three bulbs are initially off.
+> **Exercise 1.** Determine the button combination to light up bulbs A and C only, starting from the initial state where all three bulbs are off.
-*Solution.* The desired resulting state can be described by the vector
+*Solution.* The desired resulting state is described by the vector
$$
\textbf{t}=\begin{bmatrix}1\\0\\1\end{bmatrix}.
$$
-We solve the problem as a system of linear equations
+We solve the problem as a system of linear equations:
$$\textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} = \textbf{t},
$$
-where the coefficients ${\textbf{a}}$, ${\textbf{b}}$, ${\textbf{c}}$ describe,
-which bulbs are controlled by a given button, as mentioned above,
-and the variables $x_1, x_2, x_3$ take on the values 1 or 0, depending on
-whether we will use the relevant button or not.
-
-The first time, we will present the system including zero coefficients,
-to make clear how the vectors are rewritten into the system
-${\textbf{a}}$, ${\textbf{b}}$, ${\textbf{c}}$.
+where the vectors ${\textbf{a}}$, ${\textbf{b}}$, ${\textbf{c}}$ describe
+which bulbs are controlled by the respective buttons, as stated above,
+and the variables $x_1, x_2, x_3$ take values 1 or 0 depending on whether we use the corresponding button or not
+At first, we present the system including the zero coefficients,
+to make clear how the coordinates of the vectors
+${\textbf{a}}$, ${\textbf{b}}$, and ${\textbf{c}}$ are rewritten into the system.
+The system is:
$$
\begin{aligned}
0 + 1x_1 + 1x_2 + 0x_3 &= 1\\
@@ -125,7 +115,7 @@ $$
\end{aligned}
$$
-We solve the system, for example, using the substitution method:
+We solve the system, for instance, using the substitution method:
$$
\begin{alignat*}{3}
@@ -135,7 +125,7 @@ x_1 &+ x_2& &+ x_3&&= 0\\
\end{alignat*}
$$
-We substitute in the second equation:
+Substituting into the second equation:
$$
\begin{aligned}
@@ -145,45 +135,37 @@ x_2 &= 2,
\end{aligned}
$$
-but since we are working in a binary system where $2=0$, $x_2 = 0$
-holds. By substituting, we get $x_1=1, x_3=1$, which means that we
-have to press the A and C buttons to achieve the that bulbs A and C
-will be on and bulb B will be off.
+but in the binary system $2=0$, so $x_2 = 0$. Substituting back, we get $x_1=1, x_3=1$, meaning we have to press buttons A and C to achieve that bulbs A and C lit up while bulb B remains off.
-*Note.* The problems for three bulbs can be solved very easily
-off the top of the head, since each button is pressed at most once.
-Pressing more than once doesn't make sense
-because two presses of the same button come out the same as no press.
-In the following problem, we therefore increase the number of bulbs,
-but this will result in a set of more than three
+*Note.* The problems for three bulbs can be easily solved mentally since each button can be pressed at most once.
+Pressing the same button more than once doesn't make sense as pressing it twice yields the same result as not pressing it at all. In the following problem, we therefore increase the number of bulbs,
+but this will lead to a system of more than three
linear equations with more than three unknowns,
-which are probably no longer counted in regular mathematics classes.
-Therefore, the problems can be used in a special seminar,
+which is likely beyond the scope of typical mathematics classes.
+Therefore, these problems can be used in a special seminar
in which students are introduced to matrix calculus
-and can thus practise it on a specific word problem.
+and can thus practise it on specific word problems.
-> **Exercise 2.** We will expand the bulb network to five bulbs.
->The buttons still have the same property,
->they control the bulb above them and their immediate neighbours.
->At the beginning, not all the bulbs are off,
->but bulbs A and D are already on.
+> **Exercise 2.** We extend the bulb circuit to five bulbs.
+>The buttons still have the same property of controlling the bulb above them and its immediate neighbours.
+>Initially, not all the bulbs are off,
+>but bulbs A and D are already lit.
>
>
>
>Find out what combination of buttons to press to end up with
>- all the bulbs off,
->- only bulb E on.
+>- only bulb E remains lit.
-*Solution.* In addition to the number of linear equations
+*Solution.* Besides the number of linear equations
and variables in the system, the solution will also differ
-by a modified initial state,
-where all the bulbs are not in the 0 = off state.
-The initial state can be written as the vector
-
+ due to the modified initial state,
+where not all the bulbs are in the state 0 = off.
+The initial state can be represented by the vector
$$
\textbf{s} = \begin{bmatrix}1\\0\\0\\1\\0\end{bmatrix}
$$
-and the behaviour of buttons A to E is described by vectors
+and the behaviour of buttons A through E is described by vectors
$$
\textbf{a}=\begin{bmatrix}1\\1\\0\\0\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\\0\\0\end{bmatrix},\quad
\textbf{c}=\begin{bmatrix}0\\1\\1\\1\\0\end{bmatrix},\quad
@@ -216,42 +198,38 @@ $$
&& && && && && &x_4& &+& x_5 &=0
\end{alignat*}
$$
-When solving, remember that in a binary system, $-1=1$ and $2=0$.
-One of the equations will be reset to zero when we make adjustments,
-which would normally mean infinitely many solutions,
-but in finite calculus, this is not the case.
-The system has two solutions, which are vectors of order five
+While doing computations, remember that in the binary system $-1=1$ and $2=0$.
+When solving this system, one of the equations will result to have all coefficients zeros. If we were working in an infinite calculus, allowing computations with all real numbers, this system would have infinite number of solutions.
+<!-- "That normally means, that the system has infinitely many solutions." Tohle tvrzení je nepravdivé, matematicky špatně, proto ho vypouštím. -->
+However, in finite calculus, performing calculations in the binary system, this is not the case.
+Our system has exactly two solutions, which are the following two vectors of order five
$(0,1,1,0,0)$ a $(1,0,1,1,1)$.
-If only bulb E is to remain on, the following applies
+If only bulb E is to remain lit, the following vector represents the final state
$$
\textbf{t} = \begin{bmatrix}0\\0\\0\\0\\1\end{bmatrix}.
$$
After a few steps using the addition method or
-the Gaussian elimination method (when working with matrices)
-we would find that one of the equations of the system has no solution,
-and therefore the whole system has no solution for this problem.
-That is why we cannot change the bulbs from their original state
-where only A and D are on, to a state where bulb E alone is on.
-
-> **Exercise 3.** The new blue light bulbs differ from the previous ones in that,
->that they can glow in two different shades of blue.
->When this bulb is off, the first press of the button,
->which controls it, it will light up in light blue,
->the second press turns it dark blue and the third press turns it off again.
->The buttons still have the same property,
->that is, they control the bulb above them and their immediate neighbours.
->How many times you have to press which of the buttons A, B and C,
->to turn off all the bulbs from the state shown in the picture?
+the Gaussian elimination method (working with matrices)
+we would find that one of the equations of the system has no solution. Therefore, the whole system has no solution for this assignment.
+That is why we cannot turn the bulbs from their original state,
+where only A and D are lit, to the state where bulb E alone is lit.
+
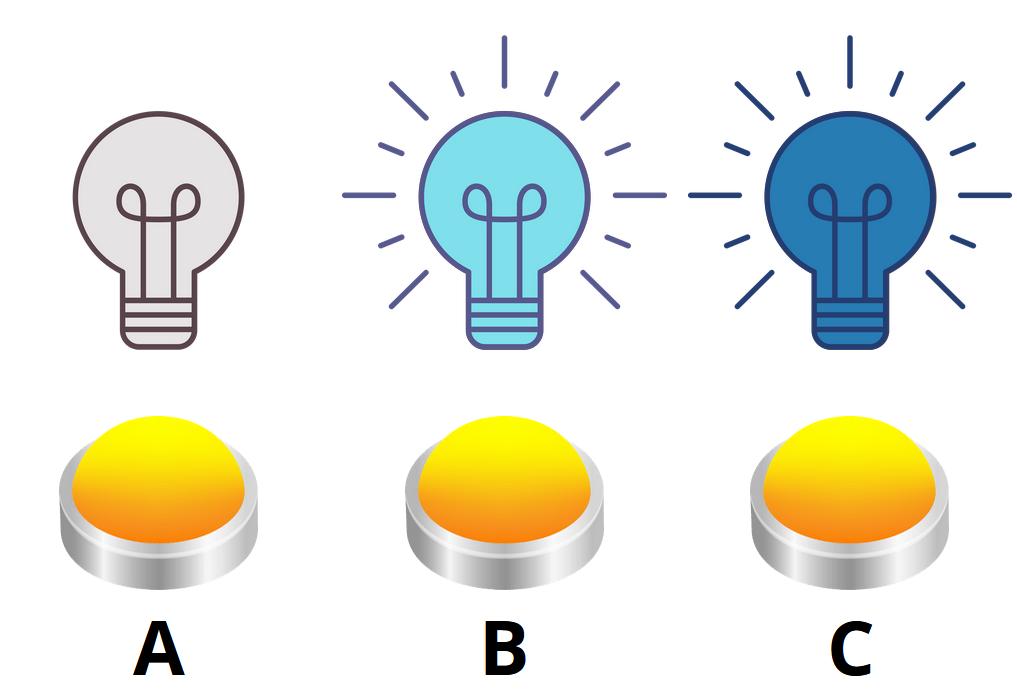
+> **Exercise 3.** In this exercise, the new, blue-glowing light bulbs differ from the previous ones in that
+> they can glow in two different shades of blue.
+>When such bulb is off, the first press of the button,
+>which controls it, will make it glow in light blue,
+>the second press in dark blue, and the third press turns it off again.
+>The buttons still have the same property of controlling the bulb above them and its immediate neighbours.
+>How many times and which of the buttons A, B and C, do you have to press
+>to turn off all the bulbs from the initial state shown in the picture?
> 
+*Solution.* Because the bulbs now have three states
+they can be in, we switch to counting
+in the ternary system. Let's denote the bulb "is off" = 0,
+"glows light blue" = 1, and "glows dark blue" = 2.
-*Solution.* Because the bulbs now have three states,
-they can be in, we move on to counting in
-in a ternary system. Let's denote the bulb "not lit" = 0,
-"glows light blue" = 1 and "glows dark blue" = 2.
-
-However, buttons A, B, C can only control the given bulb,
-or not to control, there is no third option, so the same still apply
+However, buttons A, B, C can still only control the given bulb, or not control it. There is no a third option, so still the same applies
$$
\textbf{a}=\begin{bmatrix}1\\1\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\end{bmatrix},\quad
@@ -259,18 +237,18 @@ $$
$$
For the initial state ${\textbf{s}}$ and
-the desired final state ${\textbf{t}}$ the following applies
+the desired final state ${\textbf{t}}$ the following holds true
$$
\textbf{s} = \begin{bmatrix}0\\1\\2\end{bmatrix}, \quad \textbf{t} = \begin{bmatrix}0\\0\\0\end{bmatrix}.
$$
-According to the previous we have
+According to the above notation we have
$$
\textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} = \textbf{t},
$$
-and we can write down a system of three linear equations
+and we can set up a system of three linear equations
$$
\begin{aligned}
0 + 1x_1 + 1x_2 + 0x_3 &= 0\\
@@ -278,7 +256,7 @@ $$
2 + 0x_1 + 1x_2 + 1x_3 &= 0
\end{aligned}
$$
-and we will solve it.
+and solve it.
$$
\begin{aligned}
x_1 &+ x_2& && &= 0 \\
@@ -286,7 +264,7 @@ x_1 &+ x_2& &+ x_3&&= -1\\
&& x_2 &+ x_3&&= -2
\end{aligned}
$$
-From the first and third lines we express $x_1$ and $x_3$ depending on $x_2$
+From the first and third row we express $x_1$ and $x_3$ in terms of $x_2$
$$
\begin{aligned}
x_1 &= -x_2\\
@@ -301,10 +279,8 @@ $$
x_2 &= -1.
\end{aligned}
$$
-In the ternary system holds $3k=0$, $k\in\mathbb{Z}$,
-$3l+1=1$, $l\in\mathbb{Z}$ and $3m+2=2$, $m\in\mathbb{Z}$, therefore $-1=2$ or
-also $-2=1$, and therefore $x_2 = 2$, $x_1 = -2 = 1$ a $x_3 = -1 = 2$.
+In the ternary system $3k=0$, $k\in\mathbb{Z}$,
+$3l+1=1$, $l\in\mathbb{Z}$, and $3m+2=2$, $m\in\mathbb{Z}$, so $-1=2$ and $-2=1$, and therefore $x_2 = 2$, $x_1 = -2 = 1$, and $x_3 = -1 = 2$.
-The result is that once we press the A button, button B twice and
-button C twice, from the original state in the picture, all the bulbs
-go off.
+As a result, by pressing button A once, button B twice, and
+button C twice, we turn off all the bulbs from the original state shown in the picture.