diff --git a/00013_Golf_ball/en_article_proofreading.md b/00013_Golf_ball/en_article_proofreading.md
index 3b6100b..45569ba 100644
--- a/00013_Golf_ball/en_article_proofreading.md
+++ b/00013_Golf_ball/en_article_proofreading.md
@@ -3,135 +3,140 @@ keywords:
- optimalization
- quadratic equation
- derivation
-is_finished: False
+is_finished: True
---
+% Pozor, oprava provedena pouze v en_article
+
# The launch of the ball
## Oblique launch
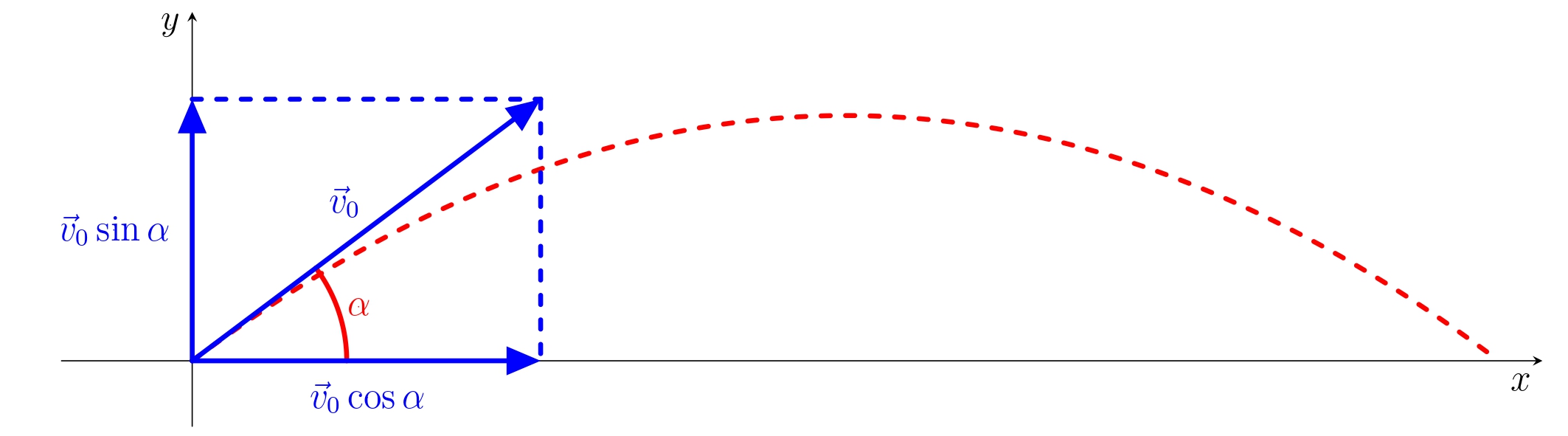
The oblique launch is the most general way of setting a object in a
-homogeneous gravitational field into motion. Suppose that a point of
-mass has been thrown obliquely in space without resistance and the
-vector of its initial velocity $v_0$ coincides with the horizontal
-plane at an angle $\alpha$. WWhen introducing the Cartesian coordinate
-of the system with the $x$ axis horizontal in the direction of the
-throw and the $y$ axis vertical upwards the velocity will be given by
-the vector
+homogeneous gravitational field into motion. Suppose that a body
+(point mass) has been thrown obliquely in space without
+resistance. The initial velocity is $\vec{v}_0$ and the angle between
+and the vector $\vec{v}_0$ and horizontal direction is
+$\alpha$. Introduce the Cartesian coordinate system with horizontal
+$x$-axis and vertical $y$-axis as on the picture. The coordinates of
+the initial velocity vector are
$$\vec{v}_0=(v_0\cos\alpha,v_0\sin\alpha).$$
-The motion of the object is affected by an acceleration of gravity $g$
-directed vertically downwards. The horizontal component of the
-gravitational acceleration is zero and therefore in the horizontal
-direction the motion is unaffected by the gravitational field. In
-vertical direction, the velocity of the object is affected by the
-acceleration $-g$ and is uniformly decelerated motion.
-
-For the coordinates of the mass point it will be valid
+The motion of the body is governed by an acceleration of gravity $g$
+directed vertically downwards. The horizontal component of the
+gravitational acceleration is zero. Therefore the motion in the
+horizontal direction is unaffected by the gravitational field and the
+horizontal component of the motion is a motion with constant
+speed. The vertical component of the motion is affected by the
+negative acceleration $-g$ and it is a movement with constant
+acceleration and initial velocity $v_0t\sin\alpha$ (an uniformly
+decelerated motion).
+
+For the coordinates of the body we can use formulas for distance
+of motion with constant speed and constant acceleration an get
$$
\begin{aligned}
x(t) &= v_0 t\cos\alpha,\\
y(t) &= v_0t\sin\alpha-\frac{1}{2}gt^2.
-\end{aligned}
+\end{aligned}\tag{1}
$$
-
+
-## Maximum distance launch
+## Motion of golf ball
-A golfer hits the ball with an initial velocity $v_0$ forming with the
-horizontal plane an angle $\alpha$. Let's assume it acts on the ball
-negligible resistance forces. The motion of the ball therefore
-satisfies the conditions for movement of an obliquely thrown body in
-an environment without air resistance.
+A golfer hits the ball with an initial velocity $v_0$. The angle
+between the initial velocity and the horizontal plane is
+$\alpha$. Let's assume that drag forces are negligible. The motion of
+the ball therefore satisfies the conditions for movement of an
+obliquely thrown body in an environment without air resistance.
>**Exercise 1.** Prove that the trajectory of a golf ball is a parabola.
-*Solution.* To find the equation of the trajectory, that is the
-function $y=f(x)$, it is necessary to remove the parameter $t$ from
-the equations determining the position of the point:
-$$
-\begin{aligned}
- x(t) &= v_0 t\cos\alpha,\\
- y(t) &= v_0t\sin\alpha-\frac{1}{2}gt^2.
-\end{aligned}
-$$
+*Solution.* To find the equation of the trajectory in the form
+$y=f(x)$ it is necessary to eliminate the parameter $t$ from
+the system (1).
-Therefore, we express from the first equation the time
-$t=\frac{x}{v_0\cos\alpha}$ and we substitute it into the second
-equation:
+We solve the first equation with respect to time
+$t=\frac{x}{v_0\cos\alpha}$
+and substitute into the second equation:
$$y(x) = v_0\sin\alpha\,\frac{x}{v_0\cos\alpha} -\frac{1}{2}g\frac{x^2}{v_0^2\cos^2\alpha}= -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .$$
From here we see that the $y$-coordinate of the trajectory is a
quadratic function of the $x$-coordinate and the trajectory of the
-golf ball is therefore a parabola.
+golf ball is a parabola.
->**Exercise 2.** Calculate the height of the throw, i.e. the maximum
+>**Exercise 2.** Calculate the height of the throw, i.e. the maximal
>height $y_{max}$ that the launched ball reaches.
-*Solution.* To calculate the height of the throw, we need to calculate
-the extremum of the function from the previous point:
+*Solution.* The height of the throw is the maximum of the function
+from the previous exercise:
$$f\colon y = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .$$
+
We calculate the derivative of the function $f$ as
$$
-y'=-\frac{g}{2v_0^2\cos^2\alpha}\cdot2x+\frac{\sin\alpha}{\cos\alpha}\ .
+y'=-\frac{g}{2v_0^2\cos^2\alpha}\cdot2x+\frac{\sin\alpha}{\cos\alpha}.
$$
+
To find the stationary point, we set the derivative equal to zero and
-we get the equation
+obtain the equation
$$
\frac{g}{v_0^2\cos^2\alpha}\cdot x=\frac{\sin\alpha}{\cos\alpha}\ .
$$
-Its solution is
+The solution of this equation is
$$
x_{max}=\frac{v_0^2\sin\alpha\cos\alpha}{g}\ .
$$
-Since the trajectory of motion is a concave quadratic function,
-the located stationary point must be its maximum, i.e. the height of the throw.
-The height of the throw is calculated by inserting the obtained
-coordinate $x_{max}$ to the function $f$:
+Since the trajectory of motion is a quadratic function with vertex up,
+the located stationary point must be a maximum. The $y$-coordiante of
+the stationary point is the height of the throw.
+
+The height of the throw is calculated by evaluating the function $f$
+at the obtained coordinate $x_{max}$:
$$y_{max}=\frac{v_0^2\sin^2\alpha}{2g}\ .$$
-> **Exercise 3.** Calculate at what angle $\alpha$ will fly
-> ball at a constant initial velocity to
-> maximum distance $x_{d}.$
+> **Exercise 3.** Given constant initial velocity, find the angle
+> $\alpha$ which guaranties maximal distance between the initial and
+> the terminal point on the trajectory.
-*Solution.* To calculate the maximum range angle
-we need to obtain the function of the $x$ coordinate depending on the angle
-$\alpha$, i.e. the function $x(\alpha).$ Given that $y=0$ when
-the ball hits a ground, we substitute in the function
-$$y(x) = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x$$
-for $y$ zero height and we derive $x(\alpha):$
+*Solution.* To find the maximum range angle we need to obtain the
+terminal point $x_d$ of the trajectory as a function of the angle
+$\alpha$ and find the maximum of the function $x_d(\alpha).$ Given
+that $y=0$ when the ball hits a ground, we find zeros of the function
+$$y(x) = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x.$$
+From here we obtain:
$$0 = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ ,$$
$$0 = x\cdot\left(-\frac{g}{2v_0^2\cos^2\alpha}\cdot x+\frac{\sin\alpha}{\cos\alpha}\right)\ .$$
-This equation in product form has two solutions. The first solution
+This factorized equation has two solutions. The first solution
$x=0$ corresponds to the place where the ball is launched and the
second solution $x_d$ to the place of impact
$$x_d(\alpha) = \frac{2v_0^2\sin\alpha\cos\alpha}{g}=\frac{v_0^2}{g}\sin2\alpha\ .$$
-Now we need to find the maximum of the function $x_d(\alpha)$, i.e.
-find its stationary point. We calculate the derivative of the function
-$x_d(\alpha)$ by $\alpha$
+Now we need to find the maximum of the function $x_d(\alpha)$. It is
+sufficient to find the stationary point, since it has been showed that
+the trajectory is a parabola with vertex up. We calculate the
+derivative of the function $x_d(\alpha)$ by $\alpha$
$$x_d'(\alpha)=\frac{v_0^2}{g}\cdot\cos2\alpha\cdot 2\ .$$
-If we set the derivative equal to zero, we get for stationary point
+Letting the derivative equal to zero, we get
$\cos2\alpha=0$, which is satisfied for $2\alpha=90^\circ$ (for the
ball to be launched, obviously
$\alpha\in\langle0^\circ,90^\circ\rangle$, so the solution is
-unambiguous).
-
-The maximum range in golf is achieved when hitting the ball at an angle
-$\alpha=45^\circ$ and the ball lands at a distance of
-$$x_d(45^\circ) =\frac{v_0^2}{g}\sin(2\cdot45^\circ)=\frac{v_0^2}{g}\ .$$
-
-We could have obtained the function $x_d(\alpha) =
-\frac{v_0^2}{g}\sin2\alpha$ more easily by using the symmetry of the
-parabola. This is because the vertex of the parabola lies in the
-middle of the trajectory of the ball. Therefore, for the x-coordinate
-of the vertex holds $x_d(\alpha) = 2\cdot x_{max}$. This avoids
-computing the product equation obtained by substituting $y=0$ into the
-function $y(x)$.
+unambiguous). Thus the stationary point is $\alpha=45^\circ$.
+
+The maximum range in golf is achieved when hitting the ball at an
+angle $\alpha=45^\circ$ and the ball lands at a distance of
+$$x_d(45^\circ) =\frac{v_0^2}{g}\sin(2\cdot45^\circ)=\frac{v_0^2}{g}.$$
+
+Note that it is possible to obtain the function $x_d(\alpha) =
+\frac{v_0^2}{g}\sin2\alpha$ without calculus by using the symmetry of the
+parabola. The vertex of the parabola is located in the
+middle of the zeros. Therefore, for the $x$-coordinate
+of the impact point can be evaluated as $x_d(\alpha) = 2\cdot x_{max}$. This avoids
+solving the quadratic equation obtained by substituting $y=0$ into the
+function $y(x)$ and factorizing the right-hand side.
## Literature