diff --git a/00012_Optimalization_Merry_go_round/en_article_proofreading.md b/00012_Optimalization_Merry_go_round/en_article_proofreading.md
index e2ef822..39de62d 100644
--- a/00012_Optimalization_Merry_go_round/en_article_proofreading.md
+++ b/00012_Optimalization_Merry_go_round/en_article_proofreading.md
@@ -1,99 +1,96 @@
---
keywords:
-- optimalization
+- optimization
- quadratic equation
- floor function
is_finished: False
---
-# Optimal ticket price
+# Optimal Ticket Price
-The carousel owner wants to set the ticket price for his attraction so that his profit is maximized.
+The carousel owner wants to set the ticket price for his attraction so that his profit is maximized.
For simplicity, he sets the entry fee in multiples of 10 CZK.
He knows that at the current price of 50 CZK, he can expect about 600 visitors per day.
-From previous years, he estimates that if the ticket price increases by 10 CZK, about 50 fewer visitors will come per day,
-while if the ticket price drops by 10 CZK, 50 more visitors will come.
-To increase the visitor interest, every third visitor will receive cotton candy worth 30 CZK on the account of the carousel owner.
+From previous years, he estimates that if the ticket price increases by 10 CZK, about 50 fewer visitors will come per day. Conversely, if the ticket price drops by 10 CZK, 50 more visitors will come.
+Additionally, to increase visitor interest, every third visitor will receive cotton candy worth 30 CZK at the carousel owner’s expense.
-Since the son of the carousel owner happens to be studying mathematics, he decides to help his father with the problem.
+Since the son of the carousel owner happens to be studying mathematics, he decides to help his father with this problem.
>**Exercise 1.** After some thought, the son wrote the formula
>$$ y= (50+10x)\cdot (600-50x) - \frac{600-50x}{3}\cdot 30.$$
->Decode the individual parts of this formula.
+>Interpret the individual parts of this formula.
-*Solution.* The following table explains the role of each part ot the formula:
+*Solution.* The following table explains the meaning of each part of the formula:
-| Part of the formula | Significance |
+| Part of the Formula | Meaning |
| ------------- | ------------- |
| $10x$ | change in ticket price by $x\cdot 10\ \text{CZK}$ |
| $50+10x$ | new ticket price |
| $600-50x$ | estimated number of visitors after price change |
| $(50+10x)(600-50x)$ | daily ticket earnings |
-| $\frac{600-50x}{3}$ | number of visitors in one day |
+| $\frac{600-50x}{3}$ | number of visitors receiving cotton candy |
| $\frac{600-50x}{3}\cdot 30$ | daily cost of cotton candy |
| $y$ | total daily profit |
->**Exercise 2.** If we understand the previous formula as a function of the variable $x$,
->what function is it and what does its graph look like?
+>**Exercise 2.** If we consider the previous formula as a function of the variable $x$,
+>what type of function is it and what does its graph look like?
-*Solution.* By editing the right side of the formula, we convert it to the form
+*Solution.* By simplifying the right side of the formula, we convert it to the form
$$y=-500x^2+4\ 000x+24\ 000\ .$$
-This gives us a quadratic function whose graph is a parabola.
-This parabola is concave because of the negative coefficient of the quadratic term.
+This is a quadratic function whose graph is a parabola.
+Due to the negative coefficient of the quadratic term, this parabola is concave down. <!-- mohlo by být také “this parabola opens downward” -->
+<!-- V anglické terminologii se používá dvojí názvosloví (“concave = konkávní” a “convex = konvexní”, ale častěji, což je pro studenty srozumitelnější, se používá “concave up = konvexní” a “concave down = konkávní”. Doporučuji tady použít “concave down” což je jednoznačně vystihující tvar paraboly ať už je čtenář zvyklý na kterékoli z uvedených názvosloví)-->
>**Exercise 3.** At what ticket price would the owner make the maximum profit?
*Solution.* Our task is to determine the maximum of the function
-$$f\colon y=-500x^2+4\ 000x+24\ 000\ .$$
+$$f(x)=-500x^2+4\ 000x+24\ 000\ .$$
+<!-- Zápis "f: y =" je pro anglické matematické texty nestandardní. Myslím, že můžeme rovnou funkci zapsat "f(x)= " a podobně u funkce g "g(x) = ".-->
We know that the graph of the function $f$ intersects the $x$-axis at points corresponding to the roots of the quadratic polynomial.
-At the centre of the line segment joining these points, we can find the maximum of the function we are looking for (as implied by the symmetry of the parabola).
-Therefore we determine the roots of the quadratic polynomial.
+At the midpoint of the line segment joining these points, we can find the maximum of the function we are looking for (due to the symmetry of the parabola).
+Therefore, we determine the roots of the quadratic polynomial.
$$\begin{aligned}
-500x^2 + 4\,000x + 24\,000 &= 0 \\
x^2 - 8x - 48 &= 0\\
(x-12)(x+4)&=0
\end{aligned}$$
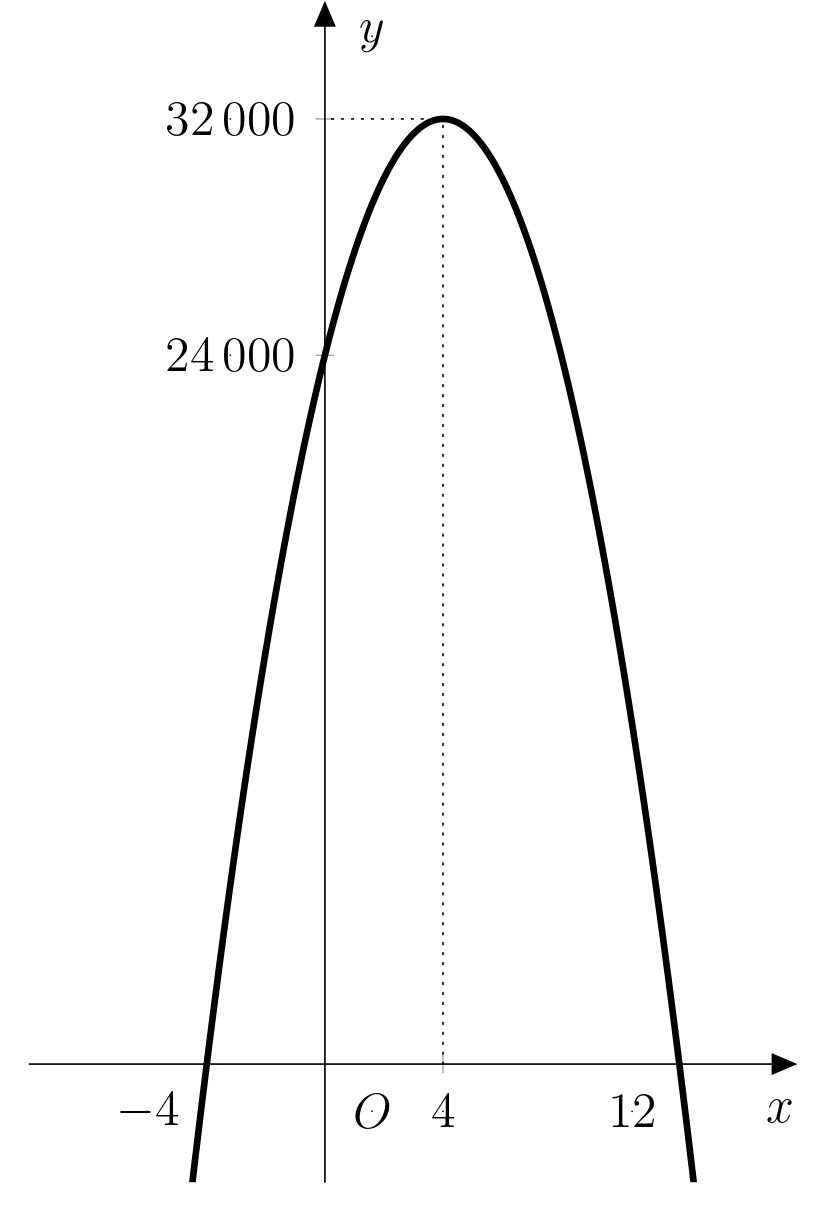
The solutions of the equation are the roots $x_1=12$ and $x_2=-4$, so the maximum of the function $f$ is at the point $x_{max}=\frac{12-4}{2}=4$.
-We have thus increased the original ticket price by $40$ to a new price of $90\ \text{CZK}$.
+We have thus increased the original ticket price by $40$ to a new price of $90\ \text{CZK}$ to achieve the maximum profit.
->**Exercise 4.** How much is the maximum profit greater than the profit at the original price?
+>**Exercise 4.** How much is the maximum profit greater than the profit at the original ticket price?
*Solution.* The answer to this problem is the difference $f(4)-f(0)$.
-By successively substituting both values into the prescription of the $f$ function, we get $f(4)=32 000$
-and $f(0)=24 000$. The difference between the two amounts is then equal to $8 000\ \text{CZK}$.
-The graph of the function $f$ with marked values $f(4)$ and $f(0)$ is shown in the figure:
+By substituting both values into the function $f$, we get $f(4)=32 000$ <!--Termín “perscription” nelze použít ve významu “předpis funkce”. Je to třeba předpis na léky. Pro “předpis funkce” lze použít “equation (formula) of the function” nebo stačí jen “function” v tomto případě. -->and $f(0)=24 000$. The difference between the two amounts is $8 000\ \text{CZK}$.
+The graph of the function $f$ with the values $f(4)$ and $f(0)$ marked is shown in the figure:
-
+
>**Exercise 5.** When creating the formula, the son simplified one aspect of the problem.
>Do you know which one? Could you solve the problem without this simplification?
->Compare your model with the one that son of the carousel owner created.
+>Compare your model with the one created by the son of the carousel owner.
*Solution.* The son's formula is accurate only if the
-number of visitors per day $600-50x$ is divisible by three. If it is not divisible by three, then the number of gifted visitors is equal to
-the lower integer part of the number $\frac{600-50x}{3}$; we denote $\left\lfloor\frac{600-50x}{3}\right\rfloor$.
+number of visitors per day $600-50x$ is divisible by three. If it is not divisible by three, then the number of visitors who received the gift is
+the lower integer part of the number $\frac{600-50x}{3}$, denoted as $\left\lfloor\frac{600-50x}{3}\right\rfloor$.
The function that takes as input a real number $x$
and gives as output the greatest integer $m$ such that $m\leq x$ is called *the floor function*.
-For example $\left\lfloor \frac{5}{2}\right\rfloor = 2$, $\left\lfloor
+For example, $\left\lfloor \frac{5}{2}\right\rfloor = 2$, $\left\lfloor
\pi\right\rfloor = 3$ nebo $\left\lfloor -8{,}3\right\rfloor = -9$.
-Now let's compare the previously used function $f$ with the new floor function $g$, which
-calculates the lower integer part:
+Now, let's compare the previously used function $f$ with the new function $g$, which <!--funkce g není “flor function”. Jen ji používá. -->
+uses the lower integer part:
$$
-g\colon y = (50+10x)\cdot (600-50x) - \left\lfloor\frac{600-50x}{3}\right\rfloor\cdot 30.
+g(x) = (50+10x)\cdot (600-50x) - \left\lfloor\frac{600-50x}{3}\right\rfloor\cdot 30.
$$
$x_{max}=4$.
-We will make the comparison for the neighborhood of the already determined maximum $x_{max}=4$.
-For $x$ we will thus substitute meaningful values from the interval $\langle
-3{,}5;4{,}5 \rangle$, while we consider meaningful such values,
-so that both the ticket price and the number of visitors are integers. It can be seen
-that it is enough to focus on the whole number of the ticket price,
-and it will be integer for just such values,
-which have at most one decimal place in decimal notation.
+ We will compare the results around the already determined maximum, $x_{max}=4$.
+For $x$, we will substitute values from the interval $\langle
+3{,}5;4{,}5 \rangle$, considering values for which both the ticket price and the number of visitors are integers. It can be observed
+that it is sufficient to ensure that the ticket price is an integer, which will occur for values of $x$ with at most one decimal place. <!-- věta významově neodpovídala -->
-The results of the function evaluations can be summarized in a table
-(it is preferable to use MS Excel type of software for calculations):
+The functions values can be summarized in a table
+(it is advantageous to use software like MS Excel for calculations):
$$
\begin{array}{c|ccccccccccc}
@@ -104,22 +101,22 @@ g(x) & 31\,895 & 31\,920 & 31\,965 & 32\,000 & 31\,995 & 32\,010 & 32\,015 & 31\
$$
The daily profit determined by the function $g$ is always greater than or equal to the daily profit
-determined by function $f$. Also, the maximum of the function $g$ is at a different point,
-which is $4{,}1$, which corresponds to a ticket price of $91\ \text{CZK}$
+determined by the function $f$. Also, the maximum of the function $g$ is at a different point,
+specifically $4{,}1$, which corresponds to a ticket price of $91\ \text{CZK}$
and an estimated daily attendance of 395 people.
-We can notice the following facts:
+We can observe the following facts:
-- The differences between the profits are very small, in fractions of the price of a single ticket.
+- The differences between the profits are very small, within fractions of the price of a single ticket.
It doesn't matter whether the ticket costs 90 or 91 CZK, because
the only person who comes in extra (or doesn't come in) compared to the estimates,
reliably erases any difference between the profits of the two models.
- While we determine the maximum of the function $f$ by a direct and relatively simple calculation,
we had to determine the maximum of the function $g$ by substituting all of the
-permissible values (and from a relatively narrow interval).
+permissible values (from a relatively narrow interval).
-Therefore, it can be said that despite the simplification, it is sufficient (and in fact
-more convenient) to use the function $f$ to calculate the maximum profit.
+Therefore, despite the simplification, using the function $f$ to calculate the maximum profit is both sufficient and more convenient.
+